在职位招聘数据处理中使用Loess回归曲线以及分箱、回归、聚类方法 检查离群点及光滑数据【数据挖掘&机器学习】

一.需求分析

本文主题：使用局部回归（Loess）曲线（增加一条光滑曲线到散布图）方法处理数据以及使用分箱、回归、聚类方法 检查离群点及光滑数据；

前文回顾，我们上篇文章写了招聘网站的职位招聘数据的分位数图、分位数-分位数图以及散点图、使用线性回归算法拟合散点图处理。之前的文章我们已经对爬取的数据做了清洗处理，然后又对其数据做了一个薪资数据的倾斜情况以及盒图离群点的探究。

我们到了现在对机器学习已经是做了很多的工作了。

我们这次的任务需求是：

使用局部回归（Loess）曲线（增加一条光滑曲线到散布图）方法处理数据 使用分箱、回归、聚类方法 检查离群点及光滑数据；

二.使用局部回归（Loess）曲线（增加一条光滑曲线到散布图）方法处理数据

Loess：

局部加权回归是一种非参数学习算法，它使我们不必太担心自变量的最高阶项的选择 我们知道，对于普通线性回归算法，我们希望通过以下方式预测x点的y值：

我们现实生活中的许多数据可能无法用线性模型来描述。这仍然是一个房价问题。显然，直线不能很好地拟合所有数据点，误差非常大，但类似于二次函数的曲线可以很好地吻合。为了解决为非线性模型建立线性模型的问题，当我们预测一个点的值时，我们选择接近该点的点，而不是所有点进行线性回归。在此基础上，提出了一种局部加权线性回归算法。在这个算法中，其他人越接近一个点，权重越大，他们对回归系数的贡献越大。

公式为：

1.第一步都是老规矩了，先读取我们的目标文件，然后，我们使用关键词“java”对数据进行筛选，循环筛选过程中将职位名，薪资需要的关键字放到列表里面，然后存入字典里，经过pandas的处理：

事前准备：将需要的包引入：

import re
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import mpl

指定默认字体：解决plot不能显示中文问题,解决保存图像是负号’-'显示为方块的问题

mpl.rcParams['font.sans-serif'] = ['STZhongsong']    
mpl.rcParams['axes.unicode_minus'] = False           

使用关键词“java”对数据进行筛选：

xingzhi={}
zhiwei = []
xin1 = []
xin2 =[]
for i in range(len(data)):
    if "java" in data.iloc[i]['职位名']:
        a = re.findall("\d+.?\d*", data.iloc[i]['薪资'])
        # print(data.iloc[i]['职位名'])
        zhiwei.append(data.iloc[i]['职位名'])
        xin1.append(int(a[0]))
        xin2.append(int(a[1]))
xingzhi={"职位名":zhiwei,'最低薪资':xin1,'最高薪资':xin2}
df = pd.DataFrame(xingzhi)
java1=xin1
java2=xin2

2.使用lowess函数，先对数据集进行一个排序，然后传入lowess函数进行一个计算，得到的数据进行一个绘图：

import numpy as np
import statsmodels.api as sm
lowess = sm.nonparametric.lowess
import pylab as pl
​
yest = lowess(np.sort(java1),np.sort(java2), frac=0.01)[:,0]
print(yest)
print(java1.sort)
pl.clf()
plt.scatter(java1,java2, c="red", marker='o', label='java')
pl.plot(np.sort(java1), yest, label='y pred')
plt.xlabel('Java岗位薪资下限')
plt.ylabel('Java岗位薪资上限')
pl.legend()
plt.show()

3. 效果图

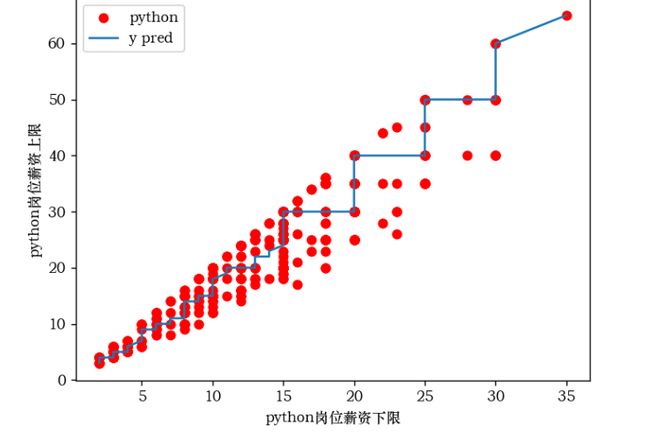
Java岗位薪资的的下限和上限的局部回归（Loess）曲线：

Go岗位薪资的的下限和上限的局部回归（Loess）曲线

python岗位薪资的的下限和上限的局部回归（Loess）曲线

三.使用分箱、回归、聚类方法 检查离群点及光滑数据；

为什么要分箱：

1.在盒分裂离散化之后，变量的容忍度增强，异常值对模型的影响将很小。例如，平均消耗量为1000，当一个样本的消耗量为10000时，可以忽略对模型的干扰 2.它具有很强的稳定性。

例如，一个样本现在是22岁，明年是23岁，一个盒子一个盒子的划分在[20，30]的范围内。虽然样本的年龄发生了变化，但仍在原始的盒划分范围内 3.离散化后，变量的值减小，可以减少模型的过拟合；例如，盒子分割前的值为1-10。如果每个值为1个盒子，则有10个盒子，模型将过度学习；如果将模型分为四个框，则模型不会过度学习所有变量的信息 4.盒离散化可以将缺失的值作为一个独立的盒，并将缺失的信息集成到模型中 5.变量装箱也是数据标准化处理的一种方式，它可以将不同尺度的所有变量转换为同一尺度，避免模型给大尺度变量太多权重

1.与上文一样，我们使用关键词“java”对数据进行筛选，循环筛选过程中将职位名，薪资需要的关键字放到列表里面，然后存入字典里，经过pandas的处理： 将上限和下限分别处理：

xingzhi={}
zhiwei = []
xin1 = []
xin2 =[]
for i in range(len(data)):
    if "java" in data.iloc[i]['职位名']:
        a = re.findall("\d+.?\d*", data.iloc[i]['薪资'])
        # print(data.iloc[i]['职位名'])
        zhiwei.append(data.iloc[i]['职位名'])
        xin1.append(int(a[0]))
        xin2.append(int(a[1]))
xingzhi={"职位名":zhiwei,'最低薪资':xin1,'最高薪资':xin2}
df = pd.DataFrame(xingzhi)
java1=xin1
java2=xin2

2.引入分箱、回归、聚类方法的一些模块包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

3.构建数据集

X = np.reshape(java1,(-1, 1))
y = np.reshape(java2,(-1, 1))
X = (np.sort(X))
y = (np.sort(y))

4.用KBinsDiscretizer转换数据集

enc = KBinsDiscretizer(n_bins=50, encode='ordinal', strategy='uniform')
X_binned = enc.fit_transform(X)

‘ordinal’：返回编码为整数值的 bin 标识符。

5.用原始数据集进行预测

fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = X
reg1 = LinearRegression().fit(X, y)
ax1.plot(line, reg1.predict(line), linewidth=2, color='green',
         label="线性回归")
print(line)
print("reg.predict(line)::",reg1.predict(line))
reg = DecisionTreeRegressor().fit(X, y)
ax1.plot(X, reg.predict(y), linewidth=2, color='red',
         label="决策树")
ax1.plot(X, y, 'o', c='k')
ax1.legend(loc="best")
ax1.set_ylabel("Java薪资上限")
ax1.set_xlabel("Java薪资下限")
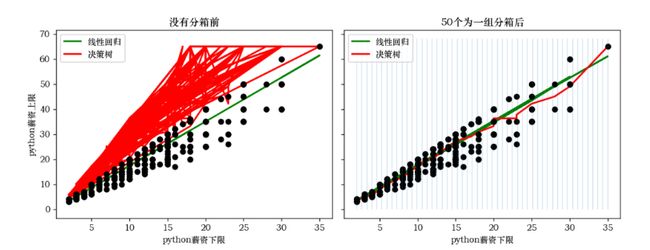
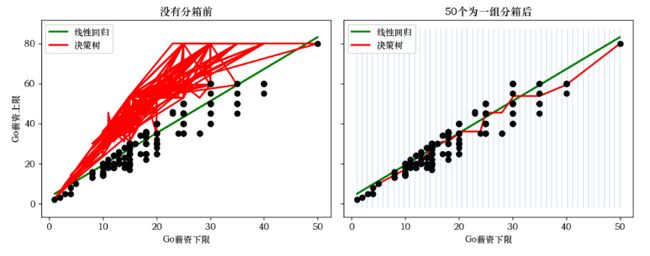
ax1.set_title("没有分箱前")

6.用转换后的数据进行预测

line_binned = enc.transform(X)
# print("line::",line)
# print("line_binned::",line_binned)
reg = LinearRegression().fit(X_binned, y)
a=reg.predict(line_binned)
ax2.plot(line,reg.predict(line_binned), linewidth=2, color='green',
          label='线性回归')
print(line)
print(a[a[:, 0].argsort()])
print(reg.predict(line_binned))
print(type(a))
reg = DecisionTreeRegressor(min_samples_split=3,
                            random_state=0).fit(X_binned, y)
ax2.plot(np.sort(java1), np.sort(reg.predict(line_binned)), linewidth=2, color='red',
         linestyle='-', label='决策树')
ax2.plot(X, y, 'o', c='k')
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=.2)
ax2.legend(loc="best")
ax2.set_xlabel("Java薪资下限")
ax2.set_title("50个为一组分箱后")
plt.tight_layout()
plt.show()

7.效果图：

Java岗位薪资的的下限和上限的分箱、回归、聚类结果图

Python岗位薪资的的下限和上限的分箱、回归、聚类结果图

Go岗位薪资的的下限和上限的分箱、回归、聚类结果图

本次总结：

对python数据的操作又有了很高程度的提升，对数据处理工具kettle的使用也加深了熟练度，对数据预处理技术也有了很深的理解和运用，后面我对之前机器学习的一些算法也进行了较为深入的复习和实战，后面我又帮助了小组的成员解决他们遇到的问题，对数据可视化也起到了复习的作用，而且我全程还使用gitee来管理项目代码，虽然小组成员对git操作较为陌生，但是随着大家项目的推进，大家也是耳濡目染了一些git的基本操作。 本次让我有了一定对数据处理和机器学习以至于对后面深度学习的一些兴趣，同时也认识到了这个方向的难度，和自己掌握的内容不过是冰山一角，后续我会对其进行一个模块化的深入学习。