ViT总结
Vision Transformer
文章目录
- Vision Transformer
-
- 总体结构
-
- 模型工作流程概述
- 图中需要注意的部分
-
- 左图
- 右图
- 代码实现
-
- 图片patch化
-
- 代码逻辑
- 代码实现
- Patch+Position Embedding
-
- 代码逻辑
- 代码实现
- Transformer Encoder
-
- 输入
- Norm层
-
- 代码逻辑
- 代码实现
- Mutil-Head Attention层
-
- 注意力机制(为了引出多头注意力机制)
-
- 代码逻辑
- 数学表达
- 多头注意力机制(模型中实际使用到的)
-
- 代码逻辑
- 代码实现
- MLP层
-
- 代码逻辑
- 代码实现
- ViT整体架构(基于上述结构)
- 模型分类效果
-
- MNist
-
- 训练参数
- 分类效果
- cifar-10
-
- 训练参数
- 分类效果
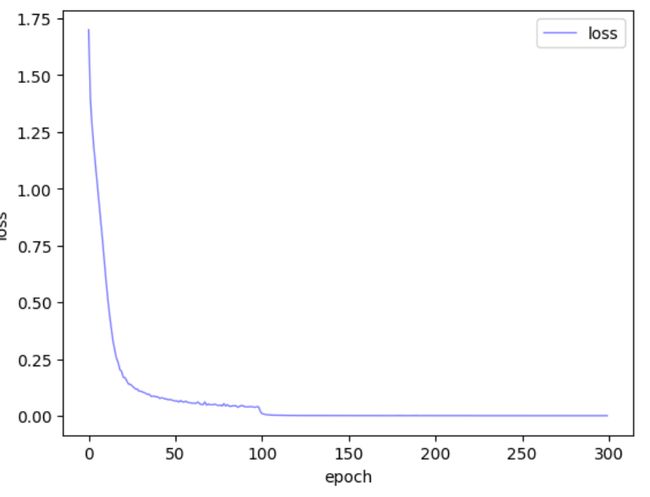
- 训练时loss变化
ViT是自然语言处理中transformer在计算机视觉中的应用,ViT在计算机视觉应用中取得了显著的成果,模糊了自然语言处理与计算机视觉之间的界限。在ViT中最重要的结构是Transformer Encoder。这其中最重要的部分是注意力机制。ViT通过Transformer将图像的特征信息整合在一个向量中,并基于此进行分类任务。
总体结构
下图是ViT的结构图,以及ViT模型工作的原理图。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Us9pz4a7-1667396655967)(https://cdn.jsdelivr.net/gh/wenruo-shusheng/BlogImageBed@main/img/ViT%E6%A6%82%E5%BF%B5%E5%9B%BE.png)]
模型工作流程概述
ViT可以被用于多分类问题,其分类流程如下:
-
将一张图片分成若干patches。每一个patch的长宽必须可以被原图的长宽整除。使用公式表示维度的变化如下:
[ b , c , l , w ] − > [ b , c , ( n 1 ∗ l p a t c h ) , ( n 2 ∗ w p a t c h ) ] − > [ b , c , n 1 ∗ n 2 , l p a t c h , w p a t c h ] [b,c,l,w]->[b,c,(n_1*l_{patch}),(n_2*w_{patch})]->[b,c,n_1*n_2,l_{patch},w_{patch}] [b,c,l,w]−>[b,c,(n1∗lpatch),(n2∗wpatch)]−>[b,c,n1∗n2,lpatch,wpatch]
最后,每一个batch中会有 n 1 ∗ n 2 n_1 * n_2 n1∗n2 个patch,每一个patch的维度是 [ l p a t c h , w p a t c h ] [l_{patch},w_{patch}] [lpatch,wpatch], c c c为图像的通道数。
-
将每一个patch以某种形式映射到一维,可以是简单的展开,也可以展开后使用线性层映射。
此步骤对应图片中左图粉色框。此处假设我们将图片简单展开之后,又经过了一个线性层映射,并最终使其维度变为 d i m dim dim,是用公式表示其维度变化如下:
$ [b,c,n_1n_2,l_{patch},w_{patch}]->[b,n_1n_2,c,l_{patch},w_{patch}]->[b,n_1n_2,cl_{patch}w{patch}]-经过一个线性层->[b,n_1n_2,dim]$
-
此时一个batch中的维度为 [ n 1 ∗ n 2 , d i m ] [n_1*n_2,dim] [n1∗n2,dim],向每一个batch的最前面都加入一个cls_token向量,维度为 [ 1 , d i m ] [1,dim] [1,dim],使得每一个batch的维度变为 [ n 1 ∗ n 2 + 1 , d i m ] [n_1*n_2+1,dim] [n1∗n2+1,dim]。之后随机初始化大小为 [ n 1 ∗ n 2 + 1 , d i m ] [n_1*n_2+1,dim] [n1∗n2+1,dim]的可训练的随机矩阵pos_embedding。与每一个batch相加,作为每一个batch的位置编码。到此,完成了左图中的 Patch +Position Embedding。
-
**经过上述处理,开始的输入被转换成维度为 [ b , n 1 ∗ n 2 + 1 , d i m ] [b,n_1*n_2+1,dim] [b,n1∗n2+1,dim]的输入,**之后将其传入Transformer Encoder中,根据多头注意力机制将输入中的特征提取进入步骤3中手动添加的cls_token中,并输出cls_token。Transformer Encoder在后面详细介绍
-
将cls_token送入MLP(多层感知机)进行分类。多层感知机是一个简单的带有激活函数的全连接神经网络。
图中需要注意的部分
左图
- 每一个patch不一定要被简单的拉伸为一维,也可以通过一个线性层映射到合适的维度
- Patch+Position Embedding 部分,进行的是两个操作,分别是加上cls_token和加上位置信息。
- cls_token以及位置编码都是可以训练的参数
- 不要被紫色的数字信息所在位置迷惑,只有添加cls_token会改变输入向量的维度,添加位置信息不会改变维度,位置信息与输入信息只是简单相加,在后面代码中还会提示,那时会看的更清楚。
- 灰色部分 Transformer Encoder 并非一层结构,可能是由多层Transformer Encoder Layer组成的,右图中左上角有 “L*” 指明了这一点。
右图
- 注意多头的处理是将输入拆开,而不是将输入重复到头数的维度。简单来说就是每一个头只能看到输入的部分信息,而不是全部信息,这点在后面的讲解中会重点介绍。
代码实现
实现过程中涉及到transformer Encoder与Attention的部分会先进行模型原理说明。
下面按照程序的流程拆解整体的代码
图片patch化
代码逻辑
首先获取训练集图片的大小,并指定每一个patch的大小,由此计算出一个大图片何以被切割成多少个小patch。之后调用
from einops.layers.torch import Rearrange
提供的Rearrange函数,将每一个patch变成一维。
代码实现
'''
pair()函数的作用是将数字扩增为元组,如果传入的image_size是(size,size)类型的,函数将不会处理;
若之传入一个数字size,pair()函数会将其扩增为(pair,pair)的格式并传给前面的变量
'''
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
# 此处是验证patch的边长可以被图片的对应边长除尽,否则不能将图片patch化
assert image_height % patch_height ==0 and image_width % patch_width == 0
# 一个图片可以被分成num_patches个patch
num_patches = (image_height // patch_height) * (image_width // patch_width)
# 对于一个patch,被展开成一维之前维度是[c,patch_height,patch_width],展开后是[channels*patch_height*patch_width]
patch_dim = channels * patch_height * patch_width
# 此处的池化与卷积的池化有区别,此处是指最后获取的分类信息是只获取保存在cls_token中的,还是将所有输出平均处理后再用于分类
assert pool in {'cls', 'mean'}
'''
这里是维度变化的重要部分,可以观察到将每一个patch展平的操作,并且在展平后,还通过一个线性层映射到了dim维度
'''
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width),
nn.Linear(patch_dim, dim)
)
Patch+Position Embedding
代码逻辑
这部分代码逻辑很简单,每一个batch中图片已经被变成 [ n u m _ p a t c h e s , d i m ] [num\_patches,dim] [num_patches,dim]维度的矩阵,在矩阵第一行之上拼接一个 [ 1 , d i m ] [1,dim] [1,dim]维的cls_token,将一个batch的维度变为 [ n u m _ p a t c h e s + 1 , d i m ] [num\_patches + 1,dim] [num_patches+1,dim]的矩阵,然后再加上一个 [ n u _ p a t c h e s + 1 , d i m ] [nu\_patches + 1,dim] [nu_patches+1,dim]维度的位置编码信息(此位置编码开始被随机化处理,但是可以训练),对每一个patch如是操作,完成此部分代码。
代码实现
参数定义部分
'''
dim:经过线性层后patch的维度
由于cls_token需要拼接在输入上面,所以会改变输入的维度,所以pos_embedding第二维为num_patches + 1
注意,此时cls_token的维度是(1,1,dim),在embedding部分会扩增为(b,1,dim),做到对每一个batch都操作
'''
self.cls_token = nn.Parameter(torch.randn(1, 1, dim)) # nn.Parameter()定义可学习参数
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))
embedding部分
# 图片patch化
x = self.to_patch_embedding(img) # b c (h p1) (w p2) -> b (h w) (p1 p2 c) -> b (h w) dim
b, n, _ = x.shape # b表示batchSize, n表示每个块的空间分辨率, _表示一个块内有多少个值
# self.cls_token: (1, 1, dim) -> cls_tokens: (batchSize, 1, dim)
# 对应此部分代码逻辑中提到的将其扩增为(b,1,dim)
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
# 将cls_token拼接到patch token中去 (b, 65, dim),此部分改变x的维度
x = torch.cat((cls_tokens, x), dim=1)
# 加上位置编码,此部分不改变x的维度
x += self.pos_embedding[:, :(n+1)]# 加位置嵌入(直接加)(b, 65, dim)
Transformer Encoder
此部分内容比较复杂,包含了Muti-Head Attention与Transformer Encoder,我会从注意力机制过渡到多头注意力机制,这也是此部分的重点。
在ViT中的Transformer结构与自然语言处理中有不同,ViT中的Transformer Encoder的结构如左图所示,在此贴出。
输入
此部分的输入是Embedded Pathes,对应的是Patch+Position Embedding处理后的图片数据,维度为 [ b a t c h s i z e , n u m _ p a t c h e s , d i m ] [batchsize,num\_patches,dim] [batchsize,num_patches,dim]。
Norm层
代码逻辑
ViT与Transformer的Norm层在不同的位置,这层的作用是将 [ b a t c h s i z e , n u m _ p a t c h e s , d i m ] [batchsize,num\_patches,dim] [batchsize,num_patches,dim]中的最后一维所对应的数据标准化(即dim维所对应的数据),加快模型的收敛速度。所以只需要对应的LayerNorm函数处理即可。
代码实现
'''
这层除了标准化之外,还设置了可传入的参数fn,表示标准化之后的操作(当然也可以不这么设计)
按照上图的结构,fn为 Mutil-Head Attention 以及 MLP
'''
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
# 对x的最后一维(dim维)进行norm化
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
Mutil-Head Attention层
在这里,我会从注意力机制过渡到多头注意力机制。
注意力机制(为了引出多头注意力机制)
代码逻辑
由于神经网络的容量有限,并且在模型中我们还使用了cls_token来保存图片中的信息。为了避免图片中信息过多,稀释或者覆盖了重要的信息,我们希望有一种方式,使得模型更加关注图像中的重要部分,而降低不重要部分的比重(并非完全不管之,只是降低其权重)。
Attention机制在自然语言处理的机器翻译中被广泛使用,也可以在图像处理中发挥作用,但是并没有在机器翻译应用场景下显的直观(由于patch之间的关联性并没有单词之间的关联性显得直观)。
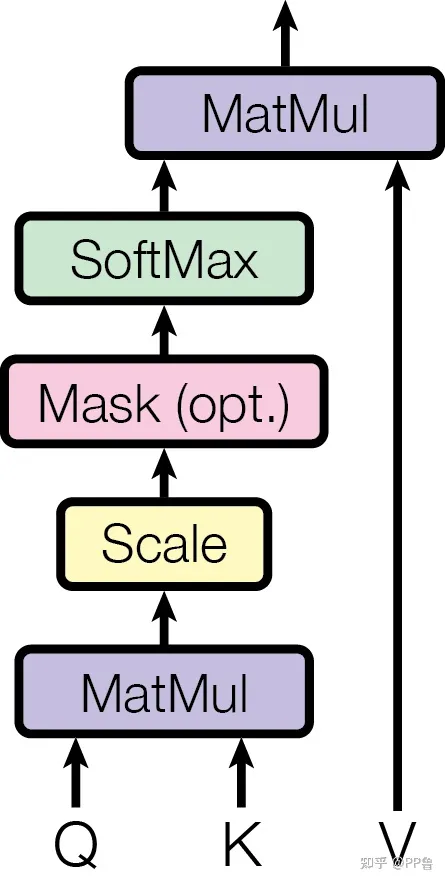
下图画出了attention中的基本结构:
 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q9GHPpZ9-1667396655969)(attention1.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q9GHPpZ9-1667396655969)(attention1.png)]
这里绿色向量是单词经过embedding之后的表示,在本模型中,应该对应每一个patch被embedding后的形状。即 X 1 X_1 X1 与 X 2 X_2 X2 是两个patch经过embedding之后的结果。
自注意力机制本质是计算各个向量之间的相关度,模型不使用直接的输入来计算相关度,而是使用 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV 三个矩阵先对输入做映射,生成 q i , k i , v i q_i,k_i,v_i qi,ki,vi 三个向量,再通过三个向量计算相似度。
q向量又叫Query向量,k向量又叫Key向量。我们将 q i q_i qi与 k j k_j kj向量相乘,再进行归一化,得到的数字代表 X i X_i Xi与 X j X_j Xj的相关性。这里有一个很容易迷惑的部分就是,为什么计算相似度的时候不直接使用 q i q_i qi与 q j q_j qj相乘,再归一化,而是要引入向量k在其中横插一脚?这个问题困扰我很久,经过不断的查找,结论如下:
**在自注意力机制中, W Q W_Q WQ 与 W K W_K WK 没有区别!!!**但是在其他的注意力模型中,可能 W K W_K WK 是以硬编码形式写好的,并非训练得到,所以为了保持模型的一致性,此处依旧引入了 W K W_K WK;关于 W V W^V WV矩阵以及V向量(value,代表一个patch的value),是为了让模型考虑全局信息,在下面会说到。
下面通过Attention机制的计算流程,讲解Attention的计算逻辑。
首先随机初始化 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV 三个矩阵(都是可训练的网络参数),并计算得出每个patch对应的q、k、v三个向量。
将 q i 与 k j q_i与k_j qi与kj 相乘,并经过归一化与softmax层,计算得出 p a t c h i 与 p a t c h j patch_i与patch_j patchi与patchj的相似度**(i与j可以相同)**。将相似度当作对应V向量的权重,将所有V向量与权重对应相乘的结果相加,获得 Z i Z_i Zi向量。 Z i Z_i Zi向量与最大权重对应的V向量最相似。
至此,自注意力机制做到了注重局部重点信息并且考虑全局。
数学表达
Q = X ∗ W Q K = X ∗ W K V = X ∗ W V Z = S o f t m a x ( Q K T d K ) V 其中 d K 是输入向量隐藏层的维度,除以 d k 目的是为了将输入的 x 归一化,防止 s o f t m a x 值过大,导致反向传播时偏导数为 0 。 Q=X*W^Q \\ K=X*W^K \\ V=X*W^V \\ Z=Softmax(\frac{QK^T}{\sqrt{d_K}})V \\ 其中d_K是输入向量隐藏层的维度,除以\sqrt{d_k}目的是为了将输入的x归一化,防止softmax值过大,导致反向传播时偏导数为0。 Q=X∗WQK=X∗WKV=X∗WVZ=Softmax(dKQKT)V其中dK是输入向量隐藏层的维度,除以dk目的是为了将输入的x归一化,防止softmax值过大,导致反向传播时偏导数为0。
多头注意力机制(模型中实际使用到的)
代码逻辑

为了解决自注意力机制中过度关注自身的问题,引入了多头注意力机制。即初始化多个Q,K,V权重矩阵,并且将输入X(Patch+Position Embedding的结果)拆开,目的是为了能从多个角度获取到patch中的信息。具体的拆解流程在代码中详述。
在看这部分时,我的困惑在于为什么加上了多个头,就要将X拆开?将X复制多份也应该可以满足多头分别处理的效果。经过查证和思考,我觉得有以下原因:
- 如果简单的将X复制多份,可能会导致训练出的Q、K、V过于相似,达不到分别关注不同信息的目的;反而将输入拆开,可以迫使不同的Q、K、V见到不同的输入,所以也会训练出不同的Q、K、V。
- 将输入拆开而不是将其复制多份,可以不增加网络的计算量。
之后对于每一个头计算独立的Attention(如果是8个头,每个头计算1/8的子空间的Attention,之后再将其拼接),拼接后经过一个线性映射后输出,完成Multi-Head Attention的计算。
结合上面对多头注意力流程的描述,我们来看一下多头注意力计算过程中输入维度的变化。
KaTeX parse error: Invalid size: 'b,patch\_dim,heads\_num,(dim/heads\_num)' at position 35: …\ (输入X的维度)->\\ [̲b̲,̲p̲a̲t̲c̲h̲\̲_̲d̲i̲m̲,̲h̲e̲a̲d̲s̲\̲_̲n̲u̲m̲,̲(̲d̲i̲m̲/̲h̲e̲a̲d̲s̲\̲_̲n̲u̲m̲)̲]̲\ (将多头考虑其中)-为了计…
如果输入的dim为512维,且有8个head,则每一个head计算并生成64维的Attention向量,将8个64维的Attention向量拼接,得到最终的512维的Mutil-head Attention。
代码实现
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
'''
默认有8个头,每个头处理64维的信息,则用于计算注意力的维度应为512维
注意,此维度和输入维度不同,我的代码中输入dim为256,在这里会通过一个线性层映射为512维的输入
'''
super().__init__()
# 用于计算注意力的维度
inner_dim = dim_head * heads
project_out = not (heads == 1 and dim_head == dim)
self.heads = heads
# 用于归一化的变量,图中的dk
self.scale = dim_head ** -0.5
# 用于将输入的最后一维归一化,所以dim=-1
self.attend = nn.Softmax(dim=-1)
# 红色注释中提到的将dim映射为计算注意力维度的线性层,同时也是所谓的W^Q,W^K,W^V矩阵,需要被训练
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
# 将inner_dim的输出再次映射回dim维度的线性层,由于注意力计算不止一层,所以要保证输入和输出的维度相同,这样才能做到上一层的输出作为下一层的输入
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout),
) if project_out else nn.Identity()
def forward(self, x):
b, n, _, h = *x.shape, self.heads
# 这里的qkv是输入与W矩阵相乘之后的结果,也就是上文中提到的qkv向量
# chunk(3,dim=-1)目的是将qkv向量从最后一维拆成三分,分别分给q、k、v,此时qkv是由三个Tensor的tuple
qkv = self.to_qkv(x).chunk(3, dim=-1)# (b, n(65), dim*3) ---> 3 * (b, n, dim)
# 通过map函数将q、k、v的维度由[b,patch_num,inner_dim]变为[b,heads_num.patch_num,(inner_dim/heads_num)]
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)# q, k, v (b, h, n, dim_head(64))
# 以下三行时每一个头计算对应Attention矩阵,可以与上述流程图或者数学公式进行对照
dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale
attn = self.attend(dots)
out = einsum('b h i j, b h j d -> b h i d', attn, v)
# 这一步是将每一个头输出的Attention向量拼接起来,将多头输出变成一个输出,可以看到将h隐藏了起来
out = rearrange(out, 'b h n d -> b n (h d)')
return self.to_out(out)
MLP层
前面说了这么多,可能已将将MLP层忘记了,幸好MLP层比较简单,很好解释。这时应该回头看看MLP所在的位置,便于我们进行后面的介绍。
代码逻辑
MLP层作用在Transformer Encoder的最后,是一个简单的线性层,但是并不一定是全连接,可以用dropout函数控制其连接的强度,避免过拟合。
增加一个MLP层可以增加模型非线性的程度(虽然模型已经很非线性了),增加预测准确度。
代码实现
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout)
)
def forward(self, x):
return self.net(x)
经过了上面这么多的介绍,我们已经对transformer的结构和实现有了基本的认识,接下来我们可以利用上面的这些class拼出来一个transformer,因为我们进行了大量的封装,所以这个transformer的代码看起来很简洁。
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
'''
dim:输入的最后一维
depth:transformer中多头注意力层(Attention层)的层数
heads:多头注意力头数
dim_head:多头注意力层的输入(与dim区别)
mlp_dim:mlp层隐藏层的维度
droupout:失活神经元的比例
'''
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
# 将Atten层与MLP层拼接起来
self.layers.append(nn.ModuleList([
PreNorm(dim, Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout)),
PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout))
]))
def forward(self, x):
# 经过多个Attention层计算
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return x
ViT整体架构(基于上述结构)
终于到了这里了,接下来我们的任务就是根据ViT的结构,结合上面不同的结构,拼出一个ViT层就好了。我们距离本篇的第一张图已经过了太久(也有可能是我写的慢的原因),我们再把ViT的结构拿到这里来对照一下。
我们在之前已经实现了很多的代码,这就意味着我们现在不用过多的讲解下面的代码。
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=1, dim_head=64, dropout=0., emb_dropout=0.):
'''
image_size:输入的图片边长
patch_size_:patch边长
num_classes:图片的分类数
dim:经过第一个线性层(粉红色)后的维度
depth:Transformer中Attention层数
heads:多头注意力机制头数
mlp_dim:ViT结构图中MLP隐藏层的维度
pool:池化方式(区别cnn中的池化)
channels:输入图片的通道数
dim_head:每个头处理的维度
'''
# 图片patch化
super().__init__()
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
assert image_height % patch_height ==0 and image_width % patch_width == 0
num_patches = (image_height // patch_height) * (image_width // patch_width)
patch_dim = channels * patch_height * patch_width
assert pool in {'cls', 'mean'}
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width),
nn.Linear(patch_dim, dim)
)
# 初始化cls_token
# nn.Parameter()定义可学习参数
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
# 初始化位置信息
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))
self.dropout = nn.Dropout(emb_dropout)
# 初始化transformer
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)
self.pool = pool
self.to_latent = nn.Identity()
# ViT模型最后的MLP层
self.mlp_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, num_classes)
)
def forward(self, img):
# 图片patch化
# [b,c,(h*p1),(w*p2)] -> [b,(h*w),(p1*p2*c)] -> [b,(h*w),dim]
x = self.to_patch_embedding(img)
# b表示batchSize, n表示h*w
b, n, _ = x.shape
# self.cls_token: (1, 1, dim) -> cls_tokens: (batchSize, 1, dim)
# 将cls_token扩增为batch个
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
# 将cls_token拼接到patch token中去,会将x的第二维增加一维(b, 64+1, dim)
x = torch.cat((cls_tokens, x), dim=1)
# print(self.pos_embedding[:,:(n+1)].shape)
# 加位置嵌入(直接加)(b, 65, dim)
x += self.pos_embedding[:, :(n+1)]
x = self.dropout(x)
x = self.transformer(x)# (b, 65, dim)
'''
获取经过transformer的x,并且提取第二维的第一个输出。之前提到这个位置是cls_token,也就是模型中用于保存图片信息并用
于分类的向量
'''
x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]
x = self.to_latent(x)
return self.mlp_head(x)
模型分类效果
MNist
ViT模型在MNist数据集上分类效果很好,经过250轮训练,在训练集上达到100%的准确率,在测试集上达到98.9%的准确率。
训练参数
| 输入维度 | 注意力头数 | transformer深度 | mlp层维度 | drop out |
|---|---|---|---|---|
| 256 | 8 | 6 | 512 | 0.1 |
| 损失函数 | 优化器 | 学习率 | 训练轮数(EPOCH) | batch size |
|---|---|---|---|---|
| CrossEntropyLoss | Adam | 1e-4(150轮之后减小为1e-5) | 250 | 32 |
分类效果
测试集上的分类效果
测试集上各类的分类效果
cifar-10
训练参数
| 输入维度 | 注意力头数 | transformer深度 | mlp层维度 | drop out |
|---|---|---|---|---|
| 512 | 8 | 8 | 1024 | 0.1 |
| 损失函数 | 优化器 | 学习率 | 训练轮数(EPOCH) | batch size |
|---|---|---|---|---|
| CrossEntropyLoss | Adam | 1e-4(0-99) 1e-5(100-199) 1e-6(200-299) | 300 | 32 |
分类效果
在训练集上达到了100%的分类效果。
测试集上分类效果
测试集上各类的分类效果
可以看到在测试集上的分类效果比测试集上差距很大,考虑是否出现过拟合。
训练时loss变化