卷积神经网络 - LeNet
文章目录
- 卷积神经网络(LeNet)
-
- 1 - LeNet
- 2 - 模型训练
- 3 - 小结
卷积神经网络(LeNet)
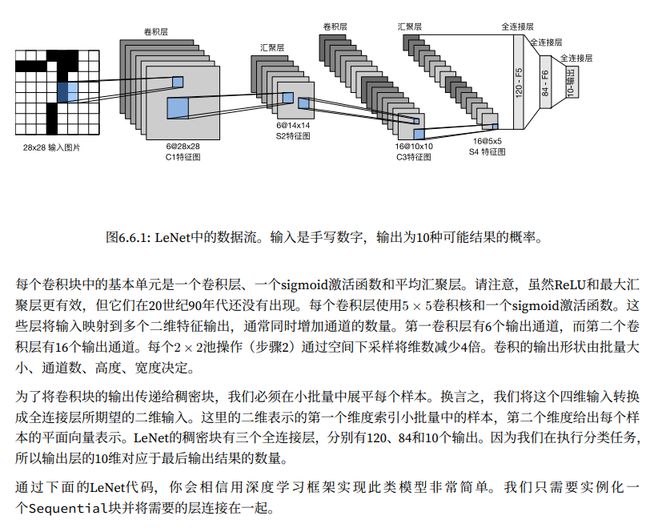
在本节中,我们将介绍LeNet,它是最早发布的卷积神经网络之一,因其在计算机视觉任务中的高效性能而收到广泛关注。这个模型是AT&贝尔实验室的研究院Yann LeCun在1989年提出的(并以其命名),⽬的是识别图像 [LeCun et al., 1998]中的⼿写数字。当时,Yann LeCun发表了第⼀篇通过反向传播成功训练卷积神经⽹络的研究,这项⼯作代表了⼗多年来神经⽹络研究开发的成果
当时,LeNet取得了与⽀持向量机(support vector machines)性能相媲美的成果,成为监督学习的主流⽅法。LeNet被⼴泛⽤于⾃动取款机(ATM)机中,帮助识别处理⽀票的数字。时⾄今⽇,⼀些⾃动取款机仍在运⾏Yann LeCun和他的同事Leon Bottou在上世纪90年代写的代码呢!
1 - LeNet
总体来看,LeNet(LeNet-5)由两个部分组成:
- 卷积编码器:由两个卷积层组成
- 全连接层密集块:由三个全连接层组成
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
nn.Conv2d(1,6,kernel_size=5,padding=2),nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Conv2d(6,16,kernel_size=5),nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5,120),nn.Sigmoid(),
nn.Linear(120,84),nn.Sigmoid(),
nn.Linear(84,10))
我们对原始模型做了一点小改动,去掉了最后一层的高斯激活。除此之外,这个网络与最初的LetNet-5一致
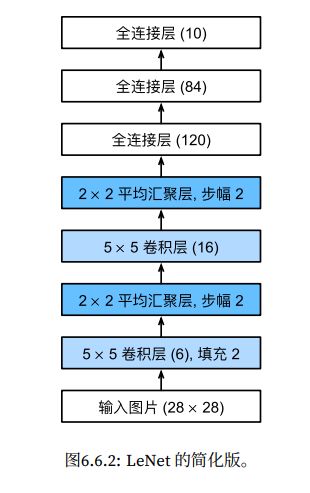
下面,我们将一个大小为28 * 28的单通道(黑白)图像通过LeNet。通过在每一次打印输出的形状,我们可以检查模型,以确保其操作与我们期望的图6.6.2一致
X = torch.rand(size=(1,1,28,28),dtype=torch.float32)
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape: \t',X.shape)
Conv2d output shape: torch.Size([1, 6, 28, 28])
Sigmoid output shape: torch.Size([1, 6, 28, 28])
AvgPool2d output shape: torch.Size([1, 6, 14, 14])
Conv2d output shape: torch.Size([1, 16, 10, 10])
Sigmoid output shape: torch.Size([1, 16, 10, 10])
AvgPool2d output shape: torch.Size([1, 16, 5, 5])
Flatten output shape: torch.Size([1, 400])
Linear output shape: torch.Size([1, 120])
Sigmoid output shape: torch.Size([1, 120])
Linear output shape: torch.Size([1, 84])
Sigmoid output shape: torch.Size([1, 84])
Linear output shape: torch.Size([1, 10])
请注意,在整个卷积块中,与上一层相比,每一层特征的高度和宽度都减小了。第一个卷积使用2个像素的填充,来补偿5 * 5卷积核导致的特征减少。相反,第二个卷积层没有填充,因此高度核宽度都减少了4个像素。随着层叠的上升,通道的数量从输入时的1个,增加到第一个卷积层之后的6个,再到第二个卷积层之后的16个。同时,每个汇聚层的高度和宽度都减半。最后,每个全连接层减少维数,最终输出一个维数与结果分类数相匹配的输出
2 - 模型训练
现在我们已经实现了LeNet,让我们看看LeNet在Fasion-MNIST数据集上的表现
batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
虽然卷积神经网络的参数较少,但与深度的多层感知机相比,它们的计算成本仍然很高,因为每个参数都参与更多的乘法,若你有机会使用GPU,可以用它加快训练
为了进行评估,我们需要对以前描述的evaluate_accuracy函数进行轻微的修改。由于完整的数据集位于内存中,因此在模型使用GPU计算数据集之前,我们需要将其复制到显存中
def evaluate_accuacy_gpu(net,data_iter,device=None):
"""使用GPU计算模型在数据集上的精度"""
if isinstance(net,nn.Module):
net.eval() # 设置为评估模式
if not device:
device = next(iter(net.parameters())).device
# 正确预测的数量,总预测的数量
metric = d2l.Accumulator(2)
with torch.no_grad():
for X,y in data_iter:
if isinstance(X,list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(d2l.accuracy(net(X),y),y.numel())
return metric[0] / metric[1]
为了使⽤GPU,我们还需要⼀点⼩改动。与 3.6节中定义的train_epoch_ch3不同,在进⾏正向和反向传播之前,我们需要将每⼀⼩批量数据移动到我们指定的设备(例如GPU)上
如下所⽰,训练函数train_ch6也类似于 3.6节中定义的train_ch3。由于我们将实现多层神经⽹络,因此我们将主要使⽤⾼级API。以下训练函数假定从⾼级API创建的模型作为输⼊,并进⾏相应的优化。我们使⽤在 4.8.2节中介绍的Xavier随机初始化模型参数。与全连接层⼀样,我们使⽤交叉熵损失函数和⼩批量随机梯度下降
def train_ch6(net,train_iter,test_iter,num_epochs,lr,device):
"""用GOU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on',device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(),lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch',xlim=[1,num_epochs],legend=['train loss','train acc','test acc'])
timer,num_batches = d2l.Timer(),len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = d2l.Accumulator(3)
net.train()
for i,(X,y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X,y = X.to(device),y.to(device)
y_hat = net(X)
l = loss(y_hat,y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0],d2l.accuracy(y_hat,y),X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,(train_l,train_acc,None))
test_acc = evaluate_accuacy_gpu(net,test_iter)
animator.add(epoch + 1,(None,None,test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, 'f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec 'f'on {str(device)}')
现在,我们训练和评估LeNet-5模型
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
loss 0.472, train acc 0.823, test acc 0.770
65229.9 examples/sec on cuda:0
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aGO8XkNa-1663410443533)(output_13_1.svg)]
3 - 小结
- 卷积神经网络(CNN)是一类使用卷积层的网络
- 在卷积神经网络中,我们组合使用卷积层、非线性激活函数和汇聚层
- 为了构造高性能的卷积神经网络,我们通常对卷积层进行排列,逐渐降低其表示的空间分别率,同时增加通道数
- 在传统的卷积神经网络中,卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理
- LeNet是最早发布的卷积神经网络之一