梯度下降法实现求解一元线性回归问题

梯度下降法求解一元线性回归问题

课程回顾

下面就使用均方差损失函数来编写程序。

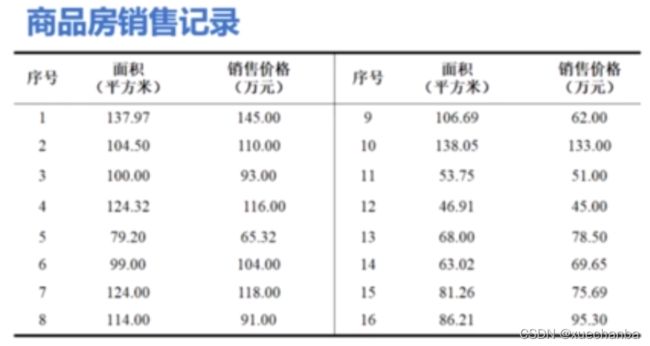
问题描述

依然是房价预测的问题，这是一个一元线性回归问题。

梯度下降法求解

求解过程可以分为五步。

步骤一

加载样本数据 x 和 y

步骤二

设置超参数 学习率 和 迭代次数

步骤三

设置模型参数初值 w₀，b₀

步骤四

训练模型，使用迭代公式更新模型参数 w ，b

步骤五

结果可视化

程序流程图

下图为程序流程图：

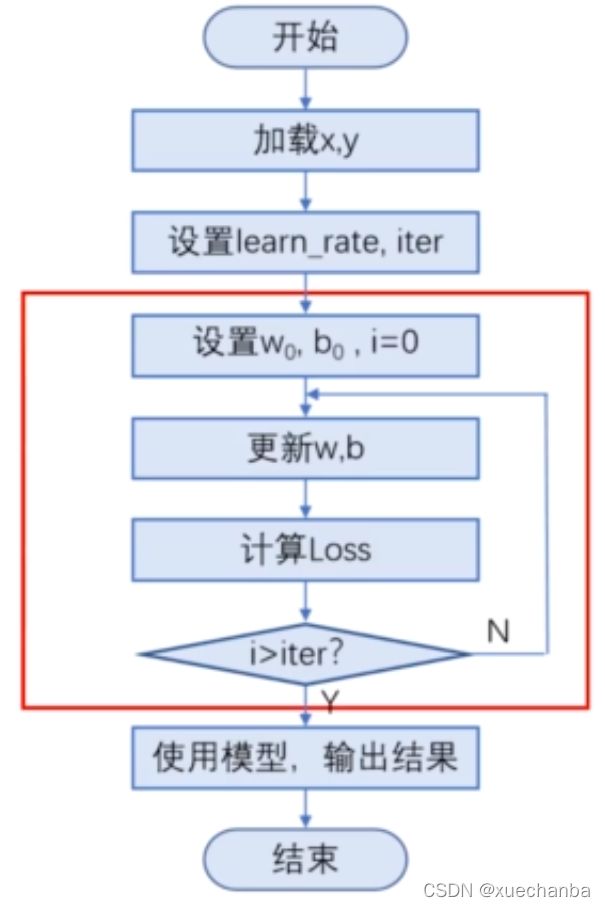
因为有迭代运算，所以需要通过循环来实现，红框中的内容即为梯度下降法的实现。首先，设置 w 和 b 的初值，设置循环变量 i ，然后利用迭代公式不断更新 w 和 b，并且计算每一次迭代的损失值，直到循环结束为止。

在上节课中，我们知道超参数的设置非常重要，对训练结果有很大的影响，在训练之前，我们往往并不知道这个超参数应该设置为多少，一般需要根据经验反复尝试，同时观察算法是否收敛，并且达到了我们需要的精度。

编程实现

import numpy as np
import matplotlib.pyplot as plt

# 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']

# 第一步：加载数据
# x 是商品房面积
x = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
              106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])  # (16, )

# y 是对应的实际房价
y = np.array([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00, 91.00,
              62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30])  # # (16, )

# 第二步：设置超参数
learn_rate = 0.00001
itar = 100  # 迭代次数, 这里让它迭代 100 次

# 如果每次迭代次数都输出结果, 输出就会很长, 这里让它每迭代 10 次就输出一次结果
display_step = 10  # 它不属于超参数, 因为它的取值并不会影响模型的训练。

# 第三步：设置模型参数初值
# 在Numpy的random模块中，使用seed()函数设置随机种子,
# 例如这里就是设置随机种子为612，然后生成随机数。
np.random.seed(612)
# 产生标准正态分布(标准差是1均值是0)的数组, 这里参数为空, 所以返回的是一个浮点数字
w = np.random.randn()
b = np.random.randn()

# 第四步：训练模型
mse = []  # 这是个Python列表, 用来保存每次迭代后的损失值

# 下面使用 for 循环来实现迭代
# 循环变量从 0 开始, 到 101 结束,循环 101 次, 为了描述方便, 以后就说迭代 100 次
# 同样, 当 i 等于 10 时, 我们就说第十次迭代
for i in range(0, itar + 1):
    # 首先计算损失函数对 w 和 b 的偏导数
    dL_dw = np.mean(x*(w*x+b-y))
    dL_db = np.mean(w*x+b-y)

    # 然后使用迭代公式更新 w 和 b
    w = w - learn_rate * dL_dw
    b = b - learn_rate * dL_db

    # 我们希望能够观察到每次迭代的结果, 判断是否收敛或者什么时候开始收敛
    # 因此需要使用每次迭代后的 w 和 b 来计算损失, 并且把它显示出来

    # x 是一个长度为16的一维数组
    pred = w * x + b   # 使用当前这次循环得到的 w 和 b, 计算所有样本的房价的估计值
    Loss = np.mean(np.square(y-pred)) / 2  # 使用房价的估计值和实际值计算均方误差
    mse.append(Loss)  # 把得到的均方误差加入列表 mse

    if i % display_step == 0:
        print("i：%i, Loss：%f, w：%f, b：%f" % (i, mse[i], w, b))

"""
i：0, Loss：3874.243711, w：0.082565, b：-1.161967
i：10, Loss：562.072704, w：0.648552, b：-1.156446
i：20, Loss：148.244254, w：0.848612, b：-1.154462
i：30, Loss：96.539782, w：0.919327, b：-1.153728
i：40, Loss：90.079712, w：0.944323, b：-1.153435
i：50, Loss：89.272557, w：0.953157, b：-1.153299
i：60, Loss：89.171687, w：0.956280, b：-1.153217
i：70, Loss：89.159061, w：0.957383, b：-1.153156
i：80, Loss：89.157460, w：0.957773, b：-1.153101
i：90, Loss：89.157238, w：0.957910, b：-1.153048
i：100, Loss：89.157187, w：0.957959, b：-1.152997
"""

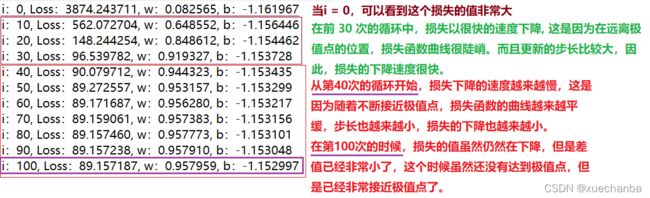
梯度下降法得到的数值解是一个近似值。在收敛之后，只要达到精度要求，就可以停止迭代，否则可以继续迭代，直到满足精度要求为止。

下面，再把模型训练的结果进行可视化。

import numpy as np
import matplotlib.pyplot as plt

# 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']

# 第一步：加载数据
# x 是商品房面积
x = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
              106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])  # (16, )

# y 是对应的实际房价
y = np.array([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00, 91.00,
              62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30])  # # (16, )

# 第二步：设置超参数
learn_rate = 0.00001
itar = 100  # 迭代次数, 这里让它迭代 100 次

# 如果每次迭代次数都输出结果, 输出就会很长, 这里让它每迭代 10 次就输出一次结果
display_step = 10  # 它不属于超参数, 因为它的取值并不会影响模型的训练。

# 第三步：设置模型参数初值
# 在Numpy的random模块中，使用seed()函数设置随机种子,
# 例如这里就是设置随机种子为612，然后生成随机数。
np.random.seed(612)
# 产生标准正态分布(标准差是1均值是0)的数组, 这里参数为空, 所以返回的是一个浮点数字
w = np.random.randn()
b = np.random.randn()

# 第四步：训练模型
mse = []  # 这是个Python列表, 用来保存每次迭代后的损失值

# 下面使用 for 循环来实现迭代
# 循环变量从 0 开始, 到 101 结束,循环 101 次, 为了描述方便, 以后就说迭代 100 次
# 同样, 当 i 等于 10 时, 我们就说第十次迭代
for i in range(0, itar + 1):
    # 首先计算损失函数对 w 和 b 的偏导数
    dL_dw = np.mean(x*(w*x+b-y))
    dL_db = np.mean(w*x+b-y)

    # 然后使用迭代公式更新 w 和 b
    w = w - learn_rate * dL_dw
    b = b - learn_rate * dL_db

    # 我们希望能够观察到每次迭代的结果, 判断是否收敛或者什么时候开始收敛
    # 因此需要使用每次迭代后的 w 和 b 来计算损失, 并且把它显示出来

    # x 是一个长度为16的一维数组
    y_pred = w * x + b   # 使用当前这次循环得到的 w 和 b, 计算所有样本的房价的估计值
    Loss = np.mean(np.square(y-y_pred)) / 2  # 使用房价的估计值和实际值计算均方误差
    mse.append(Loss)  # 把得到的均方误差加入列表 mse

    if i % display_step == 0:
        print("i：%i, Loss：%f, w：%f, b：%f" % (i, mse[i], w, b))

"""
i：0, Loss：3874.243711, w：0.082565, b：-1.161967
i：10, Loss：562.072704, w：0.648552, b：-1.156446
i：20, Loss：148.244254, w：0.848612, b：-1.154462
i：30, Loss：96.539782, w：0.919327, b：-1.153728
i：40, Loss：90.079712, w：0.944323, b：-1.153435
i：50, Loss：89.272557, w：0.953157, b：-1.153299
i：60, Loss：89.171687, w：0.956280, b：-1.153217
i：70, Loss：89.159061, w：0.957383, b：-1.153156
i：80, Loss：89.157460, w：0.957773, b：-1.153101
i：90, Loss：89.157238, w：0.957910, b：-1.153048
i：100, Loss：89.157187, w：0.957959, b：-1.152997
"""
# 创建Figure对象
plt.figure()

# 绘制散点图
# 指定x、y、z坐标，并用蓝色的‘*’标记
plt.scatter(x, y, c='red', label="销售记录")
plt.scatter(x, y_pred, c='blue', label="梯度下降法")

# 这里也可以使用plt中的设置标签的方法来进行设置
plt.xlabel('Area', color='r', fontsize=14)
plt.ylabel('Price', color='r', fontsize=14)
plt.plot(x, y_pred, color="blue")

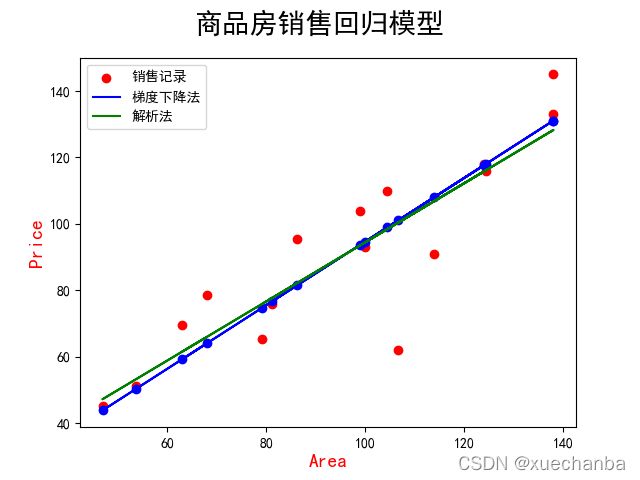
plt.suptitle("商品房销售回归模型", fontsize=20)
plt.legend(loc="upper left")

# 将创建好的图像对象显示出来
plt.show()

运行结果如下：

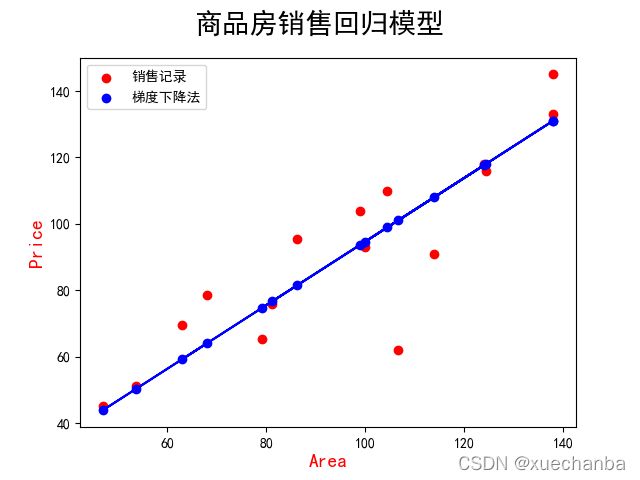
上图中，红色的点是实际的销售房价，蓝色的点是预测出的房价，蓝色的直线是训练得到的模型。那么这个模型是否准确呢？

在之前求得的解析解为：
w = 0.8945605120044221、b= 5.410840339418002
解析解是一个精确的结果，现在，我们可以把解析解对应的线性模型也绘制出来进行比较。

plt.plot(x, 0.89*x+5.41, color="green", label="解析法")

上图中绿色的直线就是解析法得到的线性模型。

可以看到采用梯度下降法得到的模型和它有一定的偏差，但是在可以接受的范围之内，如果不满足精确要求，也可以进一步增多迭代次数，继续更新权值，让 w 和 b 更接近极值点。下图展示了模型直线的变化过程。

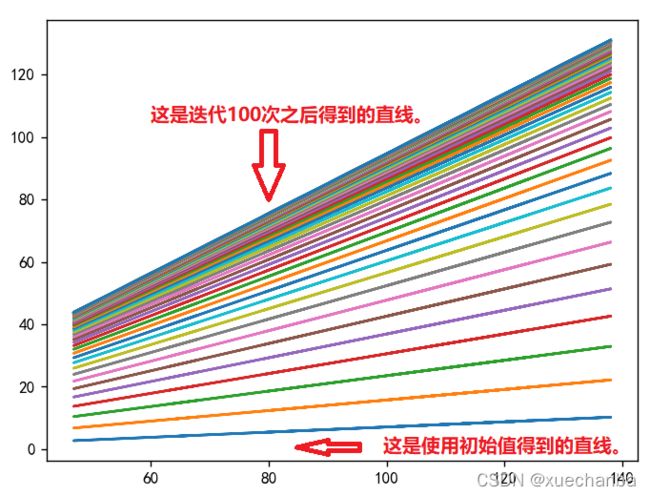
要实现这一效果，只需要在 for 循环的最后，加上这么一条语句。

for i in range(0, itar + 1):
	......
	......
	plt.plot(x, y_pred)  # 有默认的一组颜色，线条过多时，该组默认颜色用完后, 将重复使用。 
	if......
	......

除此之外，还可以通过下图更加清楚地观察到损失值的变化。

# 创建第二个Figure对象
plt.figure()

plt.plot(mse)
plt.xlabel('Iteration', color='r', fontsize=14)
plt.ylabel('Loss', color='r', fontsize=14)
plt.suptitle("损失值变化曲线图", fontsize=20)

# 将创建好的图像对象显示出来
plt.show()

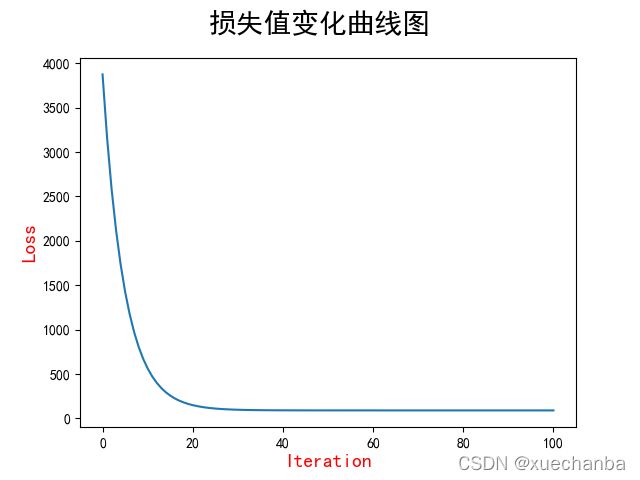
这张图中的横坐标是迭代次数，纵坐标是损失值。一开始时，损失值非常大，经过20次迭代后，损失值迅速下降，然后逐渐减缓。在 89 附近收敛。

在这张图中，因为开始时的损失值非常大，所以纵坐标的刻度也非常大，导致从第20次迭代之后，损失的下降很难直接在这张图中看出来，如果想要观察到第20次迭代之后的损失变化的情况，可以把 plot 函数的参数修改一下。
直接使用第20次迭代之后的损失数据。

plt.plot(range(20, 100), mse[20:100])

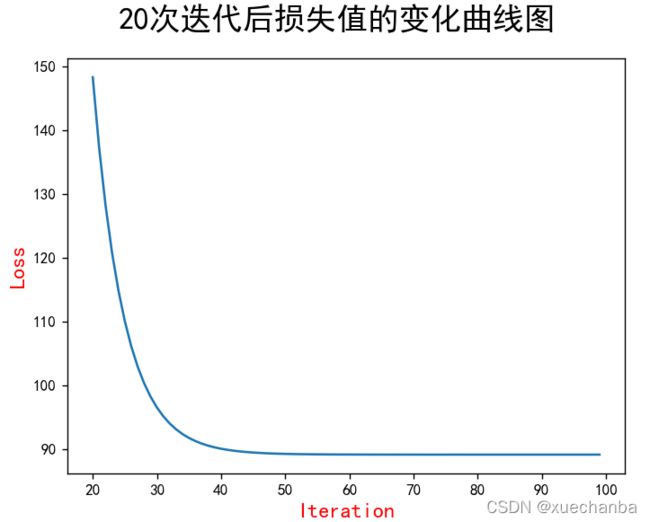
从上图中，可以看出，在第20到第40次迭代时，损失下降的也很快。40次之后就逐渐平缓了。采用同样的方法，可绘制出第40次迭代之后的损失变化的情况。

plt.plot(range(40, 100), mse[40:100])

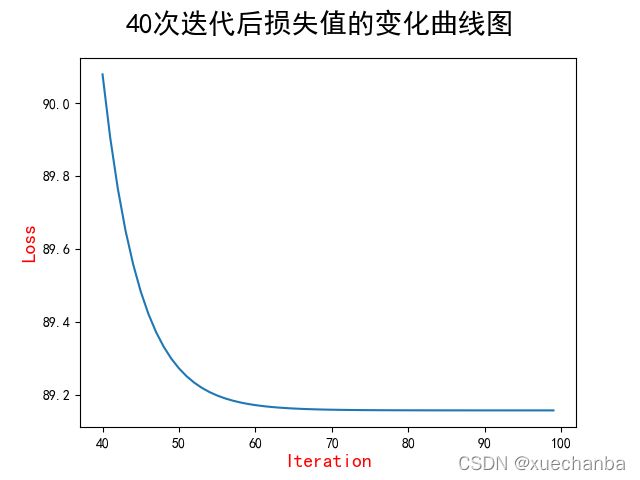
另外，需要注意的是，这个图是在训练模型的过程中损失函数的值变化的曲线，而不是损失函数的曲线图。

损失函数本身应该和下图相似：

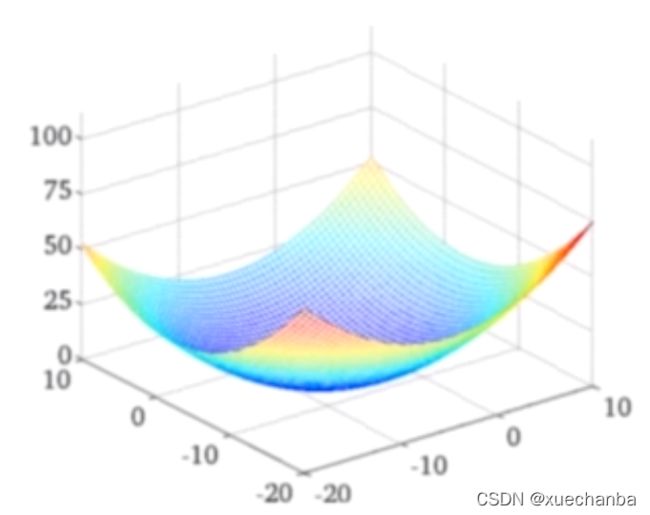
为了更好更直观的展示预测值和实际值之间的差距。可以使用下面这种图：

# 创建Figure对象
plt.figure()
plt.plot(y, color="red", marker='o', label="销售记录")
plt.plot(y_pred, color="blue", marker='o', label="梯度下降法")

plt.xlabel('Sample', color='r', fontsize=14)
plt.ylabel('Price', color='r', fontsize=14)
plt.suptitle("估计值 & 标签值", fontsize=20)

# 将创建好的图像对象显示出来
plt.show()

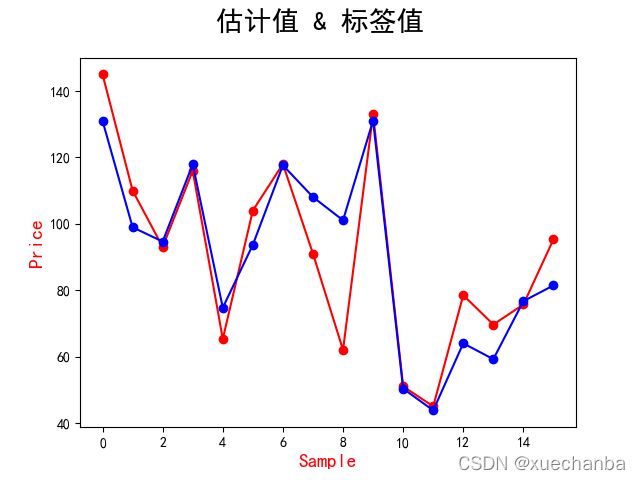
这个图中的横坐标是样本序号。一共有16个点，每个点对应一套商品房，纵坐标是房价，红色的数据点是样本数据，它的纵坐标是每套商品房的实际销售价格，蓝色的点是我们通过模型预测出来的房价，可以看到，有些房价的估计很准确，而有些偏差。

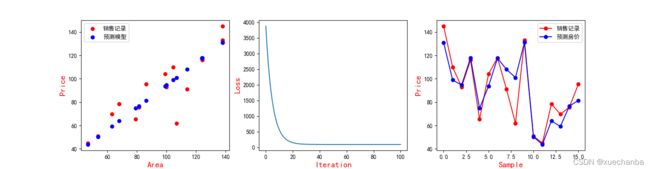
最后，为了使得结果更加便于观察，可以把这些图放在同一个画布中显示。

# 创建Figure对象
plt.figure(figsize=(16, 4))

plt.subplot(1, 3, 1)

# 绘制散点图
# 指定x、y、z坐标，并用蓝色的‘*’标记
plt.scatter(x, y, c='red', label="销售记录")
plt.scatter(x, y_pred, c='blue', label="预测模型")
# 这里也可以使用plt中的设置标签的方法来进行设置
plt.xlabel('Area', color='r', fontsize=14)
plt.ylabel('Price', color='r', fontsize=14)
plt.legend(loc="upper left")

plt.subplot(1, 3, 2)
plt.plot(mse)
plt.xlabel('Iteration', color='r', fontsize=14)
plt.ylabel('Loss', color='r', fontsize=14)

plt.subplot(1, 3, 3)
plt.plot(y, color="red", marker='o', label="销售记录")
plt.plot(y_pred, color="blue", marker='o', label="预测房价")
plt.xlabel('Sample', color='r', fontsize=14)
plt.ylabel('Price', color='r', fontsize=14)
plt.legend(loc="upper right")

# 将创建好的图像对象显示出来
plt.show()

这是运行结果：