笔记：VSLAM

整体框架

1 提取特征点 2 拿特征点进行匹配（本质上就是目标追踪问题） 3 优化误差 4 回环检测 （这其实本质上是一个场景识别任务运用的是称为BOW的 词袋模型）回环检测是为了纠正误差

1 2 大致为前段   3 大致为后端   1 2 3 统称为视觉里程计部分    前端、后端、回环检测是并行的

单目相机

场景中的物体的远近和大小称为结构。如何估计单目相机运动和结构呢？从生活经验中我们知道，如果相机往右移动，那么图像里的东西就会往左边移动——这就给我们推测运动带来了信息。另一方面，我们还知道近处的物体移动快， 远处的物体则运动缓慢。于是， 当相机移动时， 这些物体在图像上的运动， 形成了视差。通过视差，我们就能定量地判断哪些物体离得远，哪些物体离的近。然而，即使我们知道了物体远近，它们仍然只是一个相对的值。想象我们在看电影时候， 虽然能够知道电影场景中哪些物体比另一些大， 但我们无法确定电影里那些物体的 “真实尺度” ：那些大楼是真实的高楼大厦，还是放在桌上的模型？而摧毁大厦的是真实怪兽，还是穿着特摄服装的演员？直观地说，如果把相机的运动和场景大小同时放大两倍，单目所看到的像是一样的。同样的，把这个大小乘以任意倍数，我们都将看到一样的景象。这说明了单目 SLAM 估计的轨迹和地图，将与真实的轨迹、地图，相差一个因子，也就是所谓的尺度（Scale）。由于单目 SLAM 无法仅凭图像确定这个真实尺度，所以又称为尺度不确定性。

双目相机

双目相机由两个单目相机组成，但这两个相机之间的距离（称为基线（Baseline） ）是已知的。我们通过这个基线来估计每个像素的空间位置——这和人眼非常相似。如果对双目相机进行拓展，也可以搭建多目相机，不过本质上并没有什么不同。计算机上的双目相机需要大量的计算才能 （不太可靠地） 估计每一个像素点的深度， 相比于人类真是非常的笨拙。双目相机测量到的深度范围与基线相关。基线距离越大，能够测量到的就越远，所以无人车上搭载的双目通常会是个很大的家伙。双目相机的距离估计是比较左右眼的图像获得的，并不依赖其他传感设备，所以它既可以应用在室内，亦可应用于室外。双目或多目相机的缺点是配置与标定均较为复杂，其深度量程和精度受双目的基线与分辨率限制，而且视差的计算非常消耗计算资源，需要使用 GPU 和 FPGA 设备加速后，才能实时输出整张图像的距离信息。因此在现有的条件下，计算量是双目的主要问题之一。

深度相机

深度相机（又称 RGB-D 相机）是 2010 年左右开始兴起的一种相机，它最大的特点是可以通过红外结构光或 Time-of-Flight（ToF）原理，像激光传感器那样，通过主动向物体发射光并接收返回的光，测出物体离相机的距离。这部分并不像双目那样通过软件计算来解决，而是通过物理的测量手段，所以相比于双目可节省大量的计算量。目前常用的 RGB-D 相机包括Kinect/Kinect V2、Xtion live pro、Realsense 等。不过，现在多数 RGB-D 相机还存在测量范围窄、噪声大、视野小、易受日光干扰、无法测量透射材质等诸多问题，在 SLAM 方面，主要用于室内 SLAM，室外则较难应用。

刻画相机坐标到真实世界坐标的转换

是使用XYZ轴的移动和一个旋转进行描述的。其中对旋转的描述常用的有欧拉角，欧拉变换（变换矩阵）以及四元数三类，欧拉角比较直观但带有奇异性，而四元数不带有奇异性故而实际工程中更为常用。实际工程的操作步骤即是使用一种SLAM算法（如ORB-SLAM）估计沿XYZ轴三个方向的移动以及相对于初始坐标系的转动并转变为四元数共7个量，合成变换矩阵后作为相机的外参，而相机的内参是经过“标定”步骤获得的，标定的内参和通过SLAM算法获得的外参通过“灯孔模型”即可使用深度图求解对应像素在相机坐标系下的坐标，然后通过变换矩阵求解（乘）对应像素在世界坐标系下的真实坐标，将真实坐标拼合在一起即为点云。

                             

还有就是记住内参矩阵K，在之后会经常接触它：像素坐标与成像平面之间，相差了一个缩放和一个原点的平移。我
们设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍，把 α*f 合并成 f x ，把 β*f 合并成 f y，同时，原点平移了 [c x ,c y ] T。f为焦距，单位为米，α和β 单位是像素每米，所以α*f 单位为像素。

标定

标定的参数在不同情况下是不固定的，双目相机内外参都可标定，没错双目相机不经过SLAM算法仍然可以生成点云，理所当然只是不太精确而已。所谓的外参也正是SLAM的过程所要求解的东西。

李群和李代数

李群与李代数部分的内容都是关于表示旋转矩阵的内容。

知道相机坐标系中的坐标如何表示为真实世界坐标系中的位置后要明确我们的任务不仅仅是表示，还要求求解。这就会涉及优化问题，而变换矩阵是一个有约束优化问题。求解起来往往很麻烦。解决方法是群论：变换矩阵转换为李群。但仍存在常用问题是优化方法都会涉及到求导，因此可导性是个很重要的需求指标，而李群也是不可导的。这就需要通过指数映射转变为李代数。李代数是可导的。问题就可以转化为无约束非线性优化了。

李代数到李群的转化是指数映射，李群到李代数的转化是对数映射。

非线性优化

到目前为止应该掌握了两个方程：用来描述刚体运动的描述方程以及观测方程，前者是根据传感器的输入输出定位结果，后者通过观测结果进行建图。前者即是欧拉角、四元数以及李群李代数的上一级概念，后者是灯孔模型和内外参的上一级概念。

       

那么问题就转变为在求解一个状态估计的问题

 

一个状态估计问题不太容易求解（后验分布未知，就算分布已知也无法预估内参数--这是课程原话，我还没有理解），但可以将根据观测数据求状态估计转化为是在求后验概率。

 

解释一下上图的消参过程：最大化似然先验去评估参数x，分母P（z）与x无关所以消掉。P（x）机器人轨迹的先验未知故省略。（老实说我确实没有听懂）

根据贝叶斯法则相当于最大化似然和先验的乘积，但由于不清楚机器人所在位置所以自然也就没有了先验，则问题顺理成章地转化为了最大化似然估计问题，也可以这样理解：调翻转问题为“在什么样的状态下最可能产生现在观测到的数据”。而求解最大似然问题可以转换为求解最小二乘问题，原理是：    

观察负对数形式的式子，加法左侧与x无关故省略。这时求解该式最小值相当于最小化加法右侧式子。

使用负对数的解释：将“连乘”转变为“连加”避免数值下溢。

对于误差部分：

最小化非线性二乘

假设f为非线性二乘，当f比较简单时：直接对f求导即可得到极值点或者鞍点作为最小值。f比较复杂时一般都是用迭代法求解（牛顿法、G-N、L-M）其中二阶牛顿法需要计算Hessian矩阵，G-N和L-M可以避免求解Hessian矩阵。

牛顿法：将目标函数（注意目标函数是二次）展开为下式，优化时沿着反向梯度前进即可：

                                      

G-N：牛顿法直接在二次项的x附近泰勒展开，G-N在一次项处展开，注意事项一次项。这样就使用雅克比矩阵去近似Hessian矩阵求解，描述为：
          

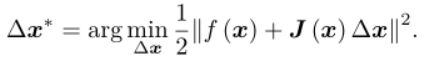
L-M：G-N虽然简单好用，但无法保证雅克比矩阵替换为H后可逆（二次近似不可靠）。L-M属于信赖区域方法，认为近似只在区域内是可靠的，信赖区间描述为：

                                                               

然后根据该信赖区间构建更鲁棒的方法。
常用库有ceres和g2o，各自的官网都有学习教程。

Ceres

上面已经提到，我们将问题转化为了最小二乘形式，这样就可以通过非线性优化程序包进行优化了。

ceres和g2o都是模板类的书写方式，找个机会写一套比较成熟的优化过程，然后保存，日后直接调用即可。

其中Ceres是直接对转化后的最小二乘优化，而g2o则需要额外的一步转化为图优化形式。

g2o

g2o全称是General Graph Optimization！所谓的通用图优化。为何叫通用呢？g2o的核里带有各种各样的求解器，而它的顶点、边的类型则多种多样。通过自定义顶点和边，事实上，只要一个优化问题能够表达成图，那么就可以用g2o去求解它。常见的，比如bundle adjustment，ICP，数据拟合，都可以用g2o来做。

ORB特征

关于ORB特征点是什么，描述子是什么，如何保证尺度不变性，如何保证旋转不变性，汉明距离是什么，如何进行特征的匹配：https://www.cnblogs.com/alexme/p/11345701.html

特征匹配

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

//函数声明C++中的必要项
void find_feature_matches(
    const Mat& img_1,  //const xxx&代表函数内外变量都不会被改变
    const Mat& img_2,
    std::vector& keypoints_1,
    std::vector& keypoints_2,
    std::vector& good_matches

);

int main ( int argc, char** argv )
{
    if(argc != 3)
    {
        cout<< " loss input"  <keypoints_1, keypoints_2;
    vectorgood_matches;
    
    //特征点检测与匹配
    find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, good_matches);
    cout<<"debug"<& keypoints_1,
                          std::vector& keypoints_2,
                          std::vector& good_matches)//定义这些变量
{
    //定义描述子变量 //还记得吗ORB由特征点和描述子两部分组成
    Mat descriptors_1, descriptors_2;
    //特征点提取器
    Ptr detector = ORB::create();
    //描述子提取器
    Ptr descriptor = ORB::create();
    //匹配器
    Ptr matcher = DescriptorMatcher::create("BruteForce-Hamming");

    //特征点检测
    detector->detect(img_1, keypoints_1);
    detector->detect(img_2, keypoints_2);

    //描述子检测
    descriptor->compute(img_1, keypoints_1, descriptors_1);
    descriptor->compute(img_2, keypoints_2, descriptors_2);

    //匹配器匹配
    vector matches;
    matcher->match(descriptors_1, descriptors_2, matches);

    //注意这里时hamming距离，计算的是二进制0和1不相同的数量
    //最大值与最小值设置相反是为了下面的循环比较
    double min_dist = 10000, max_dist = 0;

    //按照描述子数量循环
    for(int i = 0; i  max_dist) max_dist = dist;
    }

    //输出
    cout<<"Max_dist:" << max_dist <

特征匹配到位姿估计

提取出特征点后，将其两两进行匹配，然后根据匹配关系反推相机位姿。1. 当相机为单目时，我们只知道 2D 的像素坐标，因而问题是根据两组 2D 点估计运动。该问题用对极几何来解决。2. 当相机为双目、RGB-D 时，或者我们通过某种方法得到了距离信息，那问题就是根据两组 3D 点估计运动。该问题通常用 ICP 来解决。3. 如果我们有 3D 点和它们在相机的投影位置， 也能估计相机的运动。 该问题通过 PnP求解。

对极几何

对极几何依赖本质矩阵E和基本矩阵F，他们的关系如下

                                       

根据配对点的像素为止求出E或者F，然后根据E或F求出R，t。由于E与F之间只相差了相机内参，而内参在SLAM中通常是已知的，所以实践中往往使用形式简单的E，但计算上不需要焦距光心等参数进行归一化（直接使用p而不是x）所以求解F更容易。

八点法求解本质矩阵E：实际应用中可以由更多的匹配点来做这件事。

                 

此外还有一个单应矩阵H，当特征点共面或者相机发生纯旋转是，基础矩阵的自由度会下降，这就出现了所谓的退化，现实中的数据总保函一些噪声，这时候如果我们继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪声决定。为了避免退化现象造成的影响，通常我们会同时估计基础矩阵F和单应矩阵H，选择重投影误差较小的那个作为运动估计矩阵。

对极几何代码注释

void pose_estimation_2d2d (
  std::vector keypoints_1,
  std::vector keypoints_2,
  std::vector< DMatch > matches,
  Mat& R, Mat& t )
{
    // 相机内参, TUM Freiburg2
    Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );

    //-- 把匹配点转换为 vector 的形式
    vector points1;
    vector points2;

    for ( int i = 0; i < ( int ) matches.size(); i++ )
       {
        points1.push_back( keypoints_1[matches[i].queryIdx].pt );
        points2.push_back( keypoints_2[matches[i].trainIdx].pt );
       }

    //-- 计算基础矩阵F，注意这里是不需要内参的
    Mat fundamental_matrix;
    fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
    cout<<"fundamental_matrix is "< keypoints_1, keypoints_2;
    vector matches;
    //函数内局部变量修改了全局变量，输出matches
    //Mat &, reference传递，函数内部修改将会改变外部。
    find_feature_matches( img_1, img_2, keypoints_1, keypoints_2, matches );
    cout<<"一共找到了"<
    Mat t_x = (Mat_(3,3) <<
    0, -t.at(2,0), t.at(1,0),
    t.at(2,0), 0, -t.at(0,0),
    -t.at(1.0), t.at(0,0), 0);
    cout<<"t^R="< ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    // K矩阵形式（fx, 0, cx, 0, fy, cy, 0, 0, 1）
    for ( DMatch m: matches )
     {
        Point2d pt1 = pixel2cam( keypoints_1[ m.queryIdx ].pt, K );
        Mat y1 = (Mat_(3,1) << pt1.x, pt1.y, 1);
        Point2d pt2 = pixel2cam( keypoints_2[ m.trainIdx ].pt, K );
        Mat y2 = (Mat_(3,1) << pt2.x, pt2.y, 1);
        Mat d = y2.t() * t_x * R * y1;  //尺度不变性指的是t分解出来后乘以任何一个数此式仍成立
        cout << "epipolar constraint = " << d << endl;
     }
    return 0;
}

单目初始化

对 t 长度的归一化，直接导致了单目视觉的尺度不确定性（Scale Ambiguity）。例如，程序中输出的 t 第一维约 0.822。这个 0.822 究竟是指 0.822 米呢，还是 0.822 厘米呢，我们是没法确定的。因为对 t 乘以任意比例常数后，对极约束依然是成立的。换言之，在单目 SLAM 中，对轨迹和地图同时缩放任意倍数，我们得到的图像依然是一样的。
在单目视觉中，我们对两张图像的 t 归一化，相当于固定了尺度。虽然我们不知道它的实际长度为多少，但我们以这时的 t 为单位 1，计算相机运动和特征点的 3D 位置。这被称为单目 SLAM 的初始化。在初始化之后，就可以用 3D-2D 来计算相机运动了。初始化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，单目 SLAM 有一步不可避免的初始化。初始化的两张图像必须有一定程度的平移，而后的轨迹和地图都将以此步的平移为单位。
除了对 t 进行归一化之外，另一种方法是令初始化时所有的特征点平均深度为 1，也可以固定一个尺度。相比于令 t 长度为 1 的做法，把特征点深度归一化可以控制场景的规模大小，使计算在数值上更稳定些。不过这并没有理论上的差别。

初始化的纯旋转问题：

从 E 分解到 R,t 的过程中，如果相机发生的是纯旋转，导致 t 为零，那么，得到的E 也将为零，这将导致我们无从求解 R。不过，此时我们可以依靠 H 求取旋转，但仅有旋转时，我们无法用三角测量估计特征点的空间位置（这将在下文提到） ，于是，另一个结论是，单目初始化不能只有纯旋转，必须要有一定程度的平移。如果没有平移，单目将无法初始化。在实践当中，如果初始化时平移太小，会使得位姿求解与三角化结果不稳定，从而导致失败。相对的，如果把相机左右移动而不是原地旋转，就容易让单目 SLAM 初始化。因而有经验的 SLAM 研究人员，在单目 SLAM 情况下，经常选择让相机进行左右平移以顺利地进行初始化。

三角化

已知运动时求解特征点的3D位置，其实就是根据几何关系，让下式成立，然后求解s1与s2.

在单目视觉中，我们对两张图像的 t 归一化，相当于固定了尺度。虽然我们不知道它的实际长度为多少，但我们以这时的 t 为单位 1，计算相机运动和特征点的 3D 位置。这被称为单目 SLAM 的初始化。在初始化之后，就可以用 3D-2D 来计算相机运动了。初始化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，单目 SLAM 有一步不可避免的初始化。初始化的两张图像必须有一定程度的平移，而后的轨迹和地图都将以此步的平移为单位。

                                                               

PnP

PnP（Perspective-n-Point）是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时， 如何估计相机所在的位姿。前面已经说了， 2D-2D的对极几何方法需要八个或八个以上的点对（以八点法为例） ，且存在着初始化、纯旋转和尺度的问题。然而，如果两张图像中，其中一张特征点的 3D 位置已知，那么最少只需三个点对（需要至少一个额外点验证结果）就可以估计相机运动。特征点的 3D 位置可以由三角化，或者由 RGB-D 相机的深度图确定。因此，在双目或 RGB-D 的视觉里程计中，我们可以直接使用 PnP 估计相机运动。而在单目视觉里程计中，必须先进行初始化，然后才能使用 PnP。3D-2D 方法不需要使用对极约束， 又可以在很少的匹配点中获得较好的运动估计，是最重要的一种姿态估计方法。

PnP 问题有很多种求解方法：分为代数法与优化法两类。代数法例如用三对点估计位姿的 P3P， 直接线性变换 （DLT） ，EPnP（Efficient PnP），UPnP等等 。此外，还能用非线性优化的方式，构建最小二乘问题并迭代求解，也就是万金油式的 Bundle Adjustment。

在特征点提取部分基础上我们通过调用OPENCV中的EPnP来求解R与t矩阵

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;


void find_feature_matches(
    const Mat& img_1,  
    const Mat& img_2,
    std::vector& keypoints_1,
    std::vector& keypoints_2,
    std::vector& good_matches

);

//像素位置转变为相机位置函数声明
Point2d pixel2cam(const Point2d& p, const Mat& K);


int main ( int argc, char** argv )
{
    if(argc != 4)
    {
        cout<< " loss input"  <keypoints_1, keypoints_2;
    vectorgood_matches;

    find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, good_matches);
    cout<<"TotalFeaturePoints:"<(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
    //opencv下3d点群
    vectorpts_3d;
    //opencv下2d点群
    vectorpts_2d;
    //输出K矩阵检验一下
    cout<< K <(int (keypoints_1[m.queryIdx].pt.y))[int (keypoints_1[m.queryIdx].pt.x)];

        if(d ==0)
        {
            continue;
        }
        //求解深度
        float dd = d/5000.0;   
        //5000是相机参数，显然像素值0-255不够表达深度
        //像素坐标转化为相机下坐标
        Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
        //3d与2d点分别储存
        pts_3d.push_back(Point3f(p1.x*dd, p1.y*dd, dd));
        pts_2d.push_back(keypoints_2[m.trainIdx].pt);
    }
    
    //输出配对数量
    cout<<"3d-2d pairs:"<detect(img_1, keypoints_1);
    detector->detect(img_2, keypoints_2);

    
    descriptor->compute(img_1, keypoints_1, descriptors_1);
    descriptor->compute(img_2, keypoints_2, descriptors_2);

    
    vector matches;
    matcher->match(descriptors_1, descriptors_2, matches);

   
    double min_dist = 10000, max_dist = 0;

    
    for(int i = 0; i  max_dist) max_dist = dist;
    }

   
    cout<<"Max_dist:" << max_dist <(0,2)) / K.at(0,0),
        (p.y - K.at(1,2)) / K.at(1,1)
    );

}

DLT（直接线性变换）

将R和t放在一起构成一个3X4的增广矩阵，可得关系

                         

可以看出每个特征点会提供两个关于t的线性约束，由于t矩阵有12维，因此最少通过六对匹配点即可实现矩阵t的线性求解。当匹配点大于六对时可以通过SVD等方法对超定方程求解最小二乘解。

DLT的问题在于将t矩阵看做了12个未知数，忽略了之间的约束，平移向量还好办，旋转矩阵是有正交约束的，需要额外的QR分解寻找一个近似。

P3P（Perspective-3-Point）

顾名思义只需要3对点即可完成任务。我们的已知条件是ABC在世界坐标系中的位置以及abc在相机成像平面的投影坐标。

P3P本质上是利用三角形相似性质，求解投影点abc在相机坐标系下的3D坐标，最后把问题转换为一个3D到3D的位姿估计问题。后文可以看到，带有匹配信息的3D-3D位姿求解非常容易

P3P的问题在于只能利用三个点的信息，即使多于三个点也难以利用多余信息；更容易受到噪声影响，造成误匹配，算法失效。

BA（Bundle Adjustment）

百度查会告诉你是“光束法平差”，书中的意思是BA是一种概念性的东西，所以很多地方都可以用。BA属于非线性优化一类的东西所以自然也就和Ceres和g2o有关。不过查找资料来看似乎BA与g2o的联系更为紧密一些。

由于 Kinect 采集的深度图本身会有一些误差，所以 3D 点也不是准确的。我们会希望把位姿 ξ 和所有三维特征点 P 同时优化。

说白了BA就是把 PnP 问题构建成一个定义于李代数上的非线性最小二乘问题。

ICP

ICP时3d到3d的匹配过程，定义参照点集P（p1，p2, ...pn）和与之对应匹配的点集P‘（p'1，p'2, ...p'n）。显然运动关系可以表示为Pi'=R*Pi+t，则误差项表示为ei=P’i -（R*Pi+t），最小二乘形式为误差项相加。

带匹配的ICP需要质心（所有点相加）。

带匹配情况的ICP一般只有一个解，因此SVD与BA的结果相似。

激光中的ICP是不带匹配的，因此认为最近邻就是对应的匹配点。所以这时候SVD效果会不太好，这是可以考虑BA。

BA时万金油式解决方法，甚至可以定义PnP和ICP一同求解。

基于特征点的前端小结

到现在为止可以很清晰的整理出基于特征点匹配的视觉SLAM的前端流程

双目摄像头---matlab棋盘格标定---获取内参K矩阵---两幅图片提取特征点与描述子---两幅图片中的特征匹配---设定阈值删除不良匹配---获取良好匹配对像素坐标---转化为相机坐标---判断上一步中坐标为2d-2d, 3d-2d, 3d-3d中的哪一种---分别采用对极几何，PnP，ICP进行匹配----输出R， t矩阵---小结B上一步作为初值进行非线性优化（同时也是BA过程）---输出良好R， t

直接法

特征匹配法中特征点提取部分还是非常耗时的（提个ORB就要10ms）有两种

通过其他方式寻找特征点的光流法以及无配对点的纯直接法

光流法

稀疏光流（LK）稠密光流（NS）

灰度不变假设：t+dt时刻的灰度（一个三元表达式）与t时刻灰度相等，此式经泰勒展开后可得一个欠定方程

一个二元一次方程（欠定）所以不可解，则需要额外的一个假设。于是我们假设一个窗口内的光度是不变的。比如一个2x2的窗口，这样上面的式子就变为了4个方乘。

这里我们就可以看出来了，最小二乘法也可以理解为是一种解超定方程的方法

运动幅度较大时使用图像金字塔技术

光流法速度优势

只需要第一副图中提取一个角点（甚至描述都不需要提取），然后光流法追踪即可确定运行关系，故而速度很快

LK 光流跟踪法避免了描述子的计算与匹配，但本身也需要一定的计算量。在我们的计算平台上，使用 LK 光流能够节省一定的计算量，但在具体 SLAM 系统中使用光流还是匹配描述子，最好是亲自做实验测试一下。

光流法其他优势与不足

另外，LK 光流跟踪能够直接得到特征点的对应关系。这个对应关系就像是描述子的匹配，但实际上我们大多数时候只会碰到特征点跟丢的情况，而不太会遇到误匹配，这应该是光流相对于描述子的一点优势。但是，匹配描述子的方法在相机运动较大时仍能成功，而光流必须要求相机运动是微小的。从这方面来说，光流的鲁棒性比描述子差一些。

最后，我们可以通过光流跟踪的特征点，用 PnP、ICP 或对极几何来估计相机运动，这些方法在上一章中都讲过，我们不再讨论。总而言之，光流法可以加速基于特征点的视觉里程计算法，避免计算和匹配描述子的过程，但要求相机运动较慢（或采集频率较高） 。

直接法

此时最小化的不是重投影误差，而是光度误差（Photometric Error） ，也就是 P 的两个像的亮度误差。

回环检测

目的：减小或消除累积误差，得到全局一致的估计

利用回环检测可以完成（跟踪线程中的）重定位（定位初始化）

回环检测就是完成了：如何有效地检测除相机经过同一个地方这件事

词袋模型与字典

词袋，也就是 Bag-of-Words（BoW） ，目的是用“图像上有哪几种特征”来描述一个图像。例如，如果某个照片，我们说里面有一个人、一辆车；而另一张则有两个人、一只狗。根据这样的描述，可以度量这两个图像的相似性。再具体一些，我们要做以下几件事：1. 确定“人、车、狗”等概念——对应于 BoW 中的“单词” （Word） ，许多单词放在一起，组成了“字典” （Dictionary）。2. 确定一张图像中， 出现了哪些在字典中定义的概念——我们用单词出现的情况（或直方图）描述整张图像。这就把一个图像转换成了一个向量的描述。3. 比较上一步中的描述的相似程度。

字典是固定的，所以只要用 [1,1,0] T 这个向量就可以表达 A 的意义。通过字典和单词，只需一个向量就可以描述整张图像了。该向量描述的是“图像是否含有某类特征”的信息，比单纯的灰度值更加稳定。又因为描述向量说的是“是否出现” ，而不管它们“在哪
儿出现” ，所以与物体的空间位置和排列顺序无关，因此在相机发生少量运动时，只要物体仍在视野中出现，我们就仍然保证描述向量不发生变化。 基于这种特性，我们称它为Bag-of-Words 而不是什么 List-of-Words，强调的是 Words 的有无，而无关其顺序。因此，可以说字典类似于单词的一个集合。

字典由很多单词组成，而每一个单词代表了一个概念。一个单词与一个单独的特征点不同，它不是从单个图像上提取出来的，而是某一类特征的组合。所以，字典生成问题类似于一个聚类（Clustering）问题。聚类问题是无监督机器学习（Unsupervised ML）中一个特别常见的问题，用于让机器自行寻找数据中的规律的问题。BoW 的字典生成问题亦属于其中之一。首先，假设我们对大量的图像提取了特征点，比如说有 N 个。现在，我们想找一个有 k 个单词的字典，每个单词可以看作局部相邻特征点的集合，应该怎么做呢？这可以用经典的 K-means（K 均值）算法解决。

K-means 是一个非常简单有效的方法，因此在无监督学习中广为使用。简单来说，当我们有 N 个数据，想要归成 k 个类，那么用 K-means 来做，主要有以下几个步骤：
1. 随机选取 k 个中心点：c 1 ,...,c k ；
2. 对每一个样本，计算与每个中心点之间的距离，取最小的作为它的归类；
3. 重新计算每个类的中心点。
4. 如果每个中心点都变化很小，则算法收敛，退出；否则返回 1。

K-means 的做法是朴素且简单有效的， 不过也存在一些问题， 例如需要指定聚类数量、随机选取中心点使得每次聚类结果都不相同以及一些效率上的问题。总之，根据 K-means，我们可以把已经提取的大量特征点聚类成一个含有 k 个单词的字典了。现在的问题，变为如何根据图像中某个特征点，查找字典中相应的单词？仍然有朴素的思想：只要和每个单词进行比对，取最相似的那个就可以了嘛——这当然是简单有效的做法。然而，考虑到字典的通用性 x ，我们通常会使用一个较大规模的字典，以保证当前使用环境中的图像特征都曾在字典里出现过，或至少有相近的表达。如果你觉得对 10 个单词一一比较不是什么麻烦事，但对于一万个呢？十万个呢？

K叉树表达字典：它的思路很简单，类似于层次聚类，是 k-means 的直接扩展。假定我们有 N 个特征点，希望构建一个深度为 d，每次分叉为 k 的树，那么做法如下 ：
1. 在根节点，用 k-means 把所有样本聚成 k 类（实际中为保证聚类均匀性会使用k-means++） 。这样得到了第一层。
2. 对第一层的每个节点，把属于该节点的样本再聚成 k 类，得到下一层。
3. 依此类推，最后得到叶子层。叶子层即为所谓的 Words。

相似度计算

相似度计算产生评价分数（Scoring）

上面做法中， 我们对所有单词都是 “一视同仁” 的——有就是有， 没有就是没有。这样做好不好呢？考虑到， 不同的单词在区分性上的重要性并不相同。例如“的” 、 “是”这样的字可能在许许多多的句子中出现，我们无法根据它们判别句子的类型；但如果有“文档” 、 “足球”这样的单词，对判别句子的作用就更大一些，可以说它们提供了更多信息。所以概括的话，我们希望对单词的区分性或重要性加以评估，给它们不同的权值以起到更好的效果。在文本检索中，常用的一种做法称为 TF-IDF（Term Frequency–Inverse DocumentFrequency）[100, 101]，或译频率-逆文档频率 y 。TF 部分的思想是，某单词在一个图像中经常出现，它的区分度就高。另一方面，IDF 的思想是，某单词在字典中出现的频率越低，则分类图像时区分度越高。

因此我们要在词袋模型中，在建立字典时可以考虑 IDF和TF 部分。统计某个叶子节点 wi中的特征数量相对于所有特征数量的比例，作为 IDF 部分，TF 部分则是指某个特征在单个图像中出现的频率。使wi的权重等于IDF X TF。由于相似的特征可能落到同一个类中，因此实际的 v A 中会存在大量的零。无论如何，通过词袋，我们用单个向量 v A 描述了一个图像 A。这个向量 v A 是一个稀疏的向量，它的非零部分指示出图像 A 中含有哪些单词，而这些部分的值为 TF-IDF 的值。

卡尔曼滤波

属于贝叶斯估计的一类方法

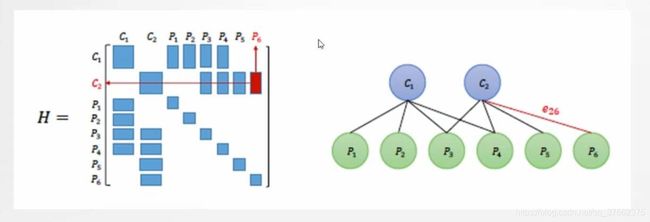
BA和图优化

图展示了BA如何向图优化中的图转换（转载于高翔SLAM十四讲）

顺便说下为什么左边的H矩阵是这个样子，因为只存在相机与路标之间的约束，不存在相机与相机，路标与路标之间的约束

求解这种方法放入过程与数值分析极其相似

概率图，图模型，gtsam，贝叶斯网等理论与应用

它与图优化是一个东西吗

当然不是，甚至有人说它是另一个阶段

多了一个可维护的动态更新部分，而不影响之前的东西

参考资料：https://zhuanlan.zhihu.com/p/53972892

先了解一下为什么

前面有一大堆的理论，我们之后再去理解。总之是需要求解一个最大后验估计问题，然后转化求解一个最小二值化问题。最小二值化问题就可以利用我们熟悉的高斯牛顿迭代法求解了

为什么我们能用迭代法求解，因为雅克比矩阵是个稀疏矩阵（有关联的路标不多，状态也是只有上一个）参考资料有叙述

迭代法求解，先进行矩阵分解（见数值分析教材）

GTSAM

其中包括isam2

必要时再学习怎么写代码

参考资料：https://www.bilibili.com/video/BV1C4411772G

G2o，GTSAM，Ceres，Tensorflow优化器的方法比较

• 首先是一些背景知识：
  • 最速梯度下降法（GD）和牛顿法可以用来优化所有种类的函数。
  • 牛顿高斯和基于牛顿高斯的LM法只能用来优化非线性最小二乘。
  • SGD是最速梯度下降法的改进，也就是每次迭代随即选取一些样本进行优化。
  • 一般大型优化问题不会用二阶的牛顿法。
• Ceres是针对所有种类的函数的优化，所以只能用最速梯度下降法。
• G2o是求解的一个标准的最小二乘
  • 
• GTSAM准确的说不是解的优化方程。而是先把一个概率图的联合概率的信息矩阵和信息向量表示出来（）。但具有物理意义的是均值和协方差。所以通过信息矩阵和协方差矩阵的换算计算出均值。这个换算里面有求逆，等于是在解方程。
• 和可以相互变换。概率图可以通过分解来简化矩阵。G2O的非线性优化中也可以通过消元来简化矩阵。所以两个方法基本是等价的。但是概率图具有一定物理意义，更容易增量扩展。
• Tensorflow用来优化神经网络，也就是线性函数嵌套一个非线性方程的函数。所以使用SGD。但是Tensorflow限定于神经网络似的函数，所以不能用Tensorflow来优化普通函数或者做SLAM

转载于：https://blog.csdn.net/ziliwangmoe/article/details/86561157，作者写得太棒了我就直接转载了。