《深度学习入门》第七章：卷积神经网络

当当当当！！！终于到正题了！！！

1. CNN（convolutional neural network, CNN）：

同样通过组装层实现，不过新出现了卷积层（convolution层）和池化层（pooling层）

2. 为什么要用卷积层（convolution）：

全连接层缺点：数据的形状被“忽视”，如：输入数据是图像时，其高、长、通道方向上的3维数据需要拉平至1维数据。而3维形状中含有重要的空间信息，如：空间上相邻的像素为相似的值、RGB的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等。
卷积层优点：可以保持形状不变。当输入数据是图像时，卷积层会以3维数据的形式接收输入数据，并同样以3维数据的形式传输至下一层。所以，CNN中可能正确理解图像等具有形状的数据。
卷积层中：有时将输入数据称为 输入特征图；输出数据称为 输出特征图。

3. 卷积运算：

相当于图像处理中的“滤波器运算”。

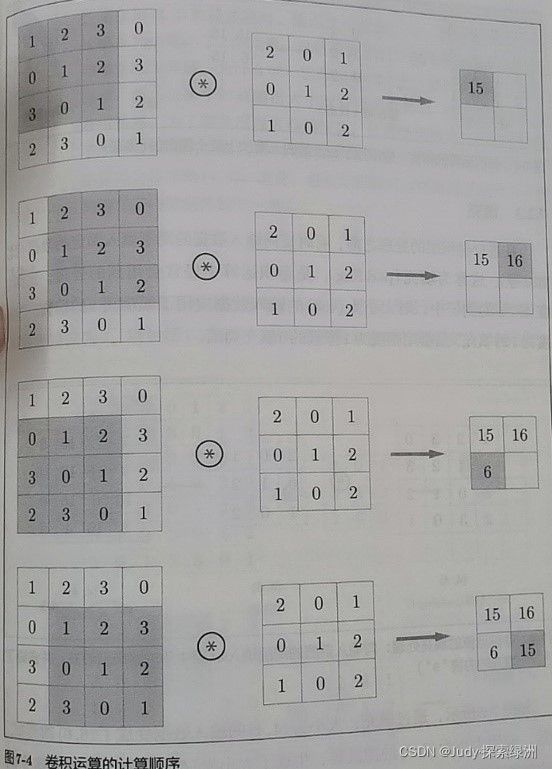
其计算过程如下，对于输入数据，卷积运算以一定间隔滑动滤波器窗口并应用，“窗口”指下图左侧灰色的3x3部分。将各个位置上滤波器的元素和输入的对应元素相乘，然后求和，最后将结果保存到输出的对应位置（该计算也称“成绩累加运算”）。

CNN中，滤波器的参数对应全连接的神经网络中的权重，偏置通常只有一个，会被加到应用了滤波器的所有的元素上。例如下图：

4. CNN中的填充

使用填充，主要是为了调整输出的大小。
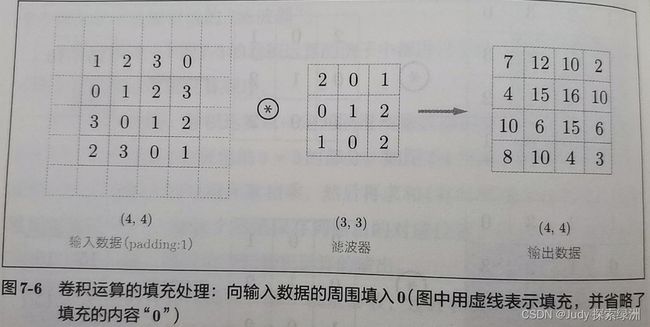
进行卷积层的处理之前，有时要想输入数据的周围填入固定的数据（如0等），称为填充。如下图左侧，对于大小为（4,4）的输入数据应用了幅度为1的填充。，即用幅度为1像素的0填充周围。填充之后。（4,4）变成了（6,6），应用（3,3）的滤波器后，生成大小为（4,4）的输出数据。（当然，填充的值可以设成任意2,3等的整数）

5. CNN中的步幅

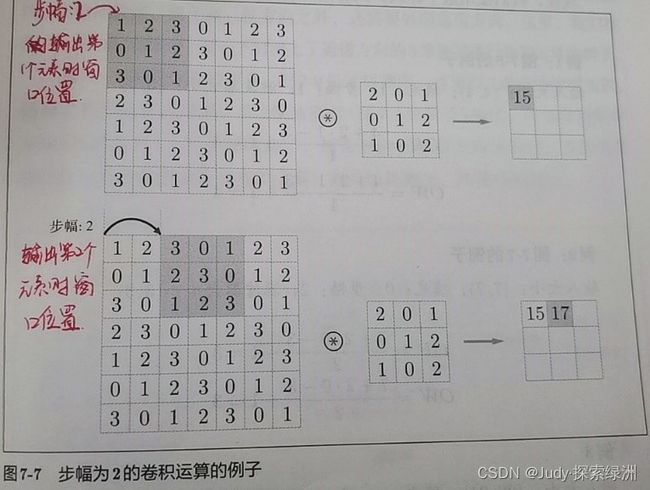
指应用滤波器的位置间隔。如下图所示：

综合3、4，增大步幅后，输出的大小会变小；而增大填充后，输出的大小会变大。将这种关系写成算式如下：
注：设定的值需要计算结果出现小数时，采用报错等对策。根据深度学习框架不同，有时会向最接近的整数四舍五入，继续进行而不报错。

6. 3维（或多维）数据的卷积运算

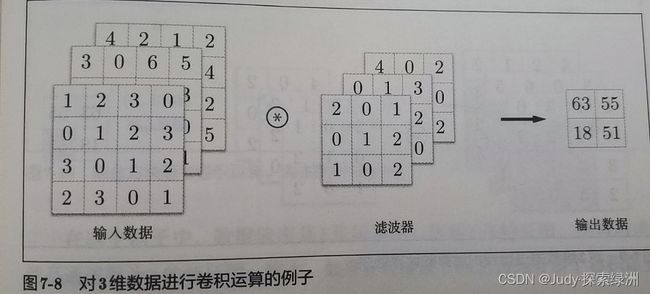
增加通道数，如下图所示。通道方向上有多个特征图时，会按通道进行输入数据和滤波器的卷积计算，并将结果相加，从而得到输出。
注：输入数据和滤波器的通道数要一致。

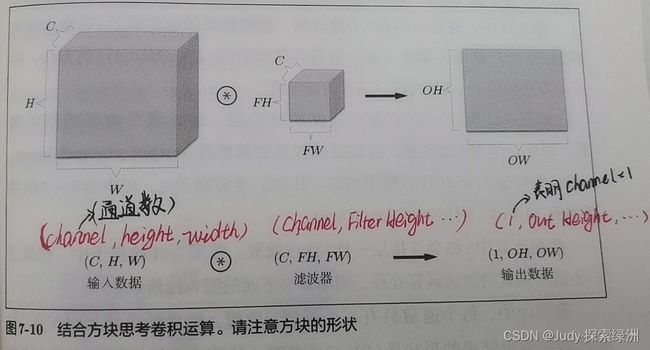
7. 将数据和滤波器结合方块思考

如下图所示：该例中数据的输出是1张特征图，即通道数为1的特征图。

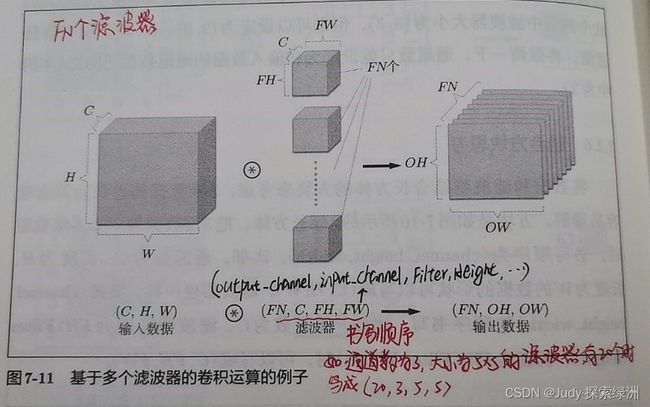
当输出有多个通道时，如下图所示：（仔细观察，手写部分很重要哦！！！）

加偏置时，偏置形状是（FN,1,1）时如下图所示：

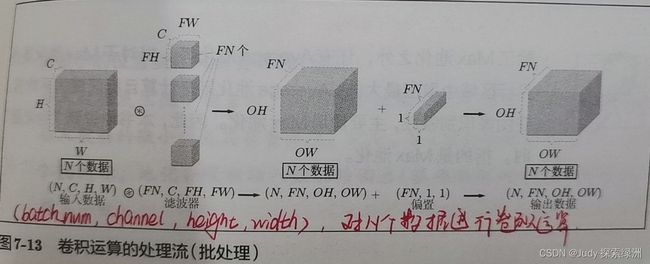
当要进行批处理时，如下图所示：

8. 池化层：

指缩小高、长方向上的空间的运算。如下图所示，将2x2的区域集约成1个元素的处理，缩小空间大小。
Max池化，是获得窗口中最大值的池化，一般池化窗口的大小要和步幅一样。除此之外，还有Average池化：计算窗口（目标区域）平均值。在图像识别领域，一般用Max池化。

池化层特征：
1. 没有要学习的参数；
2. 通道数不发生改变；
3. 对微小位置变化具有鲁棒性（健壮）
输入数据发生微小偏差时，池化层仍会返回相同的结果。

9. 卷积层的实现：

示例：
（9,75）中的9，应该是输出的元素个数。
Im2col实现卷积层的代码:

class Convolution:
    def __init__(self,W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad

    def forward(self,x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1+(H+ 2*self.pad - FH)/ self.stride)  # 第七章计算输出矩阵大小的公式
        out_w = int(1+ (w + 2*self.pad -FW)/ self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad)  # im2col函数，计算卷积层
        col_W = self.W.reshape(FN, -1).T  # 滤波器的展开
        out = np.dot(col, col_W)+ self.b  # 相当于Affine全连接层运算，加偏置的哦
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)  # 更改多维数据矩阵的顺序
        return out

使用reshape（FN，-1），会自动计算-1维度上的元素个数，如：（10,3,5,5）形状的数组的元素个数共有750个，而指定（10，-1）后就会换成（10,75）形状的数组，元素总数也是750个。
Transpose函数会更改多维数组的轴的顺序，如下图所示：

注：在进行卷积层的反向传播时，必须使用im2col的逆处理，可以使用col2im函数，这里，除了要使用这个函数外，卷积层的反向传播和Affine层的实现方式都一样。

9. 池化层的实现

代码实现中，可以使用np.max（x, axis=1）,指在输入x的第一维的各个轴方向上求最大值。
池化层的反向传播backward，可以参考ReLU层的实现中使用的max的反向传播。

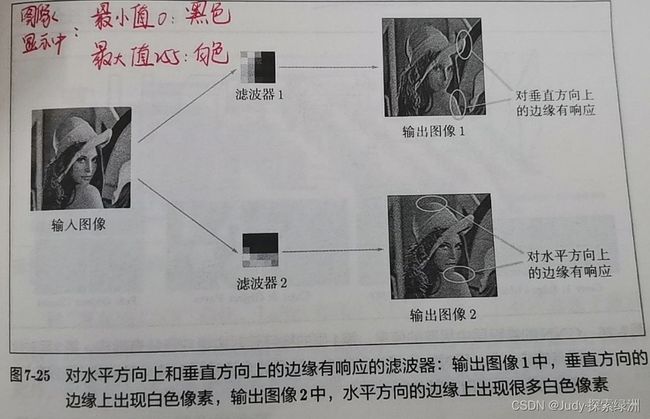
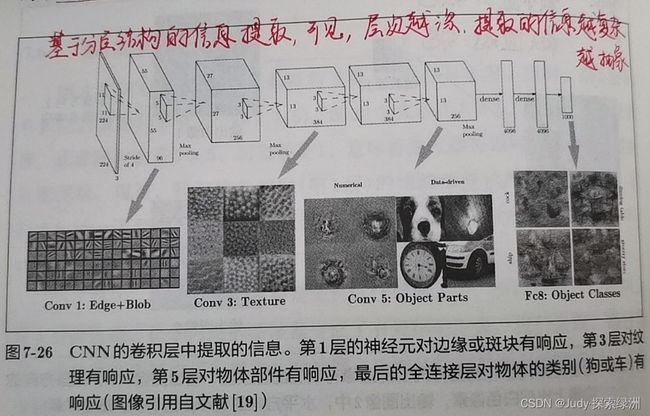
11. CNN的可视化

第一层权重可视化，如下图所示：


LeNet和AlexNet是CNN的代表网络。感兴趣可以自行查阅资料学习。
在深度学习的发展中，大数据和GPU做出了很大贡献。一般跑比较大的数据时，需要用GPU加速。