数据挖掘概念与技术（第三版）课后答案——第五章

未完待续。。。

---

5.1 假定10维基本方体只包含3个基本单元: (1) (a1,d2,d3,d4,...,d9,d10), (2) (d1,b2,d3,d4,...,d9,d10), 和(3) (d1,d2,c3,d4,...,d9,d10),其中a1≠d1, b2≠d2并且c3≠dz。该立方体的度量是count ()。
(a)完全数据立方体中包含多少个非空方体?
(b)完全立方体中包含多少个非空聚集(即非基本)单元?
(c) 如果冰山立方体的条件是“count≥2”,那么冰山立方体包含多少个非空聚集单元?
(d)单元c是闭单元，如果不存在单元d使得d是单元c的特殊化(即d通过用非“*”值替换c中的“*”得到)，并且d与c具有相同的度量值。闭立方体是仅由闭单元组成的数据立方体。该立方体中有多少个闭单元?

（a）n维数据立方体包含个方体，10维数据立方体包含个非空方体。

---

（b）（1）每一个单元生成个非空聚集单元，因此3个基本单元总共有个非空聚集单元（包含重复记录的）；

（2）1×27（即（*，∗，∗，d4，...，d10））重叠两次（因此计数3），3×27（即（d1，∗，∗，d4，...，d10）、（*，d2，∗，d4，...，d10）、（*，∗，d3，d4，...，d10））个像元重叠一次（因此计数2），因此多记录了个单元；

（3）因此包含=个。

---

（c）（1）（d1，∗，∗，d4，...，d9，d10）的计数为2，因为它由单元格2和单元格3生成，

类似地，（2）（∗，d2，∗，d4，...，d9，d10）：2，

（3）（∗，∗，d3，d4，...，d9，d10）：2;

（4）（∗，∗，∗，d4，...，d9，d10）：3

因此该冰山立方体包含个非空聚集单元

---

（d）总共有7个闭单元，如下：

(1) (a1,d2,d3,d4,...,d9,d10) : 1,

(2) (d1,b2,d3,d4,...,d9,d10) : 1,

(3) (d1,d2,c3,d4,...,d9,d10) : 1,

(4) (∗,∗,d3,d4,...,d9,d10) : 2,

(5) (∗,d2,∗,d4,...,d9,d10) : 2,

(6) (d1,∗,∗,d4,...,d9,d10) : 2,

(7) (∗,∗,∗,d4,...,d9,d10) : 3。

5.2 有几种典型的立方体计算方法，如MultiWay[ ZDN97]、 BUC[ BR99] 和Star- Cubing[ XHLW03 ]。简单地描述这三种方法(即用一两行列出要点)，并在以下条件下比较它们的灵活性和性能:

(a)计算低维(例如， 小于8维)、稠密的完全立方体。
(b)计算具有高度倾斜数据分布的大约10维的冰山立方体。
(c)计算高维(例如，超过100维)、稀疏的冰山立方体。

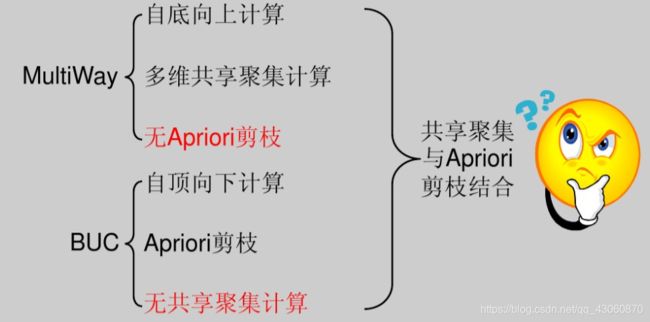
 MultiWay、 BUC 和Star- Cubing总结：

 Star- Cubing：

1. 一种集成自顶向下和自底向上的立方体计算方法，结合了多路数组聚集中的同时聚集和BUC中的Apriori剪枝策略。
2. 利用星型树数据结构进行存储，其中核心的部分就是引入共享维的概念。如果共享维的聚集值不满足冰山条件，则共享维向下的所有单元都不满足冰山条件。

---

（a）MultiWay和Star-Cubing均比BUC的灵活性和性能好。

（b）MultiWay确实适用于冰山立方体。 对于高度倾斜的数据集，Star-Cubing比BUC更好。

（c）MultiWay确实适用于冰山立方体。MultiWay确实适用于冰山立方体。 BUC和Star-Cubing都无法有效地处理高维数据。 应该探索封闭立方体和壳碎片的方法。

5.3假设数据立方体C有d 个维，并且基本方体包含 k个不同元组。
(a)给出一个公式，计算立方体C可能包含的单元的最小个数。
(b)给出一个公式，计算立方体C可能包含的单元的最大个数。
(e)如果每个立方体单元中的计数不能小于阂值v，回答(a)和(b)。
(d)如果只考虑闭单元(使用最小计数阅值v），回答(a) 和(b)。

（a）为了实现最小的个数，我们需要尽可能地“合并”这k个不相同的元组，只有这样在较高层才会有更少的单元（但是在基本方体中总是有k个单元）。我们首先观察两种极端情况：

1、如果当我们删除一个维（记为A），k个元组可以“融合”成一个单元时，这k个元组的形式为：t1=(a1,t'), t2=(a2,t'),..., tk=(ak,t')（其中t'为一个d-1维的元组）。然而，当我们保持属性A，忽略其它属性时却是低效的，因为这时仍然需要维持k个元组，因为k个元组之间无法进行任何合并操作。

 

2、在第一种情况中，只有忽略维A时才会发生“数量约减”。我们可以设想一下另一种情况：“约减”是以一种分布式的和“平均”式的方式发生。对于这两种情况的处理，我们看一个例子：

假设我们有一个8（A）*8（B）*8（C）的三维立方体，并且k=8。在第一种情况中，有8个基本单元，1（roll up to all on A）+8+8=17个 2-D单元，1+1+8（(roll up to all on two dimensions other than A)=10 1-D单元，1个0-D单元。考虑第二种情况，在整个立方体的角落中取一个2*2*2的3维子方体，用8个元组对其填充，我们将得到8个基本单元，4+4+4=12个2-D单元（任一维度上的累积会产生4个单元），2+2+2=6个1-D单元，1个0-D单元。因为36=8+17+10+1>8+12+6+1=27，所以情形2比情形1更好。

情形2总是较好的。假如K=4，这时情形1有4个基本单元，1+4+4=9个2-D单元，1+1+4=6个1-D单元，1个0-D单元，所以共有4+9+6+1=20个单元。对于情形2，我们可以建立一个2（B）*2（C）的2维子方体：4个基本单元，2+2+4（roll up to all on A）=8个2-D单元，1（roll up to all on B and C）+2+2=5个1-D单元，1个0-D单元，共4+8+5+1=18个单元。

对于这一问题的理解，可以按照一种启发式的思路考虑：我们想把k个不同的元组放入一个a*b*c的子方体中，在情形1中是以1*1*k的方式，情形2中是很明显，a+b+c是1-D单元的数量，求1-D方体的最小数量，我们可以将其转化为给定条件abc=k时，求a+b+c的最小值。

综上所述，当我们把所有的k个元组放入一个x1*x2*....*xD的子方体，并且x1x2...xD=k（或者放宽条件将“=”改为“>=”）时，方体包含的单元的个数最小。单元的总数为：

（b）单元个数最大的情况是：k个元组是完全“不相关的”或者“随机的”，即任意两个元组（t11,t12,...,t1D）和（t21,t22,...,t2D）只有忽略所有项才能合并，即：t1i≠t2i,i=1,2,...,D。这时，不管我们如何选择忽略的维，都会产生k个元组，除非忽略所有的维。所以包含单元的最大个数为：

（c）1.最少情况：将k个元组放在在一个完全相同的基本单元中。因此，当所有k个元组都在一个基本单元时，共产生个单元。

2.最大情况：我们如果用（因为我们最多可以得到个基本方体），按照（b）的方法可得到最终结果

（d）通过（c）的分析，因为在这里只要调整k使k满足:k>=v，那么阈值v可以不用考虑。因此，为方便起见，我们将不考虑阈值v。

1.最少情况：如果我们把所有k个元组都放入一个基本单元中，那么闭单元的个数最少为1。

2.最大情况：给定一个p元组{t1,t2,...,tp}，那么最多有一个闭单元。这样,我们可以得到上界

思路：假设有一个2*2*....*2的k维方体，则k个元组基于如下坐标系分布：t1=(1,0,...,0),t2=(0,1,0,...,0),...,tk=(0,0,0,...,0,1)。则（*1,*2,...,*p,0,...,0）是一个闭方体单元（因为把任意一个*变为0或1会导致计数变为p-1或1）。所以一共有2^k-1个闭方体单元。注意到这种情况下k<=D。

5.4假定基本方体有三个维A、B、C,其单元数如下:IAI =1 00000, IBI=100, ICI= 1000。假设每个维平均地分块成10部分。
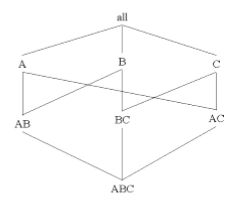
(a) 假定每个维只有一层，绘制完整的立方体的格。
(b)如果每个立方体单元存放一个4字节的度量，若立方体是稠密的，那么所计算的立方体有多大?
(c) 指出空间需求量最小的块计算次序，并求出计算二维平面所需要的内存空间。

（a）

（b）

---

• all: 1

• A: 1,000,000; B: 100; C: 1, 000; subtotal: 1,001,100

• AB: 100,000,000; BC: 100,000; AC: 1,000,000,000; subtotal: 1,100,100,000

• ABC:100,000,000,000

• Total: 101,101,101,101 cells × 4 bytes = 404,404,404,404 bytes

---

（c）计算顺序：B——C——A，如图所示：

二维平面所需的最小内存空间：total =100*1,000（用于整个BC平面）+ 100,000*100（用于AB平面的一行） + 100*100,000（用于AC平面的一块）= 20,100,000 cells = 80,400,000 bytes

5.5通常， 大型数据方体中的许多单元的聚集度量count值为零，导致巨大的、稀疏的多维矩阵。
(a) 设计一种实现方法，它能够很好地克服稀疏矩阵问题。注意，需要详细地解释你的数据结构，讨论空间需求，并解释如何从你的结构中检索数据。
(b)修改你在(a) 中的设计，以便处理增量数据更新。给出新设计的理由。

（a）克服稀疏矩阵问题的一种方法是使用多路数组聚合。

1. 将基于数组的多维数据集划分为足够小的块或子多维数据集，以适合用于多维数据集计算的内存。 首先压缩这些块中的每个块，以删除不包含任何有效数据的单元，然后将其作为对象存储在磁盘上。 为了存储和检索，可以将“ chunkID +offset”作为单元的寻址机制。
2. 涉及通过以最小化每个单元必须重新访问的次数的顺序访问多维数据集单元来计算聚合，从而减少内存访问和存储成本。通过根据数据立方体的大小按升序对它们进行第一次排序和计算，可以将一个较小的平面保留在主内存中，而一次只能为一个较大的平面一次获取和计算一个块。

（b）为了处理增量数据更新，首先按照（a）中所述计算数据多维数据集。 随后，仅重新计算包含具有新数据的单元的块，而无需重新计算整个多维数据集。 这是因为，随着增量更新，一次只能影响一个块。 重新计算的值需要传播到其相应的更高级别的长方体。 因此，可以有效地执行增量数据更新。

5.6在计算高维数据立方体时，遇到固有的维灾难问题:存在大量维组合的子集。
(a)假设在100维的基本方体中只有两个基本单元 {(a1,a2,a3,...,a100), (a1,a2,b3,...,b100)},。计算非空聚集单元数。讨论计算这些单元所需要的空间和时间。
(b) 假设要从(a) 的基本立方体计算冰山立方体。如果冰山条件中的最小支持度计数为2,那么该冰山立方体有多少个聚集单元?给出这些单元。
(c) 引进冰山立方体减轻了计算数据立方体中平凡聚集单元的负担。然而，即便使用冰山立方体，仍然不得不计算大量平凡的、无意义的单元( 即具有小计数的单元)。假设数据库有20个元组，它们映射到(或涵盖)如下两个100维基本方体的单元，每个单元的计数均为{(a1,a2,a3,...,a100) : 10, (a1,a2,b3,...,b100) : 10}。
i.令最小支持度为10。有多少个不同的聚集单元具有如下形式: {(a1,a2,a3,a4,...,a99,∗) : 10, ..., (a1,a2,∗,a4,...,a99,a100) : 10, ..., (a1,a2,a3,∗,...,∗,∗) : 10}?
i.如果忽略所有可以通过用“*”替换某个常量而保持相同的度量值得到的聚集单元，还剩下多少个不同的单元?是哪些单元?

（a）每个基本单元生成个聚合单元。（例如，我们减去1，因为（a1，a2，a3，...，a100）不是聚合单元，是基本单元。）因此，两个基本单元生成个聚合单元，但是，这些单元中有4个是记录2次。这四个单元分别是（a1，a2，∗，...，∗），（a1，∗，...，∗），（∗，a2，∗，...，∗）和（∗，∗，.. .，∗）。 因此，产生的非空聚集单元总数为个。

---

（b）总共4个，分别为：{(a1,a2,∗,...,∗), (a1,∗,∗,...,∗), (∗,a2,∗,...,∗), (∗,∗,∗,...,∗

---

（c）i 如上（a）所示，将有个。

（c）i只剩下三个不同的单元：{（a1，a2，a3，...，a100）：10，（a1，a2，b3，...，b100）：10，（a1，a2，∗，...，∗）：20 }，也就是说在个不同的基本和聚集单元中，只有3个实际提供有价值的信息。              例如：（a1，∗，∗，...，∗）：20可以由（a1，a2，∗，...，∗）：20导出，                                                          （a1，∗，∗，...，a100）：10可以由（a1，a2，a3，...，a100）：10导出。

5.7 提出一种有效地计算闭冰山立方体的算法。

例如，如果我们有三个基本元组（a1，b1，c1），（a1，b2，c1），（a1，b1，c3），则（a1，b1，*）的覆盖率= {（a1， b1，c1），（a1，b1，c3）}。如果具有相同覆盖的单元共享相同的度量，则可以将它们归为同一类。每个类都有一个上限，下限由该类中最具体的单元组成，下限由该类中最普通的单元组成。封闭单元的集合对应于组成该多维数据集的所有不同类的上限。我们可以通过遵循深度优先的搜索策略来计算类：首先查找单元格的上限（∗，∗，...，∗）。让构成该边界的单元格为u1，u2，...，uk。然后，我们专门化每个ui（将值分配给∗维）并递归地找到其上限。找到上限将取决于度量。例如，如果度量是计数，那么如果所有基本单元在维中共享相同的值，则可以通过将*实例化为值v来找到上限。对于上面的示例，（∗，b1，∗）的上限为（a1，b1，∗）。纳入冰山条件并非难事。例如，如果我们有一个反单调条件，例如count（*）> k，则当达到不满足该条件的上限时，可以停止递归。

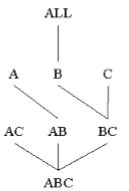
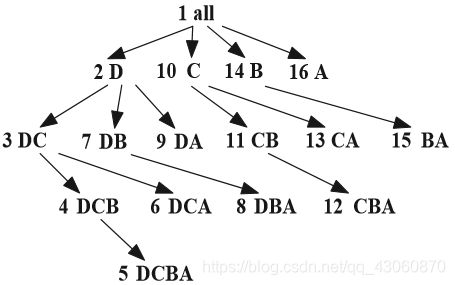
 5.8 假设计算维A、 B、C、D的冰山立方体，其中希望物化满足最小支持度计数v的所有单元，并且维的基数满足cardinality(A) < cardinality(B) < cardinality(C) < cardinality(D)。显示构造以上冰山立方体的BUC处理树(该树显示BUC算法从all开始考察数据立方体格的次序)。

我们知道应该按基数递减的顺序处理维，即首先使用最有区别的维，以期希望我们能够尽快修剪搜索空间。 在这种情况下，我们应该以D，C，B，A的顺序计算立方体，遍历顺序下图所示。

5.9 讨论如何扩展Star-Cbing算法计算冰山立方体、其中冰山条件测试avg不大于某个值v。 

代替使用平均值，我们可以使用每个单元的底部k平均值，它是反单调的。如果一个单元格的最低k平均值大于v，则可以确定没有后代单元格（尺寸较小的单元格）的最低k平均值可以小于v。为了减少检查底k平均条件所需的空间量，我们可以存储一些统计信息，例如落在一定范围v之间的基本元组的计数和总和（例如，小于v，[1.0-1.2)乘以v，[1.2-1.4）乘以v等），然后使用这几个值进行修剪。

5.10 旅行代理的航班数据仓库包含6个维: traveler、departure(city)、departure_time、arrival、arrival_time和flight,两个度量: count()和 avg_fare(),其中avg_fare()在最低层存放具体费用，而在其他层存放平均费用。
(a)假设该立方体是完全物化的。从基本方体[traveler、departure、departure_time、arrival、arrival_time]开始，为了列出2009年每个从洛杉矶乘坐美国航空公司(AA) 的商务旅客的月平均费用，应该执行哪些OLAP操作(例如，上卷flight到airline)?
(b)假设想计算数据立方体，其中条件是记录的个数最少为10,并且平均费用超过500美元。勾画一种有效的 立方体计算方法(基于航班数据分布的常识)。

（a）The OLAP operations are:

• i. roll-up on traveller to the level of category and dice on “business”
• ii. roll-up on departure to the level of city and dice on “L.A.”
• iii. roll-up on departure_time to the level of “ANY” (∗)
• iv. roll-up on arrival to the level of “ANY” (∗)
• v. roll-up on arrival_time to the level of “ANY” (∗)
• vi. roll-up on flight to the level of company and dice on “AA”
• vii. drill-down on traveller to the level of individual
• viii. drill-down on departure_time to the level of month.

（b）有两个约束：min_sup = 10和avg_fare>500。使用冰山立方体算法，例如BUC。 由于avg_fare> 500不是反单调的，因此应将其转换为top-k-avg，即。使用分箱+min_sup修剪立方体的计算量。

5.11 (实现项目)有四种典型的数据立方体计算方法: MuliWey[ ZDN97]、BUC BR99、H ouing[ HP.
DW01]和Star- cubing[ XHLW03]。 

(a)从这些立方体计算算法中任选一种加以实现， 并介绍你的实现、实验和性能。找另外一个在相同平台(如Limux 上C+ +)实现不同算法的学生，比较你们的算法性能。
输人:
i.一个n维基本方体表(n<20)， 它本质上是一个具有n个属性的关系表。
ii.冰山条件count(C)≥k,其中k是一个正整数，作为参数。
输出:
i.计算满足冰山条件的方体的集合，按产生的次序输出。
i.用如下形式汇总方体的集合“方体ID:非空单元数”，按方体字母次序排序，例如A: 155,AB: 120, ABC: 22, ABCD: 4, ABCE: 6, ABD: 36， 其中，“:”后的数表示非空单元数，(这用来快速检查你的结果的正确性。)
(b)基于你的实现，讨论如下问题:
i.随着维数增加，遇到的挑战性计算问题是什么?
i.冰山立方体计算如何对某些数据集解决(a)中的问题?描述这些数据集的特性。
i.给出一个简单的例子，表明冰山立方体有时不能提供好的解决方案。
(c)替代计算高维数据立方体，可以选择物化仅含少数维组合的方体。例如，对于30维的数据立方体，可以对于所有可能的5维组合，只物化5维方体。结果方体形成一个外壳立方体。讨论修改你的算法进行这种计算的难易程度。

（a）无标准答案，自行发挥。

（b） i.立方体的长方体数量与尺寸数量成指数增长。 如果维数增加，则需要大量内存和时间来计算所有方体。

ii.冰山立方体通过消除统计上不重要的聚合单元，可以大大减少聚合单元的数量，从而大大减少了计算量。 如果数据集稀疏但不偏斜，则可以最大程度地提高冰山一角的收益。 这是因为在这些数据集中，除了由少量维组成的方体之外，单元格聚集到同一聚合单元格的可能性相对较低。 因此，许多单元格的值可能小于阈值，因此将被修剪。

iii.例如，考虑一个由100个维度组成的OLAP数据库。 令ai,j为维度i的第j个值。 假设基本长方体中有10个单元格，所有这些单元格都聚集到该单元格上（a1,1 ，a2,1 ，...，a99,1 ，*）。 设支持阈值为10。然后，该单元的所有299个后代单元都满足该阈值。 在这种情况下，无法从修剪效果中受益。

（c）如果采用自顶向下方法，则很容易修改算法。 以BUC为例。 我们可以修改算法以生成特定数量的维组合的壳立方，因为它从顶点（所有）长方体向下进行。 达到最大尺寸数时，可以停止该过程。 可以类似的方式修改H-cubing和Star-cubing。但是，多路数组聚合（MultiWay）难以修改，因为它可以同时计算每个长方体。

5.12 为了样本数据(例如调查数据)的多维分析，提出了抽样立方体。在许多实际应用中，样本数据都可能是高维的( 例如，超过50维的调查数据并不罕见)。
(a)如何为大型样本数据集构造有效的、可伸缩的高维抽样立方体?
(b) 为这种高维抽样立方体设计一个有效的增量更新算法。
(c)讨论如何支持高质量的下钻，尽管某些低层单元可能为空或对可靠的分析而言包含的数据太少。

（a）

方法1：方体内查询拓展：最佳候选应该是与度量值（待预测的值）不相关或者弱相关的那些维。选择用于拓展的维之后，选择这些维中语义类似的值，使得改变最终结果的风险最小。确保新的样本与查询单元中已有的样本具有“相同的”立方体度量值（例如，平均收入）。方法例如：t-检验。

方法2：方体间查询拓展：例如，k维方体在方格中有k个直接父母，其中每个都是（k-1）维的。与方体内拓展一样，方体间拓展也不允许使用相关的维。在不相关的维中，可以进行两个样本的t-检验，以便确定父母与查询单元具有相同的样本均值。如果多个父母通过该检验，则可以逐渐提高置信水平，直到只有一个通过为止。或者也可以同时使用多个父母单元来提升置信度。

（b）

（c）

5.13 排序立方体是为了关系数据库系统中top-k (排序)查询的有效计算而提出的。最近，研究人员提出了另一种类型的查询，称为轮廓线查询( skyline quries)。轮廓线查询返回不受任何其他对象p支配的所有对象p，其中支配定义如下:令P在维d上的值为(p，d)，我们说p被p支配，当且仅当对于每个偏爱的维d，有o(p，d)≤v(p， d),并且至少有一个维d使得等号成立。
(a) 设计一个排序立方体，使得轮廓线查询可以有效地处理。
(b)对于某些用户而言，轮廓线查询有时太严格，并非他们所期望的。可以把轮廓线概念推广到广
叉轮廓线:给定一个d维数据库和- - 个查询q，广义轮廓线( generalized skyline)是如下对象的
集合: (1) 轮廓线对象; (2)轮廓线对象的8 -近邻的非轮廓线对象，其中r是一个轮廓线对
象ρ的e-近邻，如果r与p之间的距离不超过eo设计一个排序立方体，有效地处理广义轮事
线查询。

 

5.14 排序立方体是为了支持关系数据库系统中top-k (排序) 查询面设计的。然面，也可以对数据仓库提出排序查询，其中排序是在多维聚集上，而不是在基本事实的度量上进行。例如，考虑正在分析销售数据库的产品经理。销售数据库存储全国范围的销售历史，按lcaion和time组织。为了进行投资决策，经理可能提出如下查询:“具有最大总产品销售的top-10个(state, year) 单元是哪些?”然后，他可能下钻，进一步问“op-10个 (eiy, month) 单元是哪些?”假设系统能够进行这种部分物化，导出如下两种类型的物化方体:定向方体(eiding eboid)和支持方体(opprting cboid),其中前者包含些提供指导排序处理的简明的高层数据统计量的单元， 而后者提供支持有效联机聚集的倒排表的单元。
(a)设计一种有效计算这种聚集排序立方体的方法。
(6)扩展你的框架，处理更高级的度量。一个可能的例子如下:考虑-个组织捐赠数据库，其中国帽者按age、income 和其他属性分组。感兴趣的症期包括“哪些年龄和收入分组是lopk个最萧捐赠组?”和“哪些捐赠者收入分组具有最大(V)未准差?”  

 

5.15预测立方体 是一个很好的立方体空间多维数据挖掘色例子。ded adlade 见好er
(a) 提出一种有效算法，在给定的多维数据库中计算预测立方体。
(b)你的算法可以使用何种分类模型。解释原因。

 

5.16多特征立方体允许我们基于相当复杂的查询条件构造感兴趣的数据立方体。将如下查询转换成本书介绍的查询形式，你能为这些查询构造多特征立方体吗?
(a)构造一个聪明购物者立方体，其中，--位购物者是聪明的，如果她每次购买的商品至少有10%
是降价出售的。
(b)为最划算的产品构造个数据立方体， 其中，最划算的产 品是那些产品，对它们而言，在给定
的月份售价最低。

 

 5.17发现驱动的立方体探查 是一种在数据立方体的大量单元中标记关注点的可取方法。对于一个点是否应该视为有趣的，值得标记，每个用户都可能有不同的看法。假设一个人想要标记这些对象，其z分数绝对值在d维平面的每行每列都大于2。
(a)设计-一种有效的计算方法，在数据立方体计算时识别这样的点。
(b)假设部分物化的方体有(d-1)维和(d+1) 维方体，但是没有d维方体。设计一种方法标记这样的(d-1)维单元，其d维子女包含这种标记的点。