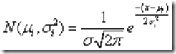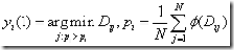毕业了,毕业论文也可以拿来晒晒了。觉的自己的论文涉及的知识点特别多,用到了很多图像处理和机器学习方面的技术。第三章主要是讲的颜色聚类的方法用来提取自然场景文本的候选连通域。(工作了时间不是很多,先把文章发上来,一周之内在好好拓展并整理).
一、颜色聚类的优点
分析自然场景文本的特点可得,在一个文本区域内部,一般一个字符内部的颜色变化不大。对于一幅24位RGB彩色图,需要处理的颜色范围达到 。显然,大范围、高精度的颜色对于文本定位来说是没有必要的,所以本章先用颜色聚类的方式来缩小颜色空间的范围,增大各个颜色间的距离,以便于后续连通域提取。
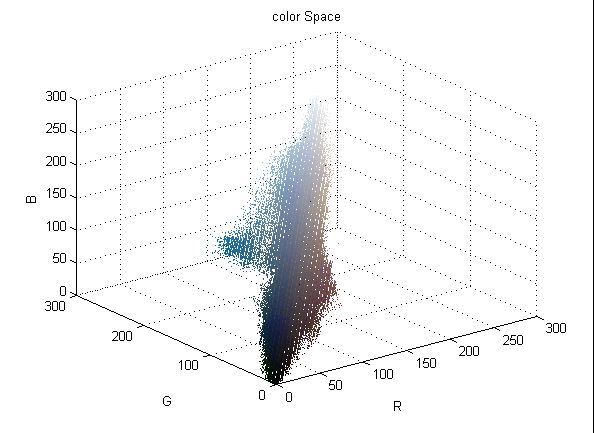
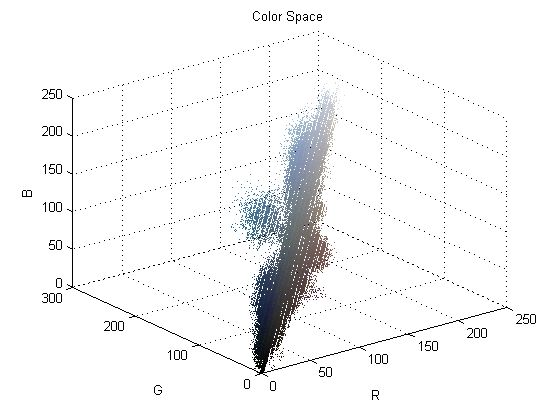
如图3. 2所示图(a)是原图,图(b)是对应的RGB颜色空间三维散点图,图(c)是聚类后的图像,图(d)是图(c)对应的散点图,图(a)中文本和背景的颜色混成一团难以分割,而图(d)中可以明显看到两部分不同的颜色团的间隙,而这两部分颜色分别对应的是文本和背景。目前颜色聚类的方法有很多,不同的方法适用于解决不同的问题。下面首先分析对比了目前主流的方法,然后从效果、时间、参数设定等各个方面考虑,选取适用于文本定位的方法。 (a) 原图 (b) 图(a)的颜色散布图 (c) 图(a)聚类后的图 (d) 图(c)的颜色散布图 图3. 2聚类增大颜色距离示意图。
二、 颜色聚类方法
聚类是对数据的一种聚集,是将类似的数据聚成一类。聚类是一种无监督的分类方式,其优点在于不需要预先的训练过程。目前比较常用的聚类方式有K-means,混合高斯模型 (Gaussian Mixture Models,GMM),Mean shift等。
1. K-means算法
K-means是比较简单又常用的聚类算法,k表示的是聚类中心的个数,每个类是由相应的聚类中心来表示。K-means算法包括四个步骤:
(1) 随机选择初始的聚类中心。
(2) 把每个目标分配给最近的中心(最近的度量指的是目标到中心的欧式距离)。
(3) 根据上一步聚好的类,重新计算聚类中心(所有点到上一步中心的平均值)。
(4) 重复(2)直到聚类中心不再发生变化。 K-means 的优点是简单快速并且能够很容易的实现,其缺点是K值需要人工设定,另外对于离群点太过敏感。
2. GMM算法
GMM用于聚类是基于这样的假设即数据空间的数据是由多个高斯模型生成的。GMM解决的问题是根据数据空间的数据来估计多个高斯模型的参数,然后根据这些参数确定高斯模型[33]。一旦高斯模型确定了,那么数据的聚类中心也就确定了。
假设数据空间中的数据符合高斯混合模型即:
其中 ![]() 是聚类中心的个数,
是聚类中心的个数, ![]() 代表的是高斯模型之间的权值并且符合
代表的是高斯模型之间的权值并且符合![]() 。其中
。其中 ![]() 符合下式:
符合下式:
其中 ![]() 和
和 ![]() 分别代表的是第
分别代表的是第 ![]() 个聚类中心的均值和方差。那么需要根据数据来估计GMM的参数为
个聚类中心的均值和方差。那么需要根据数据来估计GMM的参数为![]() 。估计GMM的参数的算法为EM算法。EM算法分为两步,在E步假设参数
。估计GMM的参数的算法为EM算法。EM算法分为两步,在E步假设参数![]() 是已知的,根据最大似然来估计每个高斯模型的权值。在M步对E步得到的结果重新估计参数,然后不断迭代地使用EM步骤,直到收敛。
是已知的,根据最大似然来估计每个高斯模型的权值。在M步对E步得到的结果重新估计参数,然后不断迭代地使用EM步骤,直到收敛。
GMM用于聚类的优点是最后得到的结果是数据属于某个类的概率,其缺点是要先确定聚类中心的个数。
3. Mean shift算法
Mean shift的目标是根据给定的数据寻找概率密度的局部最大值。Mean-shift主要包括四个步骤:
(1) 随机选择若干个感兴趣区域。
(2) 计算感兴趣区域数据的中心 。
(3) 移动区域到新的中心。
(4) 不断计算直到收敛。
Mean shift的数学定义如下:
其中, ![]() 为核函数加权下的Mean shift代表的是均值向量移动的方向,
为核函数加权下的Mean shift代表的是均值向量移动的方向, ![]() 是感兴趣区域的中心,
是感兴趣区域的中心, ![]() 表示的是核函数,
表示的是核函数, ![]() 表示的是带宽。在算法中,首先确定Mean shift的起点为感兴趣区域的中心
表示的是带宽。在算法中,首先确定Mean shift的起点为感兴趣区域的中心 ![]() ,然后计算Mean shift 向量的终点式3.3中的第一项。然后将感兴趣区域的中心移动到向量的终点,重新计算Mean shift,当式(3.4)满足时,结束移动,这时中心就收敛到数据空间中局部最大值。
,然后计算Mean shift 向量的终点式3.3中的第一项。然后将感兴趣区域的中心移动到向量的终点,重新计算Mean shift,当式(3.4)满足时,结束移动,这时中心就收敛到数据空间中局部最大值。
Mean shift的思想是将数据点分配给隐含概率密度函数的某个模型。它的优点是聚类的类别数不需要预先知道并且聚类的结构可以是任意的,它的缺点是计算复杂度太高。
4. Quick shift算法
Quick shift是由Mean shift改进而来的。Quick shift改进了计算复杂度太高这一缺点,它不需要使用梯度来寻找概率密度的模式,而仅仅是将每个点移动到使概率密度增加的最近的点来获得。公式如下:
其中 ![]() 代表的是特征空间中点的下一个位置,
代表的是特征空间中点的下一个位置, ![]() 代表的是两点之间的距离,
代表的是两点之间的距离, ![]() 是核函数,一般选择高斯核函数,
是核函数,一般选择高斯核函数,![]() 是特征空间中点的个数。通过不断移动,所有点连成了一颗树,再通过一定的阈值将树分割成一个森林,这样森林里的每棵树就是一个聚类。特征空间是一个五维空间,包含转换到Lab空间的三个颜色分量和两个空间位置信息。
是特征空间中点的个数。通过不断移动,所有点连成了一颗树,再通过一定的阈值将树分割成一个森林,这样森林里的每棵树就是一个聚类。特征空间是一个五维空间,包含转换到Lab空间的三个颜色分量和两个空间位置信息。
Quick shift继承了Mean shift的优点,不需要指定聚类中心,但同时改进了其速度慢的缺点。