机器学习笔记（七）-主成分分析PCA

原创不易，转载前请注明博主的链接地址：Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境：
运行平台： Windows
Python版本： Python3.x
IDE： PyCharm

一、 前言

解决模型过拟合问题的基本方法有：

• 增加数据量
• 正则化
• 降维
  • 直接降维：人工的特征选择
  • 线性降维：PCA、MDS
  • 非线性降维：流形：ISOMAP，LLE

这次要介绍的内容是高维数据的降维。为什么要降维呢？这里就不得不说一下维度灾难——会导致数据稀疏。举一个简单的几何例子，如下图：

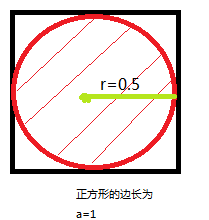
假设有一个D维的边长a=1的超正方体，里面有一个D维的半径为0.5的超球体。则

• V超正方体=1
• V超球体=K0.5^D当D—>+∞时，
  
  出现一个惊人的发现，当D的值足够大，发现中间的超球体的竟然趋近于零。

这样扩展到数据来说，随着数据维度的增大，数据的量也会相对稀疏的多。这就是维度灾难。实际上在许多领域的研究与应用中，为了反映事物的多个变量对结果的影响，需要进行大量数据收集以便进行分析寻找规律。多变量、大样本虽然会为研究和应用提供了丰富的信息，但也遇到了以下问题：

• 一定程度上增加了数据采集的工作量
• 更重要的是在多数情况下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性，同时对分析带来不便。
• 如果分别对每个指标进行分析，分析往往是孤立的，而不是综合的。盲目减少指标会损失很多信息，容易产生错误的结论。

因此需要找到一个合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的 ，由于各变量间存在一定的相关关系，因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析就属于这类降维的方法。

二、 PCA内容讲解

2.1 预备知识

数据集：

样本均值矩阵化表示：

样本协方差矩阵化表示，这里面涉及到一个叫中心矩阵的内容：


有了数据集，数据的均值和协方差，下面给出PCA算法流程
算法输入：数据集Xmxn

• 按列计算数据集X的均值Xmean，然后令Xnew=X−Xmean；
• 求解矩阵Xnew的协方差矩阵，并将其记为Cov；
• 计算协方差矩阵COv的特征值和相应的特征向量；
• 将特征值按照从大到小的排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵Wnxk;
• 计算XnewW，即将数据集Xnew投影到选取的特征向量上，这样就得到了我们需要的已经降维的数据集XnewW。

注意，计算一个nxn矩阵的完整的特征向量分解的时间复杂度为 O(n3) 。如果我们将数据集投影到前 k 个主成分中，那么只需寻找前 k个特征值和特征向量。这可以使用更高效的方法得到,例如幂方法(power method) (Golub and Van Loan, 1996)，它的时间复杂度为 O(kn2)，或者我们也可以使用 EM 算法。

2.2 经典主成分分析

经典主成分分析（Classical Principal Component Analysis）的核心思想：PCA的思想是将n维特征映射到k维上（k
归纳起来可以用一个中心两个基本点来说明（两个基本点服务于一个中心）：

• 一个中心：对原始的特征空间进行重构，将相关变成无关：比如发放信用卡的特征集中有年龄、姓名、学位、学历。其中一般认为学历和学位是相关的，接下里的目的就是要让相关变成无关。
• 最大投影方差基本点，如下图：
  
  将样本投影到u1和u2上的距离D1>D2，则u1这个特征相对于u2来说就是主成分。最大投影方向就是主成分。
• 最小重构距离：还看上图，如果把样本点投影到u1和u2后，再将样本点还原原来的数据，这样的代价，显然u1比u2小的多。（因为u1相对稀疏比较好还原，u2甚至有些点都已经重合了，不容易还原）

2.3 最大投影方差

首先要对数据进行中心化处理，为什么要进行中心化处理呢？因为主成分变换对正交向量的尺度敏感。数据在变换前需要进行归一化处理。 然后计算投影方差，接着可以将上一步的待求内容转化为最优化问题吹，最后通过拉格朗日函数，将约束项放到最优化问题中，通过极大似然求得最优解。


在式子：

这样就可以得出一个重要结论最大的主成分实际上就是协方差矩阵S，对它进行特征值分解，它的特征向量就是主成分。

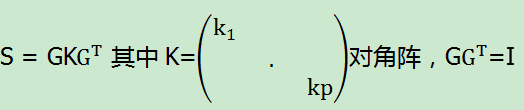
如果要选取k个主成分，只需要选取前k个对角矩阵的值（k

2.4 最小重构代价

有了上面最小重构代价的思想，接下来直接可以给出运算过程：

2.5 奇异值分解SVD

上面去主成分的方法实现是太麻烦了，有没有更简单的方法呢？？？？答案是肯定的，那就是奇异值分解SVD！！！！！！！！！
首先特征值和特征向量的定义如下：

其中A是一个n×n的实对称矩阵，x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x是矩阵A的特征值λ所对应的特征向量。
求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值λ1≤λ2≤…≤λn,以及这n个特征值所对应的特征向量{w1,w2,…wn}，，如果这n个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示：

其中W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。这样我们的特征分解表达式可以写成：

注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时就要用到奇异值分解SVD。
SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设矩阵A是一个m×n的矩阵，那么定义矩阵A的SVD为：

其中U是一个m×m的列正交矩阵；Σ是一个m×n的对角矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值；V是一个n×n的正交矩阵。U和V都是酉矩阵，即满足：


这样可以求出每个奇异值，进而求出奇异值矩阵Σ。

三、 PCA的Python实现

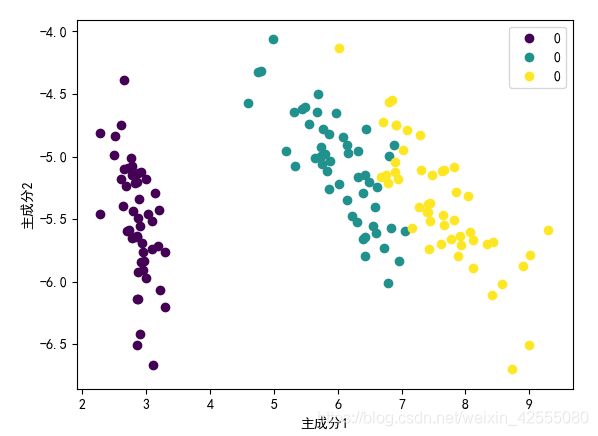
此次选用的依然是Python内置的iris数据集，通过PCA降维，对数据分类：

from __future__ import print_function
from sklearn import datasets
import matplotlib.pyplot as plt
from pylab import *
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import numpy as np

def shuffle_data(X, y, seed=None):
    if seed:
        np.random.seed(seed)
    idx = np.arange(X.shape[0])
    np.random.shuffle(idx)
    return X[idx], y[idx]

# 正规化数据集 X
def normalize(X, axis=-1, p=2):
    lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
    lp_norm[lp_norm == 0] = 1
    return X / np.expand_dims(lp_norm, axis)

# 标准化数据集 X
def standardize(X):
    X_std = np.zeros(X.shape)
    mean = X.mean(axis=0)
    std = X.std(axis=0)
    # 做除法运算排除分母不能等于0的情形
    for col in range(np.shape(X)[1]):
        if std[col]:
            X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
    return X_std

# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
    if shuffle:
        X, y = shuffle_data(X, y, seed)

    n_train_samples = int(X.shape[0] * (1-test_size))
    x_train, x_test = X[:n_train_samples], X[n_train_samples:]
    y_train, y_test = y[:n_train_samples], y[n_train_samples:]
    return x_train, x_test, y_train, y_test

# 计算矩阵X的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
    if not Y.any():
        Y = X
    n_samples = np.shape(X)[0]
    covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
    return np.array(covariance_matrix, dtype=float)

# 计算数据集X每列的方差
def calculate_variance(X):
    n_samples = np.shape(X)[0]
    variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
    return variance

# 计算数据集X每列的标准差
def calculate_std_dev(X):
    std_dev = np.sqrt(calculate_variance(X))
    return std_dev

# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
    # 先计算协方差矩阵
    covariance_matrix = calculate_covariance_matrix(X, Y)
    # 计算X, Y的标准差
    std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
    std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
    correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))

    return np.array(correlation_matrix, dtype=float)

class PCA():
    """
    主成份分析算法PCA，非监督学习算法.
    """
    def __init__(self):
        self.eigen_values = None
        self.eigen_vectors = None
        self.k = 2

    def transform(self, X):
        """ 
        将原始数据集X通过PCA进行降维
        """
        covariance = calculate_covariance_matrix(X)

        # 求解特征值和特征向量
        self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)

        # 将特征值从大到小进行排序，注意特征向量是按列排的，即self.eigen_vectors第k列是self.eigen_values中第k个特征值对应的特征向量
        idx = self.eigen_values.argsort()[::-1]
        eigenvalues = self.eigen_values[idx][:self.k]
        eigenvectors = self.eigen_vectors[:, idx][:, :self.k]

        # 将原始数据集X映射到低维空间
        X_transformed = X.dot(eigenvectors)

        return X_transformed

if __name__ == "__main__":
    #使用燕尾花数据集
    data = datasets.load_iris()
    X = data.data
    y = data.target

    # 将数据集X映射到低维空间
    X_trans = PCA().transform(X)

    x1 = X_trans[:, 0]
    x2 = X_trans[:, 1]

    cmap = plt.get_cmap('viridis')
    colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]

    class_distr = []
    # 展示不同类别数据的分布
    for i, l in enumerate(np.unique(y)):
        _x1 = x1[y == l]
        _x2 = x2[y == l]
        _y = y[y == l]
        class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))

    # Add a legend
    plt.legend(class_distr, y, loc=1)

    # Axis labels
    plt.xlabel('主成分1')
    plt.ylabel('主成分2')
    plt.show()

结果：

四、 总结

PCA优缺点并存：

• 优点：

  • 它是无监督学习，完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。
  • 用PCA技术可以对数据进行降维，同时对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
  • 各主成分之间正交，可消除原始数据成分间的相互影响。
  • 计算方法简单，易于在计算机上实现。

• 缺点：

  • 如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。
  • 贡献率小的主成分往往可能含有对样本差异的重要信息。
  • 特征值矩阵的正交向量空间是否唯一有待讨论。
  • 在非高斯分布的情况下，PCA方法得出的主元可能并不是最优的，此时在寻找主元时不能将方差作为衡量重要性的标准。

这篇博文主要介绍了，PCA主成分分析。首先通过几何概念引出维度爆炸带来的问题，接下来通过PCA数据降维来解决之。在主讲PCA内容时主要介绍了：经典主成分分析、最大投影方差、最小重构距离，SVD奇异值分解。最后通过Python实现PCA。这篇文章就到这里了，欢迎大佬们多批评指正，也欢迎大家积极评论多多交流。
　

　

参考文章

1 主成分分析（PCA）原理详解
2 奇异值分解(SVD)原理与在降维中的应用*****
3 数据降维方法及Python实现
4 主成分分析PCA*****
5 详解主成分分析PCA
6 主成分分析（PCA）一次讲个够*****
7 奇异值分解（SVD）理论与python实现用于图片压缩*****