降维笔记-主成分分析
补充知识:
- 方差 v a r ( X ) = E ( ( X − E ( X ) 2 ) var(X) = E((X - E(X)^2) var(X)=E((X−E(X)2)
- 协方差 c o v ( X , Y ) = E ( ( X − E ( X ) ) ( Y − E ( Y ) ) ) cov(X, Y) = E((X - E(X))(Y - E(Y))) cov(X,Y)=E((X−E(X))(Y−E(Y)))
- 相关系数 ρ ( X , Y ) = v o c ( X , Y ) v a r ( X ) v a r ( Y ) \rho(X, Y) = \frac{voc(X, Y)}{\sqrt{var(X)var(Y)}} ρ(X,Y)=var(X)var(Y)voc(X,Y)
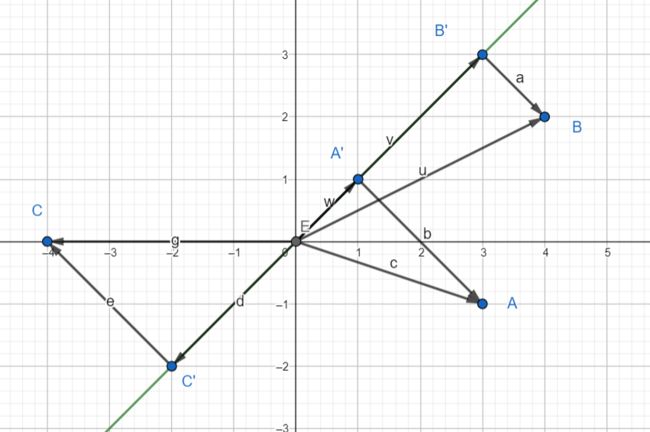
1.思路:主成分分析就是一种降维,要把坐标 ( x 1 , x 2 ) (x_1, x_2) (x1,x2)降维到坐标 ( y 1 , y 2 ) (y_1, y_2) (y1,y2)中的 y 1 y_1 y1;具体的思路就是让下图中的 O A ′ 2 + O B ′ 2 + O C ′ 2 OA'^2 + OB'^2 + OC'^2 OA′2+OB′2+OC′2(方差)最大(图中把原本的三个向量压缩到y = x这一直线上,实际上就是找到一条直线,使上述方差最大)
2.总体主成分:
随机变量: x ⃗ = ( x 1 , ⋯ , x m ) T \vec{x} = (x_1, \cdots, x_m)^T x=(x1,⋯,xm)T
均值向量: μ ⃗ = ( μ 1 , ⋯ , μ m ) T \vec{\mu} = (\mu_1, \cdots, \mu_m)^T μ=(μ1,⋯,μm)T
协方差矩阵: Σ = c o v ( x ⃗ , x ⃗ ) = E ( ( x ⃗ − μ ⃗ ) ( x ⃗ − μ ⃗ ) T ) \Sigma = cov(\vec{x}, \vec{x}) = E((\vec{x} - \vec{\mu})(\vec{x} - \vec{\mu})^T) Σ=cov(x,x)=E((x−μ)(x−μ)T)
将 x ⃗ \vec{x} x映射到 y ⃗ = ( y 1 , y 2 , ⋯ , y m ) T \vec{y} = (y_1, y_2, \cdots, y_m)^T y=(y1,y2,⋯,ym)T
α ⃗ i = ( α 1 i , ⋯ , α m i ) T y i = α ⃗ i x ⃗ = α 1 i x 1 + ⋯ + α m i x m \vec{\alpha}_i = (\alpha_{1i}, \cdots, \alpha_{mi})^T\\ y_i = \vec{\alpha}_i\vec{x} = \alpha_{1i}x_1 + \cdots + \alpha_{mi}x_m αi=(α1i,⋯,αmi)Tyi=αix=α1ix1+⋯+αmixm
可以得到 y ⃗ \vec{y} y的相关数据
{ E ( y i ) = α ⃗ i T μ ⃗ i v a r ( y i ) = α ⃗ i T Σ α ⃗ i c o v ( y i , y j ) = α ⃗ i T Σ α ⃗ j \begin{cases} E(y_i) = \vec{\alpha}_i^T \vec{\mu}_i\\ var(y_i) = \vec{\alpha}_i^T \Sigma \vec{\alpha}_i\\ cov(y_i, y_j) = \vec{\alpha}_i^T\Sigma \vec{\alpha}_j \end{cases} ⎩⎪⎨⎪⎧E(yi)=αiTμivar(yi)=αiTΣαicov(yi,yj)=αiTΣαj
定义主成分:(上述)线性变换满足如下条件
(1) α ⃗ i \vec{\alpha}_i αi是单位向量 α ⃗ i T α ⃗ j = 1 , i = 1 , 2 , ⋯ , m \vec{\alpha}_i^T\vec{\alpha}_j = 1, i = 1, 2, \cdots, m αiTαj=1,i=1,2,⋯,m
(2) y i y_i yi与 y j y_j yj不相关,即 c o v ( y i , y j ) = 0 , ( i ≠ j ) cov(y_i, y_j) = 0, (i \neq j) cov(yi,yj)=0,(i=j)
(3) y 1 y_1 y1是 x ⃗ \vec{x} x所有线性变换中,方差最大的,即 v a r ( y 1 ) var(y_1) var(y1)最大; y 2 y_2 y2与 y 1 y_1 y1不相关,且方差最大……
3.计算主成分:
Σ \Sigma Σ是 x ⃗ \vec{x} x协方差矩阵
Σ \Sigma Σ特征值为 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ m > 0 \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_m > 0 λ1≥λ2≥⋯≥λm>0
对应的单位特征向量为 α ⃗ 1 , ⋯ , α ⃗ m \vec{\alpha}_1, \cdots, \vec{\alpha}_m α1,⋯,αm
则第k主成分是 y k = α ⃗ k T x ⃗ y_k = \vec{\alpha}_k^T \vec{x} yk=αkTx
推论: y ⃗ = ( y 1 , ⋯ , y m ) T \vec{y} = (y_1, \cdots, y_m)^T y=(y1,⋯,ym)T的分量依次是 x ⃗ \vec{x} x的1到m主成分的充要条件为
(1) y ⃗ = A T x ⃗ , A = ( α ⃗ 1 , ⋯ , α ⃗ m ) \vec{y} = A^T \vec{x}, A = (\vec{\alpha}_1, \cdots, \vec{\alpha}_m) y=ATx,A=(α1,⋯,αm),这里 α ⃗ k \vec{\alpha}_k αk为 λ k \lambda_k λk对应的单位特征向量
(2) c o v ( y ⃗ ) = d i a g ( λ 1 , ⋯ , λ m ) , λ 1 ≥ ⋯ , λ m cov(\vec{y}) = diag(\lambda_1, \cdots, \lambda_m), \lambda_1 \geq \cdots, \lambda_m cov(y)=diag(λ1,⋯,λm),λ1≥⋯,λm
4.总体主成分 y ⃗ \vec{y} y的性质
(1) c o v ( y ⃗ ) = Λ = d i a g ( λ 1 , ⋯ , λ m ) cov(\vec{y}) = \Lambda = diag(\lambda_1, \cdots, \lambda_m) cov(y)=Λ=diag(λ1,⋯,λm)
(2) ∑ i = 1 m λ i = ∑ i = 1 m σ i i \sum^m_{i = 1}\lambda_i = \sum^m_{i = 1}\sigma_{ii} ∑i=1mλi=∑i=1mσii,其中 σ i i \sigma_{ii} σii为 x ⃗ \vec{x} x的方差,也就是 Σ \Sigma Σ矩阵的对角线元素
(3)相关系数 ρ ( y k , x i ) \rho(y_k, x_i) ρ(yk,xi)称为因子负荷量
ρ ( y k , x i ) = λ k α i k σ i i \rho(y_k, x_i) = \frac{\sqrt{\lambda}_k\alpha_{ik}}{\sqrt{\sigma_{ii}}} ρ(yk,xi)=σiiλkαik
(4) ∑ i = 1 m σ i i ρ 2 ( y k , x i ) = λ k \sum^m_{i = 1}\sigma_{ii}\rho^2(y_k, x_i) = \lambda_k ∑i=1mσiiρ2(yk,xi)=λk
(5) ∑ k = 1 m ρ 2 ( y k , x i ) = 1 \sum^m_{k = 1}\rho^2(y_k, x_i) = 1 ∑k=1mρ2(yk,xi)=1
(6)贡献率 η k = λ k ∑ i = 1 m λ i \eta_k = \frac{\lambda_k}{\sum^m_{i = 1}\lambda_i} ηk=∑i=1mλiλk
前k个主成分 y 1 , ⋯ , y k y_1, \cdots, y_k y1,⋯,yk对的贡献率
∑ m η i = ∑ i = 1 k λ i ∑ i = 1 m λ i \sum^m\eta_i = \frac{\sum^k_{i = 1}\lambda_i}{\sum^m_{i = 1}\lambda_i} ∑mηi=∑i=1mλi∑i=1kλi
5.主成分个数:如果要取前q个主成分,则用 y ⃗ = A q T x ⃗ \vec{y} = A_q^T \vec{x} y=AqTx,其中 A q A_q Aq是_计算主成分的推论_中的正交矩阵A的前q列
6.规范化变量
思路:为了消除量纲不同造成的方差大小的不一样,令 x i ∗ = x i − E ( x i ) v a r ( x i ) x^*_i = \frac{x_i - E(x_i)}{\sqrt{var(x_i)}} xi∗=var(xi)xi−E(xi),此时协方差矩阵 Σ ∗ \Sigma^* Σ∗就是相关矩阵R,设 e ⃗ 1 ∗ , ⋯ , e ⃗ m ∗ \vec{e}_1^*, \cdots, \vec{e}_m^* e1∗,⋯,em∗是矩阵R的单位特征向量
(1) c o v ( y ∗ ) = Λ ∗ = d i a g ( λ 1 ∗ , ⋯ , λ m ∗ ) cov(y^*) = \Lambda^* = diag(\lambda_1^*, \cdots, \lambda^*_m) cov(y∗)=Λ∗=diag(λ1∗,⋯,λm∗)
(2) ∑ k = 1 m λ k = m \sum^m_{k = 1}\lambda_k = m ∑k=1mλk=m
(3) ρ ( y k ∗ , x i ∗ ) = λ ∗ e i k ∗ \rho(y_k^*, x_i^*) = \sqrt{\lambda^*}e^*_{ik} ρ(yk∗,xi∗)=λ∗eik∗,其中 e i k ∗ e_{ik}^* eik∗在单位特征向量中 e ⃗ k ∗ = ( e 1 k ∗ , ⋯ , e m k ∗ ) \vec{e}_k^* = (e_{1k}^*, \cdots, e_{mk}^*) ek∗=(e1k∗,⋯,emk∗)
(4) ∑ i = 1 m ρ 2 ( y k ∗ , x i ∗ ) = ∑ i = 1 m λ k ∗ e i k ∗ 2 = λ k ∗ \sum^m_{i = 1}\rho^2(y_k^*, x_i^*) = \sum^m_{i = 1}\lambda_k^*e_{ik}^{*2} = \lambda_k^* ∑i=1mρ2(yk∗,xi∗)=∑i=1mλk∗eik∗2=λk∗
(5) ∑ k = 1 m ρ 2 ( y k ∗ , x i ∗ ) = 1 \sum^m_{k = 1}\rho^2(y_k^*, x_i^*) = 1 ∑k=1mρ2(yk∗,xi∗)=1
7.样本主成分分析
X = ( x ⃗ 1 , ⋯ , x ⃗ n ) X = (\vec{x}_1, \cdots, \vec{x}_n) X=(x1,⋯,xn)用n个样本,每个样本m维
样本协方差绝阵 S = [ s i j ] m × n , s i j = 1 n − 1 ∑ k = 1 n ( x i k − x ˉ i ) ( x j k − x ˉ j ) S = [s_{ij}]_{m \times n}, s_{ij} = \frac{1}{n - 1} \sum^n_{k = 1}(x_{ik} - \bar{x}_i)(x_{jk} - \bar{x}_j) S=[sij]m×n,sij=n−11∑k=1n(xik−xˉi)(xjk−xˉj)
其中均值 x ˉ i = 1 n ∑ k = 1 n x i k , x ˉ j = 1 n ∑ k = 1 n x j k \bar{x}_i = \frac{1}{n}\sum^n_{k = 1}x_{ik}, \bar{x}_j = \frac{1}{n} \sum^n_{k = 1}x_{jk} xˉi=n1∑k=1nxik,xˉj=n1∑k=1nxjk
相关矩阵$ R = [r_{ij}]{m \times m}, r{ij} = \frac{s_{ij}}{\sqrt{s_{ii}s_{jj}}}$
同理,主成分的计算如下
y ⃗ = ( y 1 , ⋯ , y m ) T = A T x ⃗ y i = α ⃗ i T x ⃗ A = ( α ⃗ 1 , ⋯ , α ⃗ m ) \begin{aligned} &\vec{y} = (y_1, \cdots, y_m)^T = A^T\vec{x}\\ &y_i = \vec{\alpha}_i^T\vec{x}\\ &A = (\vec{\alpha}_1, \cdots, \vec{\alpha}_m ) \end{aligned} y=(y1,⋯,ym)T=ATxyi=αiTxA=(α1,⋯,αm)
得到方差: v a r ( y i ) = 1 n − 1 ∑ j = 1 n ( α ⃗ i T x ⃗ j − α ⃗ i T x ⃗ ˉ ) = α ⃗ i T S α ⃗ i var(y_i) = \frac{1}{n - 1}\sum^n_{j = 1}(\vec{\alpha}_i^T\vec{x}_j - \vec{\alpha}_i^T\bar{\vec{x}}) = \vec{\alpha}_i^T S\vec{\alpha}_i var(yi)=n−11∑j=1n(αiTxj−αiTxˉ)=αiTSαi
协方差: c o v ( y i , y k ) = α ⃗ i T S α ⃗ k cov(y_i, y_k) = \vec{\alpha}_i^T S \vec{\alpha}_k cov(yi,yk)=αiTSαk
规范化样本: x i j ∗ = x i j − x ⃗ ˉ i s i i x^*_{ij} = \frac{x_{ij} - \bar{\vec x}_i}{\sqrt{s_{ii}}} xij∗=siixij−xˉi
在规范化的样本下:协方差矩阵S = 相关矩阵R = 1 n − 1 X X T \frac{1}{n - 1}XX^T n−11XXT
8.相关矩阵特征值分解算法(规定贡献率g)
(1)规范化数据(为方便表示,规范化的数据省略星号)
(2)相关矩阵 R = [ r i j ] m × m = 1 n − 1 X X T R = [r_{ij}]_{m \times m} = \frac{1}{n - 1} XX^T R=[rij]m×m=n−11XXT
(3)解特征方程 ∣ R − λ I ∣ = 0 |R - \lambda I| = 0 ∣R−λI∣=0,求出特征向量 λ 1 ≥ ⋯ ≥ λ m \lambda_1 \geq \cdots \geq \lambda_m λ1≥⋯≥λm
保留贡献率之和达到g的k个主成分
求出对应单位特征向量 α ⃗ i = ( α 1 i , ⋯ , α m i ) T , i = 1 , 2 , ⋯ , k \vec{\alpha}_i = (\alpha_{1i}, \cdots, \alpha_{mi})^T, i = 1, 2, \cdots, k αi=(α1i,⋯,αmi)T,i=1,2,⋯,k
(4)第i个样本主成分 y ⃗ i = α ⃗ i x ⃗ \vec{y}_i = \vec{\alpha}_i\vec{x} yi=αix
注:普遍的理解是,我们先确定贡献率然后再确定到底保留多少个主成分,但是再sklearn实际应用的过程中是确定保留多少个主成分,然后才能用explained_variance_ratio_看这些主成分的贡献率是多少
而且在实际使用的过程中,哪怕是高维的向量,一般前几个主成分就可以达到99%的贡献率,贡献率并不能完全反映对信息的保留程度
9.奇异值主成分分析算法
思路:协方差 S = 1 n − 1 X X T = X ′ T X ′ S = \frac{1}{n - 1}XX^T = X'^TX' S=n−11XXT=X′TX′,其中 X ′ = 1 n − 1 X T X' = \frac{1}{\sqrt{n - 1}}X^T X′=n−11XT
容易看到 X ′ = U Σ V T X' = U\Sigma V^T X′=UΣVT中 V t V^t Vt的列向量记为单位特征向量
输入: m × n m\times n m×n样本矩阵X,其每一行元素的均值为0(以规范化),主成分个数k
输出: k × n k \times n k×n样本主成分矩阵Y
(1)工造新的 n × m n \times m n×m矩阵 X ′ = 1 n − 1 X T X' = \frac{1}{\sqrt{n - 1}}X^T X′=n−11XT
(2)对X’进行截断奇异值分解,得到 X ′ = U k Σ k V k T X' = U_k\Sigma_k V^T_k X′=UkΣkVkT
(3)样本主成分矩阵 Y = V T X Y = V^TX Y=VTX