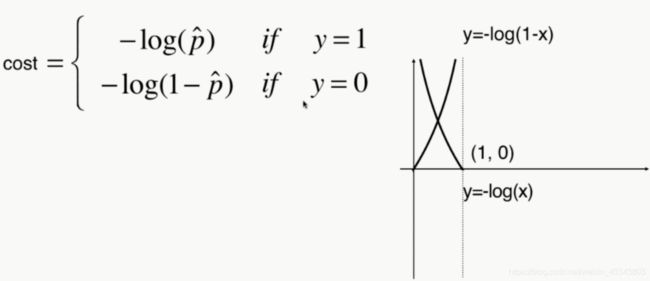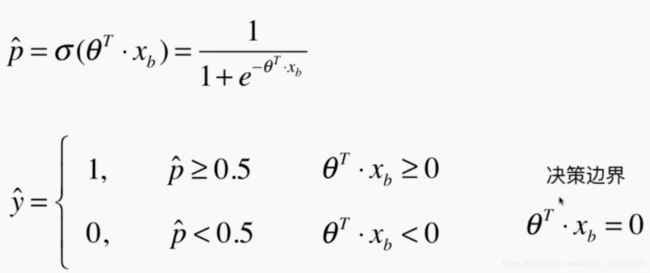机器学习——逻辑回归
14 逻辑回归
线性模型LR(没有考虑特征间的关联)——>LR +多项式模型(特征组合,不适用于特征稀疏场景,泛化能力弱)——>FM(适用于稀疏特征场景*,泛化能力强)——>FFM【省去零值特征,提高FFM模型训练和预测的速度,这也是稀疏样本采用FFM的显著优势】
14.1 what‘s Logistic Regression
逻辑回归是一种用于解决二分类问题的机器学习方法,用于估计某种事物的可能性。逻辑回归(LR,Logistic Regression)是传统机器学习中的一种分类模型,由于LR算法具有简单、高效、易于并行且在线学习(动态扩展)的特点,在工业界具有非常广泛的应用。
在线学习算法:LR属于一种在线学习算法,可以利用新的数据对各个特征的权重进行更新,而不需要重新利用历史数据训练。
LR适用于各项广义上的分类任务,例如:评论信息正负情感分析(二分类)、用户点击率(二分类)、用户违约信息预测(二分类)、用户等级分类(多分类 )等场景。
14.1.1 逻辑回归怎么解决分类问题
逻辑回归既可以看做是回归算法,也可以看做是分类算法。通常作为分类算法用,只可以解决二分类问题。
14.1.2 线性回归与逻辑回归的区别
线性回归模型既可以用于回归,也可以用于分类。
- 解决回归问题,可以用于连续目标值的预测。
- 但是针对分类问题,该方法则有点不适应,应为线性回归的输出值是不确定范围的,无法很好的一一对应到我们的若干分类中。即便是一个二分类,线性回归+阈值的方式,已经很难完成一个鲁棒性很好的分类器了。
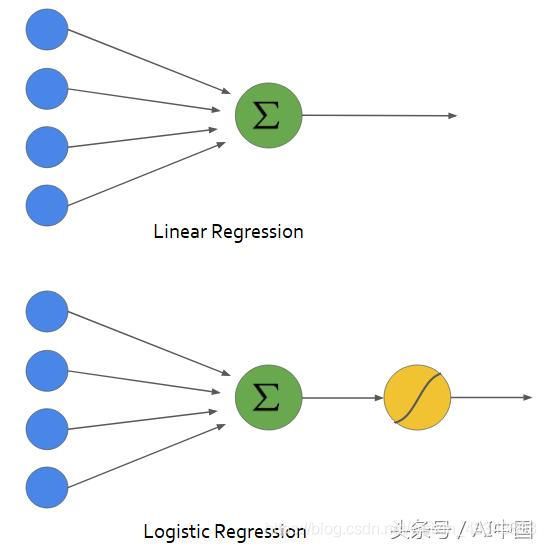
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。逻辑回归假设因变量 y 服从伯努利分布,属于参数模型,而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
从上面两张图可以看出,逻辑回归只是在线性回归的基础上添加了一个sigmoid函数,该函数可以将前面的结果映射到0~1之间的任何数值。
跟线性回归模型一样,逻辑回归模型也是计算输入特征的加权和(加上偏置项),但是不同于线性回归模型直接输出结果,它输出的是结果的数理逻辑。
14.1.3 Sigmoid函数
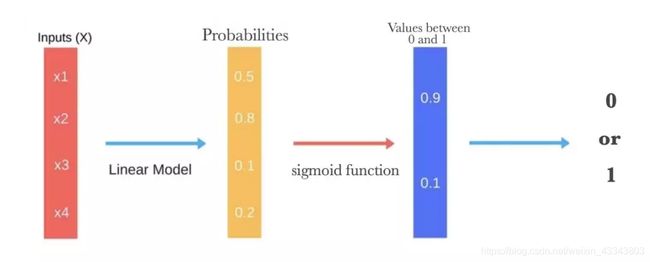
前面提到使用sigmoid函数,那么1)为什么需要使用sigmoid函数? 2)使用sigmoid函数怎么就可以将回归算法转变成分类算法?
1)为什么需要使用sigmoid函数?
我们可以回顾一下线性回归中的预测函数:
y ^ = f ( x ) \hat y=f(x) y^=f(x)
预测值 y ^ \hat y y^是一个连续值。
逻辑回归是用于估算一个实例属于某个特定类别的概率。我们在这里用 p ^ \hat p p^表示概率值。那么通过上面对比线性模型和逻辑模型,可以知道两种模型的前部分是一致的。故,有以下公式:
p ^ = f ( x ) \hat p=f(x) p^=f(x)
最后的输出预测我们依然使用 y ^ \hat y y^表示,在逻辑回归种,如果估算的概率超过50%,则模型预测为该实例属于该类别,反之,则预测不是。公式表示:
p ^ = f ( x ) \hat p=f(x) p^=f(x)
y ^ = { 1 , p ^ ≥ 0.5 0 , p ^ ≤ 0.5 \hat y=\begin{cases} {1},\hat p \geq 0.5\\ {0},\hat p \leq 0.5\end{cases} y^={1,p^≥0.50,p^≤0.5
这里很明显是对于计算出的概率进行判断,那么这样就可以进行分类操作,即分类算法。
继续回想一下线性回归中预测模型:
y ^ = f ( x ) → y ^ = θ T ⋅ x b 我 们 知 道 此 处 的 值 域 为 ( − ∞ , ∞ ) 概 率 的 值 域 为 [ 0 , 1 ] \hat y=f(x) \rightarrow \hat y=\theta^T\cdot x_b \\ 我们知道此处的值域为(-\infty,\infty)\\ 概率的值域为[0,1] y^=f(x)→y^=θT⋅xb我们知道此处的值域为(−∞,∞)概率的值域为[0,1]
因此,需要一个映射,将值域从无穷变换到0到1之间,即:
p ^ = σ ( θ T ⋅ x b ) \hat p=\sigma(\theta^T \cdot x_b) p^=σ(θT⋅xb)
这个映射就是Sigmoid函数。
σ ( t ) = 1 1 + e − t \sigma(t)=\frac {1}{1+e^{-t}} σ(t)=1+e−t1
如下图是Sigmoid函数的图像曲线:
所以,sigmoid函数的作用就是将值域从无穷变换到0-1之间的一个映射,成为一个概率预测问题。sigmoid函数也称逻辑函数,也许这就是逻辑回归名称的由来吧!(我猜的 ^__^ )
可以把LR看作单层的神经网络。
2)使用sigmoid函数怎么就可以将回归算法转变成分类算法?
由1)中可知逻辑回归的概率估算公式:
p ^ = σ ( θ T ⋅ x b ) = 1 1 + e − θ T ⋅ x b \hat p=\sigma(\theta^T\cdot x_b)=\frac{1}{1+e^{-\theta^T\cdot x_b}} p^=σ(θT⋅xb)=1+e−θT⋅xb1
逻辑回归模型预测:
y ^ = { 1 , p ^ ≥ 0.5 0 , p ^ ≤ 0.5 \hat y=\begin{cases} {1},\hat p \geq 0.5\\ {0},\hat p \leq 0.5\end{cases} y^={1,p^≥0.50,p^≤0.5
注意此时的分类是由 θ T ⋅ x b \theta^T \cdot x_b θT⋅xb决定的,如果 θ T ⋅ x b \theta^T \cdot x_b θT⋅xb是正类,逻辑回归模型预测结果是1,如果是负类,则预测为0。
自然,回归算法转变成分类算法就比较容易理解了。
14.2 训练和成本函数(目标函数)
现在你知道逻辑回归模型是如何估算概率并做出预测了。但是要怎么训练呢?训练的目的就是设置参数向量 θ \theta θ,使模型对正类实列做出高概率估算(y=1),对负类实例做出低概率估算(y=0)。
首先确定一下单个训练实例的成本函数(损失函数cost):
前面我们已经知道了逻辑回归模型的预测公式,也得到分类的标准是由 θ T ⋅ x b \theta^T \cdot x_b θT⋅xb决定的。如果实际值y分类为1,但是预测出的概率值p越小,则逻辑回归模型越有可能将其分类为0,这样我们模型预测的损失越大。反之亦然。
c o s t = { 如 果 y = 1 , p 越 小 , c o s t 越 大 如 果 y = 0 , p 越 大 , c o s t 越 大 cost=\begin{cases} 如果y=1,p越小,cost越大 \\ 如果y=0,p越大,cost越大\end{cases} cost={如果y=1,p越小,cost越大如果y=0,p越大,cost越大
我们需要将上面的文字逻辑转换为数学表达,这里借助log函数的特性:
将上面的分式用一个公式表示,即:这个公式也称为log损失函数。
c o s t = − y l o g ( p ^ ) − ( 1 − y ) l o g ( 1 − p ^ ) cost=-ylog(\hat p)-(1-y)log(1-\hat p) cost=−ylog(p^)−(1−y)log(1−p^)
整个训练集的成本函数即为所有训练实例的平均成本。
逻辑回归成本函数(log损失函数)(目标函数):
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( p ^ ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − p ^ ( i ) ) ] p ^ ( i ) = σ ( X b ( i ) θ ) = 1 1 + e − X b ( i ) θ J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}[y^{(i)}log(\hat p^{(i)})+(1-y^{(i)})log(1-\hat p^{(i)})] \\ \hat p^{(i)}=\sigma(X_b^{(i)}\theta)=\frac{1}{1+e^{-X_b^{(i)}\theta}} J(θ)=−m1i=1∑m[y(i)log(p^(i))+(1−y(i))log(1−p^(i))]p^(i)=σ(Xb(i)θ)=1+e−Xb(i)θ1
很遗憾,这个函数没有已知的闭式方程(不存在一个标准方程的等价方程)来计算出最小化成本函数的 θ \theta θ值。但是好消息是,这是个凸函数,所以可以通过梯度下降法保证能够找出全局最小值。下面给出成本函数关于第j个模型参数 θ j \theta_j θj的偏导数方程(及向量化):
∂ J ( θ ) ∂ θ j = − 1 m ∑ i = 1 m ( σ ( θ T ⋅ X ( i ) ) − y ( i ) ) x j ( i ) = 1 m X b T ( σ ( X b T θ ) − y ( i ) ) \frac {\partial J(\theta) } {\partial \theta_j }=-\frac{1}{m} \sum_{i=1}^{m}(\sigma(\theta^T\cdot X^{(i)})-y^{(i)})x_j^{(i)}\\ =\frac{1}{m}X_b^T(\sigma(X_b^ T\theta)-y^{(i)}) ∂θj∂J(θ)=−m1i=1∑m(σ(θT⋅X(i))−y(i))xj(i)=m1XbT(σ(XbTθ)−y(i))
14.3 决策边界
模型估算概率为50%的点,即模型的决策边界。
#### 14.4 模型优化—引入正则化 与其他线性模型一样,当模型的参数过多时,很容易遇到过拟合的问题。这时就需要有一种方法来控制模型的复杂度,典型的做法在优化目标中加入正则项,通过惩罚过大的参数来防止过拟合。逻辑回归模型可以用L1或L2惩罚函数来正则化。但是逻辑回归模型中的超参数不是 α \alpha α,而是它的逆反:C,C的值越高,模型的正则化程度越高。
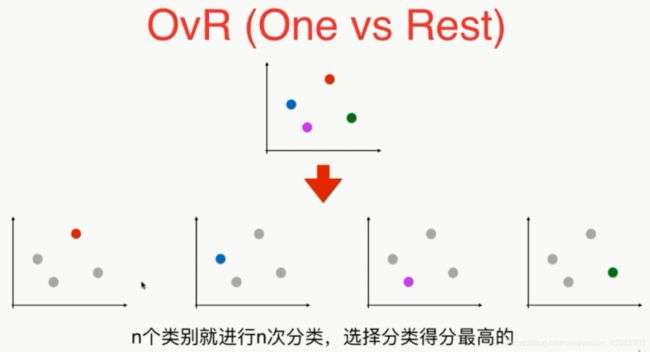
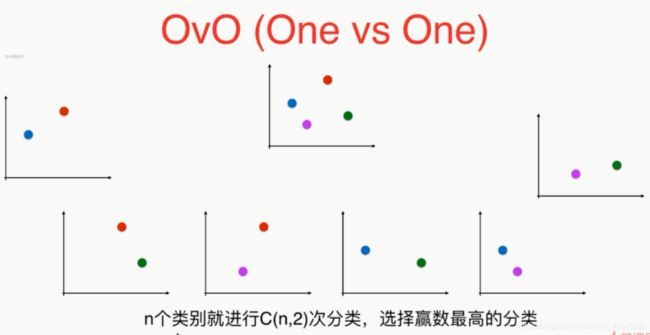
14.5 多分类问题
逻辑回归模型是一个解决二分类的算法,不过也可以用于解决多分类问题:
OvR 和 OvO