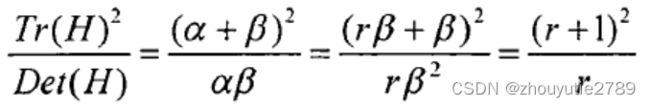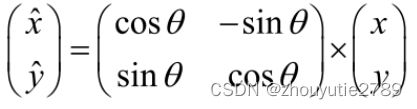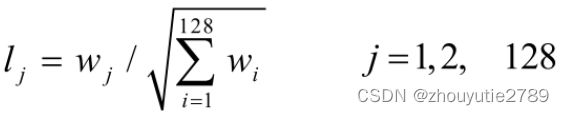尺度不变特征变换（SIFT）特征点检测

一、SIFT算法

1、建立高斯差分尺度空间

由于高斯核是唯一可以产生尺度空间的核，一个图像的尺度空间,定义为原始图像与一个尺度可变的高斯函数的卷积。

二维高斯函数定义：

 表示像素点坐标，表示图像数据，表示尺度因子（高斯正态分布方差），表示高斯尺度空间

——————————————————————————————————————————

 注：其中存在高斯模糊这个概念，通常用于减小图像噪声以及降低细节层次

——————————————————————————————————————————

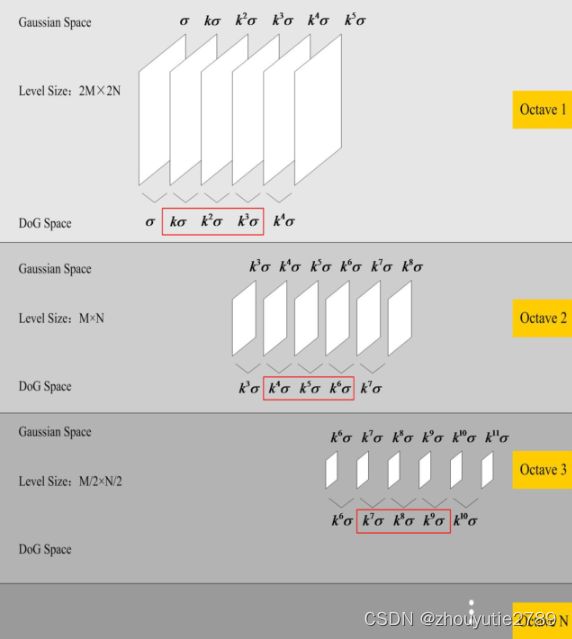
构造图像金字塔

可将高斯金字塔组内和组间尺度归纳为：

 i表示金字塔组数，n表示当前组的层数，S表示当前组的层的总数（一半为3~5）

根据下式确定高斯金字塔的组数

 M，N表示图像的行数和列数

高斯差分算子定义：

 

 因此得到高斯差分尺度空间，过程如下图：

2、局部极值点检测

为检测出图像高斯差分尺度空间的极值，图像每个像素与其余26个像素进行比较，仅当被检测点为极大（小）值时，保存并进行后续计算。

利用DOG函数在尺度空间的泰勒展开式：

 其极值点为

 并在计算中对行、列、尺度三个量进行修正，得到：

 将修正结果代入DOG函数在尺度空间上的泰勒展开式：

 该式能去除那些对比度较低的不稳定的极值点

———————————————————————————————————————————

注意：在极值比较中，每一组的首末两层无法进行极值比较，为满足尺度变化的连续性，在每一组图像的顶层继续用高斯模糊生成了三幅图像，因此高斯金字塔每组有S+3层，DOG金字塔每组有S+2层。下图为不同尺度不同层间极值检测图

———————————————————————————————————————————

3、边缘点剔除

注意：这里我们是提取点，而高斯差分函数在图像的边缘产生较强响应，应剔除边缘点保证算法稳定性和抗噪能力

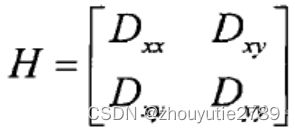
利用Hessian矩阵消除图像边缘点，Hessian矩阵定义如下：

 利用矩阵的行列式和迹，求解出Hessian矩阵的特征值（与Harris角点检测相似）。

其中 ，当r接近1时表示两个主曲率比较接近，此时可判定该点为一个特征点。为判定r，采用下式：

通常，r<10 判定该点为特征点，r>10的像素点大多是图像边缘像素自动剔除。也就是说只需要判断

 

 上式小于12.1就行

通过尺度不变性求得极值点，可以使描述子具有缩放不变性

4、关键点方向分配

原理：利用关键点邻域像素的梯度方向分布特性，为每个极值点赋予方向，从而使描述子具有旋转不变性

像素点的梯度表示

 梯度幅值：

梯度方向：

 

 为确定极值点方向采用梯度直方图统计法，统计以极值点为原点，一定区域内的图像像素点对关键点方向生成所做贡献

——————————————————————————————————————————

梯度直方图

1、直方图以每10度方向为一个柱，共36个，柱代表的方向为像素点的梯度方向，柱的长短代表梯度幅值

2、直方图统计半径为3*1.5*

3、在直方图统计时，每相邻三个像素点采用高斯加权，模板选用[0.25,0.25,0.25]，并连续加权两次

4、极值点主方向：极值点周围区域梯度直方图的主峰值就是特征点方向

      极值点辅方向：在梯度直方图中，存在另一个相当于主峰值80%能量的峰值时，该方向为极值点的辅方向

      这能增强匹配的鲁棒性

——————————————————————————————————————————

方向分配实现步骤：

 综上，图像的关键点检测完成，每个关键点有三个信息：位置、尺度、方向；同时这些关键点也拥有了平移、缩放和旋转的不变性。

5、关键点描述

关键点进行描述的原因：该描述子不仅包括关键点，也包括关键点周围对其有贡献的像素点。描述子作为目标匹配的依据，也可使关键点具有更多的特性，比如光照不变性，3D视点变化等。

描述思路：对关键点周围图像分区，计算块内梯度直方图，生成具有独特性的向量（唯一性）

下图为描述子事例，

假设描述子由2*2*8维向量（也就是2*2个8方向直方图）表示，箭头方向代表像素的梯度方向，箭头的长度代表该像素的幅值大小。

 经过作者实验得出，描述子采用4*4*8=128维向量表征，效果最好

128维描述子生成步骤：

1、确定计算描述子所需图像区域

描述子区域的半径由下式计算得出：

 其中d=4,为关键点所在组的尺度

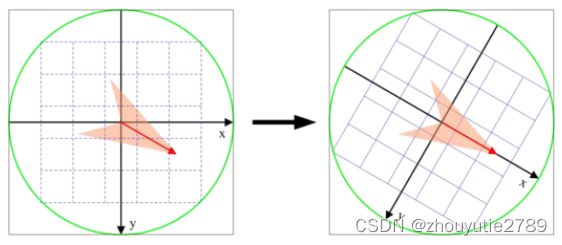
2、将坐标移至关键点主方向

旋转后的新坐标：

 3、在图像半径内对每个像素点求其梯度幅值和方向，然后对每个梯度幅值乘以高斯权重参数，形成梯度直方图

 其中表示该像素点与关键点的列距离，表示该像素点与关键点的行距离，等于描述子窗口宽度（3）乘以直方图列数的一半（2）？

 4、在窗口宽度为2*2区域内计算8个方向的梯度直方图，绘制每个梯度方向的累加值，就能形成一个种子点。然后再在下一个2*2区域内进行直方图统计，形成下一个种子点。（由于我们这里描述子采用4*4*8）共生成16个种子点

5、描述子向量元素门限化及门限化后描述子向量规范化

描述子向量元素门限化：方向直方图每个方向上梯度幅值限制在一定门限值（0.2）以下

描述子向量元素规范化：得到的128个描述子向量：

                                        规范化后的向量：

                                        规范化公式：

                                                                 

                                        关键点描述子向量的规范化正是可以去除光照影响，也能解决图像灰度                                            值整体漂移的问题

 6、关键点匹配

分别对参考图像和待配准图像建立描述子集合，通过对比点集内关键点的描述子完成匹配。相似性度量方法采用欧式距离。

这里threshhold代码里取的是0.9

匹配方法1：穷举匹配（耗费时间较长，不采用）

匹配方法2：Kd树

7、消除错误配准点

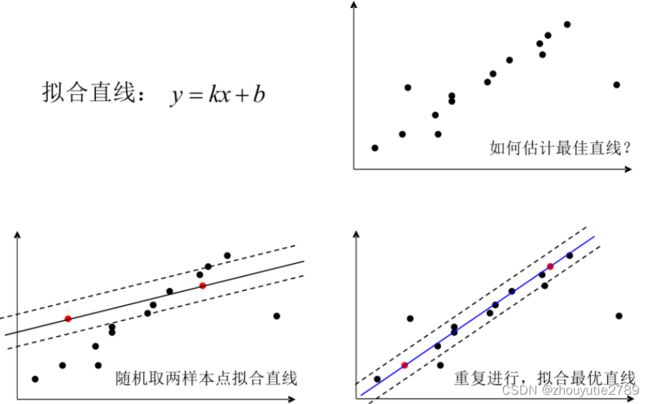
RANSAC（Random Sample Consensus，随机抽样一致）：根据具体问题设计得到某个目标函数，然后通过反复提取最小点集估计该函数中参数的初始值，利用初始值把所有的数据分为内点和外点，最后用所有的内点重新计算和估计函数的参数

RANSAC实例：

SIFT实现步骤（根据代码）

（1）读入待配准图像、参考图像

（2）将待配准图像和参考图像转换为灰度图像，同时将途中像素点的数据类型转换成浮点型数据

（3）定义一些常用的常量，比如sigma(底层图像尺度)、对比度阈值、边缘阈值等

（4）构建参考图高斯金字塔，返回gaussian_pyramid_1（各个尺度的高斯图像，采用高斯模糊实现），gaussian_gradient_1（高斯图像金字塔梯度）,gaussian_angle_1（高斯金字塔的方向）。他们的size都是7*6（7层6组）

（5）构造参考图DOG金字塔，得到dog_pyramid_1（大小为7*5）

（6）对参考图进行极值点检测，剔除图像边界点，筛选出区域内极大/小值点；计算出前一步所得极值点的偏移量；剔除偏差大的极值点；剔除不稳定的极值点；剔除不在该层该层图像区域内的极值点（x、y、）；剔除边缘点。同时为得到极值点方向，用梯度直方图calculate_oritation_hist，得到key_point_array_1（x、y、Octaves、layer、xi、size、angle、gradient）

（7）对参考图生成描述子，可采用DOG或GLOH或GLOJH-like.以DOG为例，每个极值点采用4*4*8维描述子描述。首先确定描述子区域；将坐标转换为关键点主方向；图像半径内对每个像素点求其梯度幅值和方向，然后对每个梯度幅值乘以高斯权重参数，形成梯度直方图；在窗口宽度为4*4区域内计算8个方向的梯度直方图，绘制每个梯度方向的累加值，就能形成一个种子点；再描述子规范化及门限化。得到参考图关键点描述子descriptors_1和locs_1（y、x、size、angle、gradient、Octaves、layer）

（8）对待配准图像重复上述（4）-（7）步骤

（9）配准。采用欧式距离的方法进行相似性度量，当最近邻距离/次近邻距离<0.9时，判定为匹配点；采用unique进行对比，删除重复点对；

*确定匹配点后，必须对参考图像和待配准图像之间的最佳模型参数进行求解

重复迭代求解出模型参数后，得到solution（大小为3*3矩阵），rmse（均方根误差）、cor1（参考图像关键点信息，包括x,y,组，层，尺度，角度）、cor2（待配准图关键点信息）

（10）图像融合。首先定义融合图像，大小为（3*M，3*N，3）；采用makeform创建待配准图的投影变换结构 tform，并据二维空间变换结构tform对待配准图像image_1进行二维空间变换；对image_2也同理,得到fusion_image；最后删除多余区域，得到最后融合图像。

 二、SIFT应用领域

物体识别

机器人定位及导航

图像拼接

三维建模

手势识别

视频跟踪

笔迹鉴定

指纹及人脸识别

三、SIFT算法的改进

PCA-SIFT：通过PCA降维，有效化简SIFT的128维描述子

CSIFT：彩色尺度特征不变变换，可针对彩色图像进行图像的不变特征提取

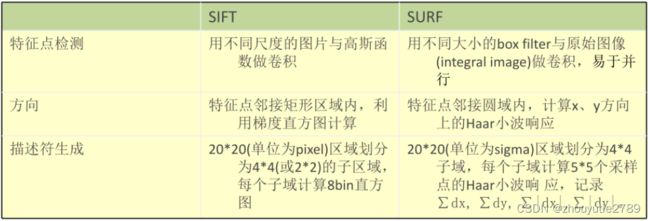
SURF：

ASIFT：抗仿射SIFT变换，两个向量空间之间的一个仿射变换（放射映射）由一个线性变换+一个平移组成，该方法能抵抗强仿射情况，且提取的特征点远多于SIFT算法