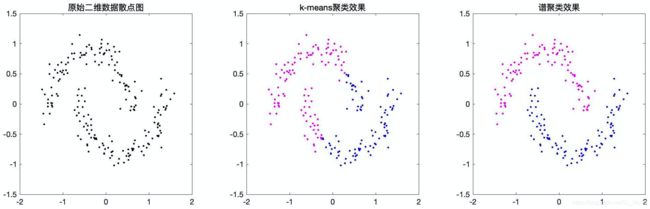
带你玩转谱聚类及拉普拉斯矩阵

引言：在多变量统计和数据聚类中，谱聚类(Spectral Clustering)技术利用数据的相似矩阵的谱(特征值)进行降维。它将数据看成空间中的点，点对之间有边相连，距离越远的点对其边权值越小，距离越近的点对其边权值越大。它将聚类问题转化为切图问题，使得切图后的总代价最小。即子图内点对之间边权值较大，子图间边权值较小。得到切图后子图的个数即为聚类的个数。最后本文力求用推理而非演绎的方式以加深大家对谱聚类的理解。

申明：本文严禁转载！

带着问题去阅读：

1. 为什么叫谱聚类？谱的含义是什么？(见引言，矩阵的谱表示其特征值的集合)
2. 谱聚类如何将聚类问题转化为图切割问题，常用的图构造方法是什么？
3. 为什么要引入Laplacian矩阵？它有哪些性质？
4. 为什么要取Laplacian矩阵第$\text{2}$小或前$k$小个特征值对应的特征向量？其特征值$\lambda$有什么意义？它和瑞利商$\text{(Rayleigh Quotient)}$有什么关系？前$k$小中的$k$一定和聚类个数$c$相等吗？
5. 为什么Laplacian矩阵0特征值的数量就是连通子图的个数？
6. 谱聚类如何将一个难求解的离散优化问题松弛为易求解的连续优化问题？
7. 为什么最后还要对特征向量进行k-means聚类？(需要将连续值离散化)
8. 原目标函数聚类效果已经不错，为什么还要对拉普拉斯矩阵$L$进行归一化，有几种归一化方法？分别又是什么？($L_{rw}$和$L_{sym}$)
9. 对于三种图拉普拉斯矩阵$L,L_{rw}$和$L_{sym}$，它们的适用场景是什么？
10. 我们发现在吴恩达($\text{Ng}$)等人提出的算法中，在构造了$L_{sym}$归一化矩阵后，又对前$k$个特征向量构成的矩阵$U\in R^{n\times k}$按行再次进行了归一化，这样做是否多此一举？$\text{Ng}$等人的目的何在？
11. 通过对谱聚类的学习，有哪些我们可以借鉴的思想可以用于我们的科研工作当中？

一、问题抽象

假设有$n$个实数样本数据如下，每个样本有$d$维，目标是要聚$c$个类，并且数据分布并非云团，如何做？

$$X=\{x_1^d,x_2^d,...,x_n^d{\}}^T，X\in R^{n\times d}$$

将数据点抽象为无向带权图(图构造)

在图论中我们常用邻接矩阵W表示图(无向图是为了保证邻接矩阵是对称矩阵)，因此我们只需按某个准则来计算数据点对之间的距离即可获得数据点的邻接矩阵。因此引出以下常用$3$种准则来构造图。(对于3个数据点的邻接矩阵如下)
$$\begin{array}{c}W=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]\end{array}$$

1.1 全连接法

所有点对之间的边权值均为正数(＞0)，采用核函数作为准则来计算点对之间的距离(也称为相似度或亲和度)，进而直接得到实对称相似度矩阵$W=W^T$，常用高斯核函数。令$s_{ij}$表示两点之间的边权重(也称两点相似度)，则高斯核计算公式如下
$$w_{ij}=s_{ij}=s(x_i,x_j)=e^{-\frac{||x_i-x_j|{|}_2^2}{2{\sigma }^2}}\text{\hspace{1em}(1.1)}$$
其中参数$\sigma$控制着点对$x_i$与$x_j$之间的度量，$\sigma$越大，两点度量后的差距越小，聚类精度也越低；$\sigma$越小，两点度量后的差距越大。

1.2 $k$-近邻法

计算点对之间的欧氏距离，通过给定参数$k$，选取距离当前点最近的$k$个点为邻居(常用高斯核计算距离)，令其余点到该点距离为0。
$$w_{ij}=\{\begin{array}{ll}{e}^{-\frac{||x_i-x_j|{|}_2^2}{2{\sigma }^2}}& if{x}_i\in knn(x_j)\\ 0& otherwise\end{array}(可能存在w_{ij}\ne w_{ji})\text{\hspace{1em}(1.2)}$$

然而，这样做有一个显著的问题，数据从无向图变成了有向图。即你是我的邻居，但我不一定是你的邻居(即$w_{ij}\ne w_{ji}$)。为了保证相似度矩阵的对称性，论文[1]给出了两种解决方法将有向图变成无向图。

• 方法一：若两点间有两条有向边，则忽视一条，仅保留一条。具体做法如下：
  $$w_{ij}=w_{ji}=\{\begin{array}{ll}{e}^{-\frac{||x_i-x_j|{|}_2^2}{2{\sigma }^2}}& if{x}_i\in knn(x_j)or{x}_j\in knn(x_i)\\ 0& otherwise\end{array}\text{\hspace{1em}(1.3)}$$

• 方法二：当且仅当你是我的邻居，并且我也是你的邻居时，我俩之间才有边权值。具体做法如下
  $$w_{ij}=w_{ji}=\{\begin{array}{ll}{e}^{-\frac{||x_i-x_j|{|}_2^2}{2{\sigma }^2}}& if{x}_i\in knn(x_j)and{x}_j\in knn(x_i)\\ 0& otherwise\end{array}\text{\hspace{1em}(1.4)}$$

• 方法三：采用平均化思想，先求每个点的$k$近邻，得到不对称的有向图。然后采用如下做法变成对称的无向图，这也是实战常用的方法之一：

$$W=\frac{W+W^T}{2}\text{\hspace{1em}(1.5)}$$

1.3 $ϵ$-近邻法

给定一个阈值$ϵ$，如果两点距离大于这个阈值则认为这两点无边相连，否则这两点间的边权值为$ϵ$。具体做法如下：
$$w_{ij}=w_{ji}=\{\begin{array}{ll}ϵ& ifs(x_i,x_j)<ϵ\\ 0& otherwise\end{array}\text{\hspace{1em}(1.6)}$$
该方法得到的矩阵可视为无向无权图，因此精度不如其他方法。

二、目标函数的转化

经过问题抽象后，我们将原始数据按k近邻法构造出如下拓扑图。现在我们可以将聚$c$个类的问题转化为将无向图切割为$c$个子图的问题。

由上图可知，切分的方法有很多，我们该如何切出$c$个子图从而达到我们想要聚类的效果呢？很容易想到一个准则，即不同切图方法需要付出不同的代价，当我们将距离较近的看似为同一个类的两个点切分为不同类时，需要付出较大代价；当我们将距离较远的两个点切分到不同子图时，需要付出较小代价。因此我们可以定义一个代价函数来作为我们初步的目标函数。

2.1 初始目标函数的形成(最小割$\text{Min Cut}$方法)

我们令无向图$G=<V,E>$，其中$V\in R^{n\times d}$是$n$个$d$维顶点的集合，$v_i$表示第$i$个顶点。$E$是边的集合，$e_{ij}$表示顶点$v_i$到点$v_j$的边。假设我们要将所有顶点$V$切分成$c$个子图，则令$A_i$表示第$i$个子图所包含顶点的集合(称为图$G$的一个分割)，${\overline{A}}_i$表示第$i$个子图的补图(其中$i=1,2,...,c$，所以$V=A_1\cup A_2\cup ...\cup A_c$)。现在我们令$Cut(V)$来表示切图的代价，则

$$Cut(V)=Cut(A_1,A_2,...,A_c)\text{\hspace{1em}(2.1)}$$
这是一个典型的$one\text{vs}all$问题，由于我们不知道$A_i$中都有哪些顶点，大的分类问题我们不会做，我们可以先找最简单的$case$(即二分类)来做，然后再将多个小问题的解合并为一个大问题的完整解，显然该问题是可分且子问题的解也可合并，所以利用分治思想我们可将一个多分类问题转化为多个二分类问题。

方便起见，我们用$W(A_i,{\overline{A}}_i)$来表示子图$A_i$和其补图${\overline{A}}_i$被切割后的代价，而二分类中两个子图的分割代价可用连接两个子图的所有边的权值之和来表示(前面提到边权值越大两点越近，反之越远)。因此进一步得到如下式子(左乘$1/2$是因为对称性$w_{ij}=w_{ji}$，相当于算了两遍)：
$$Cut(V)=Cut(A_1,A_2,...,A_c)=\sum _{k=1}^{c}Cut(A_k,{\overline{A}}_k)=\frac{1}{2}\sum _{k=1}^{c}W(A_k,{\overline{A}}_k)=\frac{1}{2}\sum _{v_i\in A_k,v_j\in {\overline{A}}_k,e_{ij}\in E}{w}_{ij}(i,j=1,2,...,n)\text{\hspace{1em}(2.2)}$$
因此，我们可以进一步得到初步离散优化问题，即最小割目标函数：
$$\min Cut(V)\Rightarrow \min \sum _{v_i\in A_k,v_j\in {\overline{A}}_k,e_{ij}\in E}{w}_{ij}\text{\hspace{1em}(2.3)}$$

2.2 细化初始目标函数之引入指示向量($\text{indicator vector}$)

得到最小割目标函数后，我们发现其约束$v_i\in A_k,v_j\in {\overline{A}}_k,e_{ij}\in E$过于笼统模糊，难以求解。因此，我们需要定性地引入指示向量来细化目标函数。在此我们先避开聚多类问题，从最简单的二聚类问题开始讨论，再逐步归纳到多聚类问题。

2.2.1 先讨论二聚类问题($c=2$)

对于聚二类问题，我们不再需要$A_i$，仅用$A$足以表示$G$的一个分割，另一个分割用$\overline{A}$表示。因此原目标函数为
$$\min Cut(V)\Rightarrow \min Cut(A,\overline{A})\Rightarrow \min \sum _{v_i\in A,v_j\in \overline{A},e_{ij}\in E}{w}_{ij}\text{\hspace{1em}(2.4)}$$

① 目标函数的展开

对目标函数观察后我们发现，第三个约束$e_{ij}\in E$很好处理，如在构图方法中选择$k$近邻法，使得点对之间有边相连时$w_{ij}>0$，无边相连时$w_{ij}=0$，因此选择$k$近邻法可直接去除该约束。

对于剩下的两个约束$v_i\in A,v_j\in \overline{A}$，我们定义指示向量$f=(f_1,f_2,...,f_n{)}^T\in N^n$(注：此处的$f_i$是一个布尔值而不是向量)并满足如下条件：
$$f_i=\{\begin{array}{ll}1& if{v}_i\in A\\ 0& if{v}_i\in \overline{A}\end{array}\text{\hspace{1em}(2.5)}$$
这样的指示向量在论文[1]中被称为理想型指示向量(ideal indicator vector)。假设每个样本点以概率为$1$属于某个类，不存在某个样本属于多个类的情况。我们的目的是，当满足约束$v_i\in A,v_j\in \overline{A}$时$w_{ij}$有值，否则不对其进行求和。因此可以借助指示向量将目标函数细化如下：
$$\min Cut(A,\overline{A})\iff \min \frac{1}{2}\sum _{v_i\in A,v_j\in \overline{A},e_{ij}\in E}{w}_{ij}\iff \min \frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2$$
现在先不着急求解目标函数，我们展开$w_{ij}(f_i-f_j{)}^2$二次项如下：
$$\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n(w_{ij}{f}_i^2-2f_i{f}_j{w}_{ij}+w_{ij}{f}_j^2)\text{\hspace{1em}(2.6)}$$

② 非标准化$\text{Laplacian}$矩阵的引入

已知在图论中，一个无向图$G$中第$i$个顶点的(degree)度$d_i$表示如下：
$$d_i=\sum _{j=1}^n{w}_{ij}\text{\hspace{1em}(2.7)}$$
因此上式可以继续展开如下，看到加权求和我们可以快速想到两向量的点积：
$$\begin{array}{rl}\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2& =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n(w_{ij}{f}_i^2-2f_i{f}_j{w}_{ij}+w_{ij}{f}_j^2)\\ & =\frac{1}{2}(\sum _{i=1}^n{d}_i{f}_i^2-\sum _{i,j=1}^{n}2f_i{f}_j{w}_{ij}+\sum _{j=1}^n{d}_j{f}_j^2)\\ & =\frac{1}{2}(2\sum _{i=1}^n{d}_i{f}_i^2-2\sum _{i,j=1}^n{f}_i{f}_j{w}_{ij})\\ & =\sum _{i=1}^n{d}_i{f}_i^2-\sum _{i,j=1}^n{f}_i{f}_j{w}_{ij}=\sum _{i=1}^n{f}_i{d}_i{f}_i-\sum _{i,j=1}^n{f}_i{w}_{ij}{f}_j\\ & =f^{T}Df-f^{T}Wf\\ & =f^{T}Lf\end{array}\text{\hspace{1em}(2.8)}$$
其中，$D$为度矩阵，$W$为邻接矩阵(相似矩阵)，而$L=D-W$为Laplacian矩阵。没想到从一个二次项$w_{ij}(f_i-f_j{)}^2$目标函数经过展开可以得到拉普拉斯矩阵。因此，原目标函数再次等价于：
$$\begin{array}{rlr}\underset{A\subset V}{\mathrm{argmin}}Cut(V)\iff & \underset{f_i\in N^n}{\mathrm{argmin}}\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2\iff & \underset{f_i\in N^n}{\mathrm{argmin}}{f}^{T}Lf\\ & s.t{f}_i\text{as defined in Eq. (2.5)}& \end{array}$$
现在，我们通过引入布尔指示向量将一个抽象的切割函数$Cut(V)$转化为具体可求解的$f^{T}Lf$。但是我们通过约束$(2.5)$发现这是一个离散优化函数，无法对其求导。

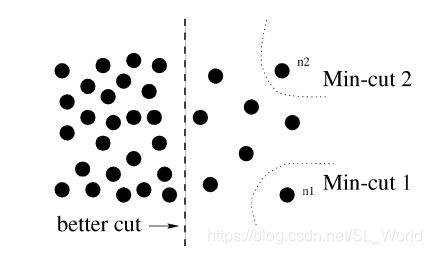
不过，最小割问题已经有确定解法，只是这不是我们在此讨论的重点，最小割目标函数在谱聚类问题中的定义本身存在偏离，其分割结果往往更倾向于将所连边最少且边权值较低的孤立点分割出来。因此需要继续改进，具体如何改进我们将在2.3章节详细讨论。我们在此之所以对最小割目标函数的转换讨论这么详细是因为这个思想在后面会用到。

2.2.2 再回到多聚类问题($c$取任意值)

讨论完二聚类的简单问题，我们再来归纳到多聚类问题就容易多了。对于多聚类问题，我们要聚$c$个类($k=1,2,...,c$)，因此我们仅仅需要将原来一个指示向量扩展为$c$个指示向量组合成的指示矩阵$H$即可，其余步骤相似。

指示向量扩展到指示矩阵

对于多聚类问题，我们依然定义指示向量，只需要最后把$c$个指示向量组合成一个指示矩阵即可。

我们定义指示向量$h_k=(h_{(1,k)},h_{(2,k)},...,h_{(n,k)}{)}^T\in N^{n\times 1}$(其中：$k=1,2,...,c$)并满足如下条件：
$$h_{ik}=\{\begin{array}{ll}1& if{v}_i\in A_k\\ 0& otherwise\end{array}(i=1,...,n;k=1,...,c)\text{\hspace{1em}(2.9)}$$
现在，我们将这$c$个指示向量$h_k$组合成一个指示矩阵$H\in N^{n\times c}$，由于我们假设每个样本以概率为1属于某个类，因此矩阵$H$当中的每一列指示向量正交(orthonormal)于其他任何一列向量。(注意：向量之间的正交不代表$H$是正交阵)
【例如】我们要聚$c=3$个类，有$5$个样本，聚类得到的情况是前两个样本属于一个类，接着两个样本属于一个类，最后一个样本独成一类。则
$$\begin{array}{c}{H}^{T}H=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 1\end{array}\right]\end{array}$$
用数学语言可表达为：$\text{Tr}(H^{T}H)=n>0$。因此我们可以得到如下目标函数
$$\begin{array}{rl}\underset{A_1,...,A_c}{\mathrm{argmin}}Cut(A_1,...,A_c)\iff \underset{H\in R^{n\times c}}{\mathrm{argmin}}& \text{Tr}(H^{T}LH)\\ s.t& \text{Tr}(H^{T}H)=n\\ & H\text{ as defined in Eq.}(2.9)\end{array}$$

最终，我们按照二聚类的思路，结合扩展的指示矩阵可以得到相似的最小割目标函数。但是由于最小割目标函数的局限性。下面，我们将对最小割目标函数进行改进，并重新定义指示向量的值。

2.3 目标函数的改进($\text{RatioCut}$与$\text{Ncut}$)

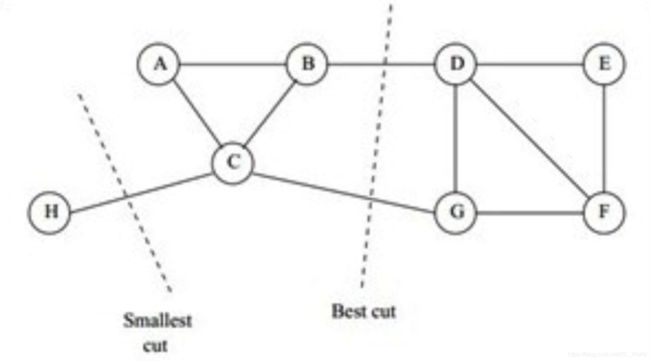
由最小割目标函数可知，最小割得到的分割结果往往更倾向于将所连边最少且边权值较低的孤立点分割出来。如下图所示，我们更希望被分割的子图中顶点的数量相互均衡。因此我们需要加入其它限制以改进目标函数分割效果。

为了达到均衡的效果，我们很容易想到在原目标函数(切成每个子图的代价)的基础上除以切图后每个子图的规模。

因此，现在的问题就是如何度量切图后子图的规模? ①从顶点数的角度思考可以想到用子图的顶点数作为该子图的规模。②从边的角度思考可以想到用子图的边权和作为子图的规模。两种度量方式用数学语言有如下定义：
$$\begin{array}{rl}& 子图A的势|A|:=\text{the number of vertices in }A\\ & 子图A的体积vol(A):=\sum _{v_i\in A}{d}_i\end{array}\text{\hspace{1em}(2.10)}$$
可以看出第二种子图A的体积更能贴切描述子图的规模，因为它相比子图A的势含有边权值的信息，能更清楚的区别有相同顶点数的但边权和不同的规模。当原二聚类目标函数为
$$Cut(V):=Cut(A_1,A_2,...,A_c)=\sum _{k=1}^{c}Cut(A_k,{\overline{A}}_k)=\frac{1}{2}\sum _{k=1}^{c}W(A_k,{\overline{A}}_k)$$
根据前面规模的定义式$(2.10)$，我们可以得到如下两个改进后的目标函数$RatioCut$(比例切割)与$Ncut$(归一化切割)：
$$\begin{array}{rl}& RatioCut(A_1,A_2,...,A_c):=\sum _{k=1}^c\frac{Cut(A_k,{\overline{A}}_k)}{|A_k|}=\frac{1}{2}\sum _{k=1}^c\frac{W(A_k,{\overline{A}}_k)}{|A_k|}\\ & Ncut(A_1,A_2,...,A_c):=\sum _{k=1}^c\frac{Cut(A_k,{\overline{A}}_k)}{vol(A_k)}=\frac{1}{2}\sum _{k=1}^c\frac{W(A_k,{\overline{A}}_k)}{vol(A_k)}\end{array}\text{\hspace{1em}(2.11)}$$
得到改进后的目标函数后，我们将尝试对其进行求解。

三、目标函数的求解

下面，我们先从非标准化$RatioCut$目标函数讲起。

3.1 $\text{RatioCut}$目标函数的近似解

3.1.1 先从二聚类说起($c=2$)

我们要求解的二聚类目标函数为
$$\underset{A\subset V}{\min }RatioCut(A,\overline{A})$$
现在，我们重新定义一下在$RatioCut$目标函数中的指示向量为$f=(f_1,f_2,...,f_n{)}^T\in R^n$

$$f_i=\{\begin{array}{ll}\sqrt{\frac{|\overline{A}|}{|A|}}& if{v}_i\in A\\ -\sqrt{\frac{|A|}{|\overline{A}|}}& if{v}_i\in \overline{A}\end{array}\text{\hspace{1em}(3.1)}$$
在之前，我们推导出
$$\min Cut(V)\iff \min f^{T}Lf$$
现在我们来反向推导一下看看能得出什么
$$\begin{array}{rl}{f}^{T}Lf& =\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2\\ & =\frac{1}{2}\sum _{v_i\in A,v_j\in \overline{A}}{w}_{ij}(\sqrt{\frac{|\overline{A}|}{|A|}}+\sqrt{\frac{|A|}{|\overline{A}|}}{)}^2+\frac{1}{2}\sum _{v_i\in \overline{A},v_j\in A}{w}_{ij}(-\sqrt{\frac{|A|}{|\overline{A}|}}-\sqrt{\frac{|\overline{A}|}{|A|}}{)}^2\\ & =cut(A,\overline{A})(\frac{|\overline{A}|}{|A|}+\frac{|A|}{|\overline{A}|}+2)\\ & =cut(A,\overline{A})(\frac{|\overline{A}|+|A|}{|A|}+\frac{|A|+|\overline{A}|}{|\overline{A}|})\\ & =|V|\cdot cut(A,\overline{A})(\frac{1}{|A|}+\frac{1}{|\overline{A}|})\\ & =|V|\cdot RatioCut(A,\overline{A})\end{array}\text{\hspace{1em}(3.2)}$$

我们得到了$RatioCut$目标函数！！同时对于指示向量的正交性，我们有$f\perp 1$，证明如下
$$\sum _{i=1}^n{f}_i\cdot 1=\sum _{v_i\in A}\sqrt{\frac{|\overline{A}|}{|A|}}-\sum _{v_i\in \overline{A}}\sqrt{\frac{|A|}{|\overline{A}|}}=|A|\sqrt{\frac{|\overline{A}|}{|A|}}-|\overline{A}|\sqrt{\frac{|A|}{|\overline{A}|}}=0$$
同时我们还发现$f^{T}f$内积可得到一个常数。
$$f^{T}f=\sum _{i=1}^n{f}_i\cdot f_i=\sum _{v_i\in A}\frac{|\overline{A}|}{|A|}+\sum _{v_i\in \overline{A}}\frac{|A|}{|\overline{A}|}=|A|\frac{|\overline{A}|}{|A|}+|\overline{A}|\frac{|A|}{|\overline{A}|}=|V|=n\text{\hspace{1em}(3.3)}$$

这是非常关键的条件！我们用拉格朗日乘子转化为无约束问题后可以得到一个有趣的结论。现在我们可以得到等价的完整目标函数
$$\begin{array}{rl}\underset{A\subset V}{\min }RatioCut(A,\overline{A})\iff & \underset{f\in R^n}{\min }{f}^{T}Lf\\ & s.tf\perp 1\\ & f_i\text{ as defined in Eq.(3.1)}\\ & f^{T}f=n(f^{T}f>0)\end{array}$$
在《A tutorial on spectral clustering》[1]这篇论文中(如下图)，作者将第三个约束条件写为$||f||=\sqrt{n}$，即$f^{T}f$得到的是一个常数。也是一个等式约束，即$f^{T}f-n=0$。

由于约束$f_i\text{ as defined in Eq.(3.1)}$的限制，即解向量$f_i$的取值只有两个值，导致该问题是一个NP难的离散优化问题，目标函数不可导。

如何解这个离散问题？

离散问题我们很难做或者不会做，但连续问题我们会做，所以我们想可不可以把离散问题转化成连续问题？在这里，我们可以放松一下约束条件，去掉$f_i\text{ as defined in Eq.(3.1)}$这个令人头疼的限制，使得解向量$f_i$可取实数域$R$中的任意值。这样就将离散问题松弛为连续问题如下
$$\begin{array}{rl}& \underset{f\in R^n}{\min }{f}^{T}Lf\\ & s.tf\perp 1(\text{that is }{f}^{T}1=0)\\ & f^{T}f=n(f^{T}f>0)\end{array}\text{\hspace{1em}(3.4)}$$

使用拉格朗日乘子将约束问题转化为无约束问题

有约束的目标函数我们不会做，我们可以转化为无约束问题，因此目标函数$(3.4)$可以转化为如下$Lagrange$函数$L(f,\lambda )$
$$\begin{array}{rl}L(f,\lambda ):& =f^{T}Lf-\lambda (f^{T}1)-\lambda (f^{T}f-n)\\ & =f^{T}Lf-\lambda (f^{T}f-n)\end{array}\text{\hspace{1em}(3.5)}$$
因此
$$\begin{array}{rl}\underset{f\in R^n}{\min }L(f,\lambda )\iff & \underset{f\in R^n}{\min }{f}^{T}Lf\\ & s.tf\perp 1(\text{that is }{f}^{T}1=0)\\ & f^{T}f=n(f^{T}f>0)\end{array}$$
现在我们得到无约束且连续的目标函数，由于二次型函数是天然的凸函数亦可导，可以快速找到全局最优解，只需要令其导数为$0$即可得到极值，对向量和矩阵求导详请见《机器学习常用矩阵求导方法》。

①求微分
$$\begin{array}{rl}dL(f,\lambda )& =d[f^{T}Lf-\lambda (f^{T}f-n)]=d(f^{T}Lf-\lambda f^{T}f)\\ & =d(f^T)Lf+f^{T}L(df)-\lambda d(f^T)f-\lambda f^T(df)\\ & =(df{)}^{T}Lf+f^{T}L(df)-\lambda (df{)}^{T}f-\lambda f^T(df)\\ & =tr[(df{)}^{T}Lf+f^{T}L(df)-\lambda (df{)}^{T}f-\lambda f^T(df)]\\ & =tr[(df{)}^{T}Lf]+tr[f^{T}L(df)]-\lambda \cdot tr[(df{)}^{T}f]-\lambda \cdot tr[f^T(df)]\\ & =tr[f^T{L}^T(df)]+tr[f^{T}L(df)]-\lambda \cdot tr[f^T(df)]-\lambda \cdot tr[f^T(df)]\\ & =tr[f^T(L^T+L)(df)-2\lambda f^T(df)]\\ & =[f^T(L^T+L)-2\lambda f^T]df\\ & =[2f^T{L}^T-2\lambda f^T]df\end{array}\text{\hspace{1em}(3.6)}$$
最后一步$2L^T=L^T+L$，是因为$L=D-W$，其中度矩阵$D$和邻接矩阵$W$均为对称矩阵，因此两个对称矩阵的差依然为对称矩阵，即$L^T=L$

②得到导数
由标量微分$dy=f^{\prime }(x)dx$推导出向量微分$dy=(\frac{dy}{dx}{)}^{T}dx$得

$$\begin{array}{rl}\frac{dL(f,\lambda )}{df}& =[2f^T{L}^T-2\lambda f^T{]}^T=2Lf-2\lambda f=0\\ & \Rightarrow Lf=\lambda f\end{array}\text{\hspace{1em}(3.7)}$$
我们得到了一个惊人的结论！！当$Lagrange$乘子$\lambda$是拉普拉斯矩阵$L$的特征值(eigenvalue)且指示向量$f$是$L$的特征向量(eigenvector)时，函数有极值。

那么，这个函数的极值到底是什么呢？我们继续分析，因为目标函数是$f^{T}Lf$，所以我们可以将等式$(3.7)$两边分别左乘$f^T$凑成目标函数形式后为
$$f^{T}Lf=\lambda f^{T}f=\lambda n$$
因为$n=|V|$是常数，显然取决于目标函数值大小的元素是$\lambda$，即
$$\min \frac{f^{T}Lf}{f^{T}f}=\min \lambda \text{\hspace{1em}(3.8)}$$
也就是说$L$的特征值$\lambda$越大，目标函数值越大；特征值$\lambda$越小，目标函数值越小！！随着入坑越深，我们已逐渐将连续优化问题转化成了特征分解问题。那么$\lambda$的最小值是多少呢？我们从两个角度来分析

①拉格朗日乘子角度
在高数中，我们之所以定义$Lagrange$乘子是为了方便求导，即将有约束的连续问题转化为无约束的连续问题，而定义后的$Lagrange$函数就是原函数的下界，即
$$\begin{array}{rl}\min f^{T}Lf& \ge \min L(f,\lambda )\\ & =f^{T}Lf-\lambda f^{T}f\\ & \Rightarrow \lambda \ge 0\end{array}$$
由于$f^{T}f=n>0$，则必然$\lambda \ge 0$，因此我们可满心欢喜地得到结论${\lambda }_{\min }=0$。

②拉普拉斯矩阵性质角度
我们之前在式$(2.8)$推导出，对于指示向量$f\in R^n$有
$$f^{T}Lf=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2$$
由于$w_{ij}\ge 0$，二次项$\ge 0$，因此$f^{T}Lf\ge 0$。又因为$\min f^{T}Lf\iff \min \lambda$，所以${\lambda }_{\min }=0$。

令拉普拉斯矩阵的第二小特征值作为目标函数最优值

那我们是不是直接将${\lambda }_{\min }=0$这个解作为目标函数的解，求出对应特征向量$f$(指示向量)就完事了呢？毫无疑问，它可以作为一个平凡解，但是否是我们想要的解？

显然不是！因为我们定义的目标函数值是有意义的，我们从最初的$Cut(V)$到$RatioCut(V)$都代表着按某种方式切图后的代价。当这个代价为$0$，则表示我们没有切图，所有的样本都属于一类，这种情况下得到的特征向量$f$(指示向量)一定是常数向量$1$。因此，我们一般不取最小而是取第二小特征值$\lambda$作为最优值，其对应的特征向量$f$即为我们所求的最优解。

实数解向量的定性

本节到这里就可以结束了吗？显然还不能TAT，别忘了，我们最初是将离散问题转化成连续问题求解的，也就是说当前目标函数所得到的最优解$f$是任意实数解向量(real-valued solution vector)，我们无法从中断言哪个样本确切的属于哪个类别。因此，我们还需要将实数解向量定性。

对于二聚类$(c=2)$问题，这个很好做，毕竟我们的解向量$f\in R^n$，因此最简单粗暴的定性方法是判断$f_i$是否大于等于0，即

$$\{\begin{array}{l}{v}_i\in A\text{ if }{f}_i\ge 0\\ v_i\in \overline{A}\text{ if }{f}_i<0\end{array}$$

不是总结的总结

回顾我们这一节都干了啥？

①重新确定指示向量$f$并推导出$\min f^{T}Lf\iff \min RatioCut(V)$
②找出目标函数$f^{T}Lf$的3个约束条件，即
$$\begin{array}{rl}& \underset{f\in R^n}{\min }{f}^{T}Lf\\ & s.tf\perp 1\\ & f_i\text{ as defined in Eq.(3.1)}\\ & f^{T}f=n\end{array}$$
③去掉约束$f_i\text{ as defined in Eq.(3.1)}$，将离散问题松弛为连续问题。
④引入拉格朗日乘子将约束问题转化为无约束问题，其中$L(f,\lambda ):=f^{T}Lf-\lambda (f^{T}1)-\lambda (f^{T}f-n)$
⑤通过对无约束问题求导，我们得到$Lf=\lambda f$，并进一步得到
$$\min f^{T}Lf\iff \min \lambda$$
⑥通过从拉普拉斯矩阵性质的分析，我们得知${\lambda }_{\min }=0$，同时其对应特征向量$f$是常数向量$1$，因此我们取第二小特征值作为目标函数最优值，对应特征向量为最优解向量。
⑦将实数解向量$f$定性。

至于多聚类问题该怎么处理请看$3.1.3$节。

3.1.2 总结拉普拉斯矩阵的性质与瑞利商

相信经过前一节的讨论，我们可以更好地理解拉普拉斯矩阵$L$。以下严格来说，我们讨论的是非标准化的$L$。

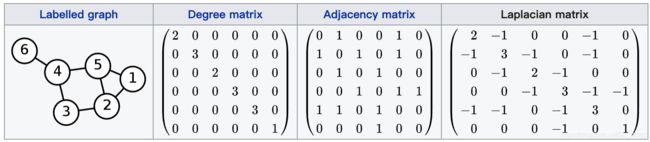
拉普拉斯矩阵(Laplacian matrix)在图论和数学领域，有时也被称为基尔霍夫矩阵(Kirchhoff matrix)，它是图形的矩阵表示形式。它可以用于计算定图的生成树的个数，也可以通过计算第二个最小特征值来近似图的最稀疏切割。

———摘自维基百科

(1) 拉普拉斯矩阵$L$的性质

1. 对于每一个指示向量$f\in R^n$，有$$f^{T}Lf=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}(f_i-f_j{)}^2$$
2. $L$是实数对称矩阵(symmetric)且$L$是半正定矩阵(positive semi-definite)。(解释：对称因为$L=D-W$;半正定因为性质$1$导致$f^{T}Lf\ge 0$)
3. $L$的行和为$0$。(从上图可以看出，如第一行$2-1-1=0$)
4. $L$的最小特征值${\lambda }_{\min }=0$，其对应特征向量是常数向量$1$。(解释：前者可以从$f^{T}Lf=\lambda f^{T}f\ge 0$ (其中$f$为任意非$0$向量)看出；后者是因为当$\lambda =0$时有$f^{T}Lf=0$，且由性质$3$得$L$行和为0，则$f=1$）
5. $L$有$n$个非负实数特征值$\lambda$，且$0={\lambda }_1\le {\lambda }_2\le ...{\lambda }_n$

(2) $\text{L}$的谱($\text{Spectrum}$)以及连通分量的个数

当图$G$是一个仅有非负权重的无向图时，其对应的拉普拉斯矩阵$L$的$0$特征值(0谱)的个数$k$就是图中$A_1,...,A_k$连通分量的个数$k$。$0$特征值对应的特征空间由这些连通分量对应的指示向量$1_{A_1},...,1_{A_k}$张成(span)

(注：连通分量的个数和聚类的个数未必相同，前者是客观存在的，后者是我们可以指定的)

【归纳证明】：

1. 当$k=1$时，即$0$特征值的个数只有一个时，情况如上述性质$4$，所有样本都属于一个类。因此，图中也只有一个连通分量。
2. 当$k=2$时，即图中有两个连通分量，则按这两个连通分量将图中顶点排序后得到的邻接矩阵为分块矩阵，如下图所示：
   $$\begin{array}{c}W=\left(\begin{array}{ccccc}0& w_{12}& w_{13}& 0& 0\\ w_{21}& 0& w_{23}& 0& 0\\ w_{31}& w_{32}& 0& 0& 0\\ 0& 0& 0& 0& w_{45}\\ 0& 0& 0& w_{54}& 0\end{array}\right)=\left(\begin{array}{cc}{W}_1& \\ & W_2\end{array}\right)\end{array}$$
   因此，得到的拉普拉斯矩阵也是分块矩阵(如下图)，而由拉普拉斯矩阵性质$4$可得，每个$L_i$的最小特征值${\lambda }_{\min }=0$，因此$L$的$0$特征值的个数有两个。
   $$L=D-W=\left(\begin{array}{cc}{L}_1& \\ & L_2\end{array}\right)$$
3. 当$k>2$时，即图中有$k$个连通分量时，对应的拉普拉斯矩阵是如下分块矩阵，故可得到$k$个$0$特征值。
   $$L=\left(\begin{array}{cccc}{L}_1& & & \\ & L_2& & \\ & & \ddots & \\ & & & L_k\end{array}\right)$$

(3) 瑞利商($\text{Rayleigh Quotient}$)

看到网上很多有叫瑞利熵的，这里我纠正一下，Quotient表示商的意思，没有entropy的含义好吗？在此之前，我们先简要介绍一下$Hermitian$矩阵。

①$Hermitian$矩阵

$Hermitian$矩阵又被译为厄尔米特矩阵，指的是自共轭矩阵。

【定义】：$n$阶复方阵$A$的对称单元互为共轭(两个实部相等，虚部互为相反数的复数互为共轭复数)，若$A$的共轭转置矩阵$A^H$等于它本身，则