深度学习中的激活函数与损失函数

a. 为什么在神经网络中加入非线性是必须的？

  以下内容参考自神经网络的激活函数为什么要使用非线性函数？

如果使用线性函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。加深神经网络的层数就没有什么意义了。线性函数的问题在于不管加深层数到多少，总是存在与之等效的「无隐藏层」的神经网络。为了稍微直观的理解这一点，考虑下面一个简单的例子。

存在一个线性函数f(x)=kx(k≠0)作为激活函数，将y=f(f(f(x)))对应三层的神经网络。很明显可以想到同样的处理可以由y=ax(a=k^3)，一个没有隐藏层的神经网络来表示。该例子仅仅是一个近似，实际中的神经网络的运算要比这个例子复杂很多，但不影响结论的成立。也就是说，使用线性激活函数时，无法发挥多层网络带来的优势。

相反如果使用非线性函数，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

b.  写出下列每个激活函数的表达式及其导数。绘制原函数及其导数的图像。总结各激活函数的利弊。

•  ReLU:max(0,x)
• Sigmoid: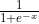,其导数为
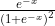
• Tanh: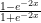，其导数为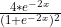

原函数图像为

图一 原函数图像

对应的导数图像为

图2 对应导函数图像

附上在jupyter notebook上绘制图像的程序

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(-5,5)
#原函数
y_sigmoid=1/(1+np.exp(-x))
y_tanh=(1-np.exp(-2*x))/(1+np.exp(-2*x))
y_relu = np.array([0*item  if item<0 else item for item in x ]) 
#导函数
y_sigmoid_dao=np.exp(-x)/(1+np.exp(-x))**2
y_tanh_dao=4*np.exp(-2*x)/(1+np.exp(-2*x))**2
y_relu_dao=np.array([0 if item<0 else 1 for item in x])
#画图
plt.figure(1,figsize=(9,3))
plt.subplot(131)
plt.plot(x,y_relu,'ro')
plt.title('relu')
plt.subplot(132)
plt.plot(x,y_sigmoid,'g*')
plt.title('sigmoid')
plt.subplot(133)
plt.plot(x,y_tanh,'b+')
plt.title('tanh')

plt.figure(2,figsize=(9,3))
plt.subplot(131)
plt.plot(x,y_relu_dao,'ro')
plt.title('relu_dao')
plt.subplot(132)
plt.plot(x,y_sigmoid_dao,'g*')
plt.title('sigmoid_dao')
plt.subplot(133)
plt.plot(x,y_tanh_dao,'b+')
plt.title('tanh_dao')

激活函数区别：

•  梯度特性不同，sigmoid函数和tanh函数的梯度在饱和区非常平缓，接近于0，很容易造成梯度消失的问题，减缓收敛速度。但事物都有两面性，梯度平缓使得模型对噪声不敏感。
• relu函数的梯度大多数情况下是常数，有助于解决深层网络的收敛问题。Relu函数的另一个优势在于其生物方面的合理性，它是单边的，更符合生物神经元的特征。
• 提出sigmoid函数和tanh函数，主要是因为他们全程可导，并且存在表达区间。sigmoid和tanh区间是0到1或者-1到1，在表达上，尤其是输出层表达上有优势。
• Relu更容易学习优化，是因为其分段线性性质，导致其前传、后传、求导都是分段线性，而传统的sigmoid函数，由于两端饱和，在传播中容易丢失信息。

c.分类与回归的区别，以及softmax的作用

图3 回归任务和分类任务的区别

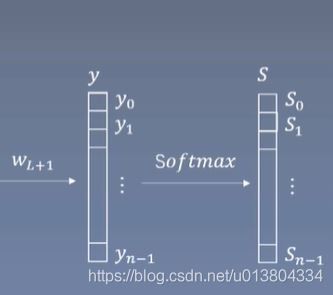
 回归任务如图3 左部所示，模型输出量yi是连续的实数值，分类任务模型如图3 右半部分所示，模型输出的是离散的类别值。分类是在回归模型的基础上完成的。但分类模型多出一个softmax函数，并且分类和回归模型使用不同的损失函数。

假设存在两个数值，a  and b,并且a>b,如果使用max函数取值，那么只能取a的值，不会取到b.这种情况会造成数值小的那个数值饥饿。在某些场景下，我们期望数值大的值能够以较大概率取到，数值小的值也能以较小的概率取到，这个时候我们就需要使用softmax函数。还是同样的两个数值，a>b,如果我们使用softmax函数来计算取a还是取b的概率，那a的softmax值是大于b的，所以a会经常取到，而b偶尔也会取到，取到的概率跟它们本来的数值大小有关。
softmax函数在数学上的定义为：
        数组Y中有j个元素，Yi表示Y中第i个元素，那么Yi的softmax值为：

                                                                                       

        也就是说，是该元素的指数，与所有元素指数和的比值。

相比(−∞,+∞)范围内的分数，概率天然具有更好的可解释性，让后续取阈值等操作顺理成章。经过全连接层，我们获得了K个类别(−∞,+∞)范围内的分数yi，为了得到属于每个类别的概率，先通过e^yi将分数映射到(0,+∞)，然后再归一化到(0,1)，这便是Softmax的思想。

 

d.独立手推CROSS ENTROPY损失函数

推导cross entropy函数之前，我们可以先了解一下KL距离的概念。KL距离，是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)的事件空间，若用概率分布Q（x）编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用D（P||Q）表示KL距离，计算公式如下：

                                                                    

 

对于分类问题来讲，一个样本对应的网络的输出S(s1,s2,...,sn)是一个概率分布，而这个样本的标注一般为(0,0,...,1,0,0,...0)，也可以看作一个概率分布(硬分布)。

cross entropy可以看作是与S之间的KL距离

                                                                     

假设=(0,0,...,1,0,...,0)，其中1为它的第k个元素，(索引从0开始)

求得S=()

则D(||S)==(中只有这一项为1，其它项均为0）,这就是cross entropy函数的一种理解。

神经网络的最后一层通常是softmax函数，它将计算得到的数值映射到(0,1)的区间内，以概率的形式表达模型预测得到的类别，具体形式如图4所示：

图4 softmax层​

 损失函数为   

利用梯度来更新参数时最后一层对y求导，有

                                                     

                                                              

                                                             

写成向量的形式：

 

e. 批量梯度下降，随机梯度下降，小批量梯度下降这三种分别是什么意思，通常会用哪一种？为什么？其他两种的缺点是什么？

1. 批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，也就是方程（1）中的m表示样本的所有个数。
优点：全局最优解；易于并行实现；
缺点：当样本数目很多时，训练过程会很慢。

2. 随机梯度下降法：它的具体思路是在更新每一参数时都使用一个样本来进行更新，也就是方程（1）中的m等于1。每一次跟新参数都用一个样本，更新很多次。如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次，这种跟新方式计算复杂度太高。
但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。
优点：训练速度快；
缺点：准确度下降，并不是全局最优；不易于并行实现。
从迭代的次数上来看，SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。

3.小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）：它的具体思路是在更新每一参数时都使用一部分样本来进行更新，也就是方程(1）中的m的值大于1小于所有样本的数量。为了克服上面两种方法的缺点，又同时兼顾两种方法的优点。

三种方法使用的情况：
如果样本量比较小，采用批量梯度下降算法。如果样本太大，或者在线算法，使用随机梯度下降算法。在实际的一般情况下，采用小批量梯度下降算法。