史上最简SLAM零基础解读(6) - 卡方分布(chi-square distribution)和()卡方检验(Chi-Squared Test) → 理论讲解与推导
本人讲解关于slam一系列文章汇总链接:史上最全slam从零开始
文末正下方中心提供了本人 联系方式, 点击本人照片即可显示 W X → 官方认证 {\color{blue}{文末正下方中心}提供了本人 \color{red} 联系方式,\color{blue}点击本人照片即可显示WX→官方认证} 文末正下方中心提供了本人联系方式,点击本人照片即可显示WX→官方认证
一、前言
我们最终的目的是为了讲解如何在工程上使用卡方检验(Chi-Squared Test) ,在这之前我们需要了解两个重要的知识点,那就是卡方分布(chi-square distribution)和()卡方检验(Chi-Squared Test) 。为了方便大家理解,以通俗的方式进行讲解,然后再引入专业的相关名词。简单的说:
( 1 ) 卡方分布: \color{blue}(1)卡方分布: (1)卡方分布:若n个相互独立的随机变量ξ₁,ξ₂,…,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)
( 2 ) 卡方检验: \color{blue}(2)卡方检验: (2)卡方检验:卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,基本思想是根据样本数据推断总体的频次与期望频次是否有显著性差异,经常通过小数量的样本容量去预估总体容量的分布情况。
先对卡方检验以及对应的一些实例进行简介,然后我们再来探讨卡方分布的由来 \color{red}先对 卡方检验 以及对应的一些实例进行简介,然后我们再来探讨卡方分布的由来 先对卡方检验以及对应的一些实例进行简介,然后我们再来探讨卡方分布的由来,在这之前,我们先来了解一个比较难理解的内容,那就是显著性水平。来看下图:
 在假设检验中,我们经常见到显著性水平这一说法,你可能有疑问了,它出镜率咋那么高,它到底是何方神圣呢?这张图就清晰的展示了,一个总体模型是被分为置信水平和显著性水平两部分。下面会通过一个通俗的例子会会它。
在假设检验中,我们经常见到显著性水平这一说法,你可能有疑问了,它出镜率咋那么高,它到底是何方神圣呢?这张图就清晰的展示了,一个总体模型是被分为置信水平和显著性水平两部分。下面会通过一个通俗的例子会会它。
万能的朋友圈永远不乏微商的身影,而一向讨厌微商的你在平静的某天被一则微商产品所吸引,内容是:“减肥的灵丹妙药,成功率高达90%,女神们一起来吧!”虽然这则广告充满诱惑力,但你依然保持清醒,理智的思考解决对策。一鼓作气,打算自己检测一下宣传内容的真实性。
你随机调查了15个用过此产品的人,发现减肥成功的有12个人。如果广告为真的话,那么减肥成功的应该有15×0.9=13.5,现在12<13.5,你信心十足的告诉其他人不要轻易相信这款减肥产品!但是,你真的能确定它就是一则虚假广告吗?会不会是你自己出了差错呢?这时候,显著性水平就要华丽登场发挥作用了。
假设采用5%的显著性水平进行检验,如果某事件算得的P值小于5%,那它就是一件小概率事件,当小概率事件发生时,你就应该提高警惕了,概率这么小的事件都能遇到,那就有充分的理由拒绝宣传了。
由于试验次数一定,并且你的目标是减肥成功的人数,那么,成功的人数是符合二项分布(重复n次独立的试验,在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变)的,即,此时。
现在计算的P值是大于5%的,所以没有足够的证据证明减肥产品是骗人的,认为减肥成功率有90%(图1形象的展示了它们之间的关系)。所以啊,女神们可以在保证安全的前提下尝试一下这款产品。

对于任何一个问题的检验,我们只能是说有多大的把握去接受某一个假设,其中肯定存在犯错误的概率,而显著性水平就是 能承担该过程中犯错误的水平大小 \color{red}能承担该过程中犯错误的水平大小 能承担该过程中犯错误的水平大小,就像上述减肥产品一样,如果它对效果检测的偏差在我们可接受的范围内,我们依然可以接受产品的宣传。因此,显著性水平是很宽容的,它给了我们一定的犯错误的可能,至于是大是小,那就看自己的冒险精神了。但是不要无限的扩大它,如果允许犯错误的概率高达30%或40%,那研究也就没有意义了。
二、卡方检验(chi-square distribution)→引导示例
为了方便大家的理解,这里先做一个简单的例子,抽奖机,肯定都不陌生,现在一些商场超市门口都有放置。正常情况下出奖概率是一定的,综合来看,商家收益肯定大于支出。
倘若突然某段时间内总是出奖,甚是反常,那么到底是某阶段是小概率事件还是有人进行操作了?抽奖机怎么了?针对这种现象或者类似这种现象问题则可以借助卡方进行检验。下面是某台抽奖机的期望分布,其中X代表每局游戏的净收益(每局独立事件): x -2 23 48 73 98 P=(X=x) 0.977 0.008 0.008 0.006 0.001 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text { \color{Green} x }} & \mathbf {\text { \color{Green} -2 }} & \text { \color{Green} 23} & \text { \color{Green} 48 } & \text { \color{Green} 73 } & \text { \color{Green} 98 }\\ \hline \text { \color{Green} P=(X=x) } & 0.977 & 0.008 & 0.008 & 0.006 & 0.001 \\ \hline \end{array} x P=(X=x) -2 0.977 230.008 48 0.008 73 0.006 98 0.001根据表格我们可以知道,每一局的成本价为两元,也就是说,你玩一局有0.997的概率损失2元,0.008的概率获利23元,依次类推。下面是实际观察中玩家收益的频数为:
x -2 23 48 73 98 频率 965 10 9 9 7 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text { \color{Green} x }} & \mathbf {\text { \color{Green} -2 }} & \text { \color{Green} 23} & \text { \color{Green} 48 } & \text { \color{Green} 73 } & \text { \color{Green} 98 }\\ \hline \text { \color{Green} 频率 } & 965 & 10 & 9 & 9 & 7 \\ \hline \end{array} x 频率 -2 965 2310 48 9 73 9 98 7目的:在5%的显著性水平下,看看能否有足够证据证明判定抽奖机被人动了手脚。一般来说,使用卡方检验(Chi-Squared Test) ,主要包含四个步骤: 1.建立假设检验、2.计算理论值、3.计算卡方值、4. 查卡方表求P值。
1.建立假设检验
检验假设 ( 原假设 ) H 0 : \color{blue}检验假设(原假设)H0: 检验假设(原假设)H0:老虎机每局收益符合如下概率分布:
x -2 23 48 73 98 P=(X=x) 0.977 0.008 0.008 0.006 0.001 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text { \color{Green} x }} & \mathbf {\text { \color{Green} -2 }} & \text { \color{Green} 23} & \text { \color{Green} 48 } & \text { \color{Green} 73 } & \text { \color{Green} 98 }\\ \hline \text { \color{Green} P=(X=x) } & 0.977 & 0.008 & 0.008 & 0.006 & 0.001 \\ \hline \end{array} x P=(X=x) -2 0.977 230.008 48 0.008 73 0.006 98 0.001 备择假设 H 1 : \color{blue}备择假设H1: 备择假设H1:老虎机每局收益不符合如上概率分布,显著水平 α=0.05。
也就是说这表明,当作出接受原假设的决定时,其正确的可能性(概率)为95%。
2.计算理论值
根据原假设,如果进行了1000局老虎机游戏,那么他的频数理论上应该如下:
x -2 23 48 73 98 频率 977 8 8 6 1 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text { \color{Green} x }} & \mathbf {\text { \color{Green} -2 }} & \text { \color{Green} 23} & \text { \color{Green} 48 } & \text { \color{Green} 73 } & \text { \color{Green} 98 }\\ \hline \text { \color{Green} 频率} & 977 & 8 & 8 & 6 & 1 \\ \hline \end{array} x 频率 -2 977 238 48 8 73 6 98 1
下面是实际观察中玩家收益的频数为:
x -2 23 48 73 98 频率 965 10 9 9 7 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text { \color{Green} x }} & \mathbf {\text { \color{Green} -2 }} & \text { \color{Green} 23} & \text { \color{Green} 48 } & \text { \color{Green} 73 } & \text { \color{Green} 98 }\\ \hline \text { \color{Green} 频率 } & 965 & 10 & 9 & 9 & 7 \\ \hline \end{array} x 频率 -2 965 2310 48 9 73 9 98 7下面我们把理论表格与实际表格进行合并,如下:
x 观察频数 期望频数 -2 965 977 23 10 8 48 9 8 73 9 6 98 7 1 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text {\color{Green} x }} & \mathbf {\text {\color{Green} 观察频数 }}&\mathbf {\text { \color{Green} 期望频数 }}\\ \hline \text { \color{Green} -2} & ~965 & ~~977 \\ \hline \text { \color{Green} 23} & ~10 & ~~8 \\ \hline \text { \color{Green} 48} & ~9 & ~~8 \\ \hline \text { \color{Green} 73} & ~9 & ~~6 \\ \hline \text { \color{Green} 98} & ~7 & ~~1\\ \hline \end{array} x -2 23 48 73 98 观察频数 965 10 9 9 7 期望频数 977 8 8 6 1
3.计算卡方值
卡方检验求卡方的公式如下: χ 2 = ∑ ( A − T ) 2 T (01) \color{Green} \tag {01} \chi^{2}=\sum \frac{(A-T)^{2}}{T} χ2=∑T(A−T)2(01)
其中,A为实际值,T为理论值,x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
①实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
②差异程度与理论值的相对大小
那么带入实际值与理论值,计算过程如下:
χ 2 = ( 965 − 977 ) 2 977 + ( 10 − 8 ) 2 8 + ( 9 − 8 ) 2 8 + ( 9 − 6 ) 2 6 = ( 7 − 1 ) 2 1 = 38.272 (02) \color{Green} \tag {02} \chi^{2}=\frac{(965- 977)^2} {977}+\frac{(10 - 8)^2}{8}+ \frac{(9 -8)^2} {8} + \frac{(9 - 6)^2} {6} = \frac{(7 - 1)^2} {1} =38.272 χ2=977(965−977)2+8(10−8)2+8(9−8)2+6(9−6)2=1(7−1)2=38.272(02)
4.查卡方表求P值
根据自由度,与显著水平查询检验统计量临界值.
自由度 : \color{blue}自由度: 自由度:其主要和表格的行数列数相关,这里的表格指实际观测的表格,并且一般频数需要以列的形式呈现,也即是前面实际观测的表格,应该转换为以下形式:
x 观察频数 -2 965 23 10 48 9 73 9 98 7 \begin{array}{|l|l|l|l|l|l|} \hline \mathbf {\text {\color{Green} x }} & \mathbf {\text {\color{Green} 观察频数 }}\\ \hline \text { \color{Green} -2} & ~965 \\ \hline \text { \color{Green} 23} & ~10 \\ \hline \text { \color{Green} 48} & ~9 \\ \hline \text { \color{Green} 73} & ~9 \\ \hline \text { \color{Green} 98} & ~7\\ \hline \end{array} x -2 23 48 73 98 观察频数 965 10 9 9 7
对于单行或单列:自由度 = 组数-限制数,为5组,限制数为1,也就是 5-1=4。对于表格类:自由度 = (行数 - 1) * (列数 - 1)。后面我们会讲解一个多行多列的例子。现在我们根据自由度4,以及前面的显著水平 α=0.05。在如下表格中(F表示自由度)进行查找:

那么其拒绝域为 χ > 9.14 \chi>9.14 χ>9.14,也就是说检验统计量大于9.49 位于拒绝域内。我们计算出来的 χ 2 = 38.272 \chi^2=38.272 χ2=38.272,明显是其是大于9.14的,也就是其位于拒绝域内,另外:
如果位于拒绝域内我们拒绝原假设H0,接受H1。
如果不在拒绝域内我们接受原假设H0,拒绝H1
于是拒绝原假设,也就是说抽奖机被人动了手脚。现在大家肯定还有一个疑惑,那就是上面的这个表格,是怎么来的,为了巩固知识,我们先再简介一个例子,再来推导上面的表格,也就是方分布(chi-square distribution)
二、卡方检验(chi-square distribution)→再度示例
以下为一个典型的四格卡方检验,我们想知道喝牛奶对感冒发病率有没有影响:
感冒人数 末感冒人数 合计 感冒率 喝牛奶组 43 96 139 30.94 % 不喝牛奶组 28 84 112 25.00 % 合计 71 180 251 28.29 % \begin{array}{|l|l|l|l|l|} \hline & \mathbf {\text { \color{Green} 感冒人数 }} & \text { \color{Green} 末感冒人数 } & \text { \color{Green} 合计 } & \text { \color{Green} 感冒率 } \\ \hline \text { \color{Green} 喝牛奶组 } & 43 & 96 & 139 & 30.94 \% \\ \hline \text { \color{Green} 不喝牛奶组 } & 28 & 84 & 112 & 25.00 \% \\ \hline \text { \color{Green} 合计 } & 71 & 180 & 251 & 28.29 \% \\ \hline \end{array} 喝牛奶组 不喝牛奶组 合计 感冒人数 432871 末感冒人数 9684180 合计 139112251 感冒率 30.94%25.00%28.29%
1.建立假设检验
检验假设 H 0 : \color{blue}检验假设H0: 检验假设H0:喝牛奶与感冒没有关系。
备择假设 H 1 : \color{blue}备择假设H1: 备择假设H1:喝牛奶与感冒存在关系,显著性水平 α=0.01
2.计算理论值
基于 假设H0,喝牛奶与感冒没有关系,那么喝牛奶组与不喝牛奶组,他们感冒的几率应该是一样的,也就是理论表格应该如下:
感冒人数 末感冒人数 合计 喝牛奶组 39.3231 99.6769 139 不喝牛奶组 31.6848 80.3152 112 合计 71 180 251 \begin{array}{|l|l|l|l|} \hline & \text { \color{Green} 感冒人数 } & \text { \color{Green} 末感冒人数 } & \text { \color{Green} 合计 } \\ \hline \text { \color{Green} 喝牛奶组 } & 39.3231 & 99.6769 & 139 \\ \hline \text { \color{Green} 不喝牛奶组 } & 31.6848 & 80.3152 & 112 \\ \hline \text { \color{Green} 合计 } & 71 & 180 & 251 \\ \hline \end{array} 喝牛奶组 不喝牛奶组 合计 感冒人数 39.323131.684871 末感冒人数 99.676980.3152180 合计 139112251那么很明显实际值与理论值,存在一定差距。
3.计算卡方值
χ 2 = ( 43 − 39.3231 ) 2 39.3231 + ( 28 − 31.6848 ) 2 31.6848 + ( 96 − 99.6769 ) 2 99.6769 + ( 84 − 80.3152 ) 2 80.3152 = 1.077 (03) \color{Green} \tag {03} \chi^{2}=\frac{(43 - 39.3231)^2} {39.3231}+\frac{(28 - 31.6848)^2}{31.6848}+ \frac{(96 - 99.6769)^2} { 99.6769} + \frac{(84 - 80.3152)^2} { 80.3152} = 1.077 χ2=39.3231(43−39.3231)2+31.6848(28−31.6848)2+99.6769(96−99.6769)2+80.3152(84−80.3152)2=1.077(03)
4.查卡方表求P值
首先计算自由度,这里用r表示表格的行数,c表示表格的列数,如下图:
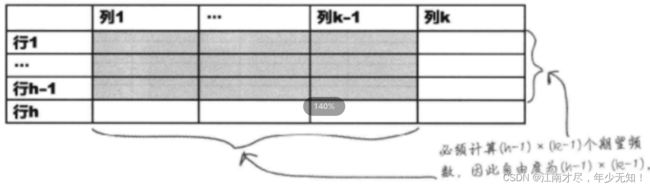 那么自由度的公式为:
那么自由度的公式为:
v ( 自由度 ) = ( r − 1 ) ( c − 1 ) (04) \color{Green} \tag {04} v(自由度)=(r-1)(c-1) v(自由度)=(r−1)(c−1)(04)带入数据计算的 v = ( r − 1 ) ( c − 1 ) = ( 2 − 1 ) ∗ ( 2 − 1 ) = 1 v=(r-1)(c-1)=(2-1)*(2-1)=1 v=(r−1)(c−1)=(2−1)∗(2−1)=1,再结合前面的显著性水平 α=0.01,查询表格临界值为 6.64(在前面卡方分布表中查找),很明显我们计算出来的 χ 2 = 1.077 \chi^{2}=1.077 χ2=1.077 低于该值,也就是其没有位于拒绝域内,那么我们接受原假设H0,喝牛奶与感冒没有关系。下面我们就来看看我们查询的表格是怎么来的。
四、卡方分布(chi-square distribution)
先把博客前面的话拿过来→卡方分布:若n个相互独立的随机变量ξ₁,ξ₂,…,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)
也就是说,卡方分布是建立在n个相互独立的随机变满足正态分布的前提下,