支持向量机(SVM)

支持向量机(Support Vector Machine)是一种十分常见的分类器，曾经火爆十余年，分类能力强于NN，整体实力比肩LR与RF。核心思路是通过构造分割面将数据进行分离。本文主要阐述SVM的基本工作原理和简单应用。

SVM的分类

线性可分SVM

线性可分SVM的原理是要达到硬边界最大化。这里的线性可分是指，当我们想用一个分割平面，将两个数据分割开时，存在至少一个分割面，使两个数据可以完全分离，则我们认为这个SVM是线性可分SVM。

线性SVM

线性SVM是指，分割面虽然不能完全分割所有数据，但是该线性分割方式可以使绝大多数数据正确的被分类。那么这样的SVM也可以被称为线性SVM。线性SVM要达到的是软边界最大化。这里的“软”对应线性可分SVM的“硬”。硬边界指的是支持向量到分割面的距离，因为支持向量距离分割面最近，该距离也是过渡带宽度（的一半）。而软边界指的是，当SVM不是线性可分的情况时，此时支持向量并不一定是距离分割面最近的向量。因此SVM此时并不能一味地边界最大化，而是使过渡带足够宽。此时的边界最大化并不是真正意义上的，严格的边界最大化。所以用软进行区分。

非线性SVM

对于前两种SVM，对其加入一个核函数就可以构造出非线性SVM。

SVM原理

超平面

在二维空间里，对于一条直线：$w_1{x}_1+w_2{x}_2+b=0$，$(w_1,w_2)$实际上就是直线的法线方向。如果我们代入$(x_1,x_2)$到等式左边，则当该式大于0时，点$X$在法线正方向上，小于0时则在法线负方向上，等于0则在法线上。将这一性质应用于更高维度的话，此时点$X$就是一个$n$维向量，而这条直线也就变为超平面了。

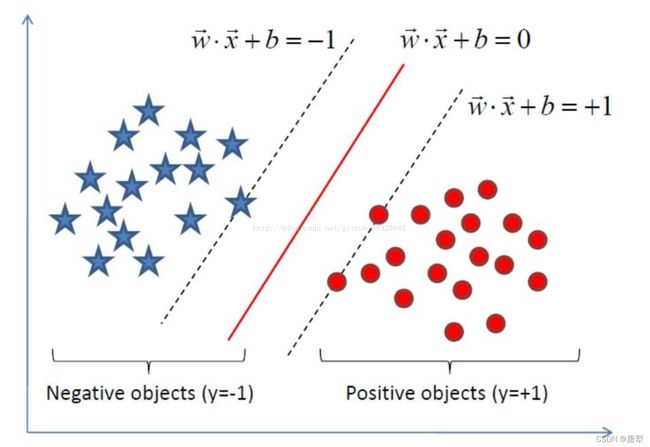
支持向量

支持向量怎么选择？以线性可分SVM为例，我们将$w$认为是若干样本线性组合得到的，第$1$个样本为$x_1$，第$i$个为$x_i$。对于每个$x$，给予其系数$\alpha$，此时存在：$w={\sum }_i^n{\alpha }_i{x}^{(i)}$，选取部分$\alpha$，使它们的值不为$0$，其余值都设为$0$。则对$w$真正起作用的就是值不为$0$的这些$x$向量。这些向量，支持了法线向量，因此就是支持向量。

若直线$l$有参数$w$和$b$，通过计算每个样本到直线$l$距离，衡量哪条直线是最为合适的分割线。距离$d$可以表示为：$d=\frac{w{x}^{(i)}+b}{\Vert w\Vert }$，若每个数据集中样本的形式为$T=\{(x_1,y_1)(x_2,y_2)\dots (x_n,y_n)\}$，而每个样本的$y$值，就是这个样本的label。正例为$1$，负例为$-1$。这里的正负值其实反映的就是样本位于分割线的方向。位于法线正方向即为正。将$y$值一起乘入等式右边：$d=\frac{w{x}^{(i)}+b}{\Vert w\Vert }{y}^{(i)}$，这里的$y$值是样本的实际正负值，如果估计值与实际值符号相同，即分类正确，此时的结果为正值。如果分类错误，则结果为负值。

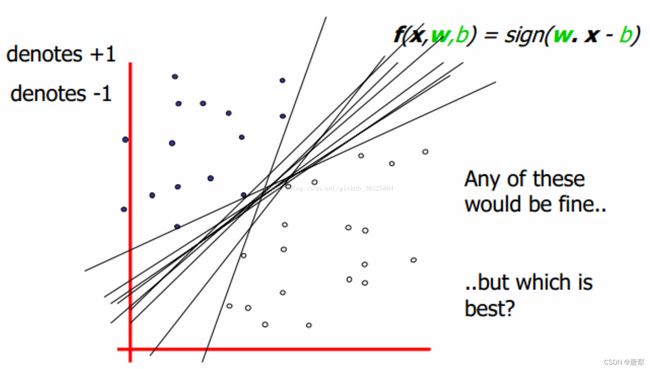
构造分割面

在所有样本中，距离该直线最近的样本应被选为支持向量。支持向量与直线间的距离即为过渡带。因为SVM期望过渡带尽可能大，因此最终参数$w$与$b$的选择可以表示为：
$$w^{\ast },b^{\ast }=\mathrm{argmax}(\underset{i=1,2,...,n}{\min }\frac{w{x}^{(i)}+b}{\Vert w\Vert }{y}^{(i)})$$
因此，给定线性可分训练数据集，通过间隔最大化得到的分割超平面为：$y(x)=w^T\Phi (x)+b$，相应的分类决策函数为：$f(x)=sign(w^T\Phi (x)+b)$。

目标函数

对于线性可分SVM而言，目标函数实际上就是分割平面的选取，因此目标函数实际上就是：
$$w^{\ast },b^{\ast }=\underset{w,b}{\mathrm{argmax}}(\frac{1}{\Vert w\Vert }\underset{i=1,2,...,n}{\min }(y^{(i)}w{x}^{(i)}+b))$$
对于上式，在不改变分割面位置的情况下，总存在一个$w$值，使距离该直线最近的向量到直线距离为$1$。因此上式中，最小值部分可以始终取$1$。此时的$W$值，实际上才是目标函数本身，此时存在约束条件：$y^{(i)}(W^T\Phi (x^{(i)})+b)\ge 1$。因此，通过拉格朗日乘子法可以对目标函数求极值：
$$\begin{gathered} \underset{w,b}{\max }\frac{1}{\Vert w\Vert }, \\ s.t.y^{(i)}(W^T\Phi (x^{(i)})+b)\ge 1,i=1,2,...,n \end{gathered}$$
变形后可得：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2, \\ s.t.y^{(i)}(W^T\Phi (x^{(i)})+b)\ge 1,i=1,2,...,n \end{gathered}$$
对目标函数使用拉格朗日乘子法：
$$\begin{gathered} L(w,b,a)=\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}^n{a}^{(i)}(1-y^{(i)}(w^T\Phi (x^{(i)})+b)), \\ s.t.1-y^{(i)}(W^T\Phi (x^{(i)})+b)\le 0,i=1,2,...,n \end{gathered}$$
这里的$w$和$b$是原始的参数，而$a$是引入的参数且大于等于$0$。为了方便整理与化简，接下来对$L$求偏导并使偏导为0：
$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})=0$$
解得：
$$\begin{array}{rl}w& =\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})\\ \frac{\partial L}{\partial b}& =-\sum _{i=1}^n{a}^{(i)}{y}^{(i)}=0\end{array}$$
根据上式，$a$等于$0$的时候可知其对$w$与$b$无作用。因此，真正的支持向量，是那些不为$0$的向量。

这里给出一个通过凸优化后最终得到的求的式子：
$$a^{\ast }=\underset{a}{\mathrm{argmax}}(\sum _{i=1}^n{a}^{(i)}-\frac{1}{2}\sum _{i,j=1}^n{a}^{(i)}{a}^{(j)}{y}^{(i)}{y}^{(j)}{\Phi }^T(x^{(i)}){\Phi }^T(x^{(j)}))$$
求出$a$之后回代可得$w$与$b$：
$$\begin{array}{rl}{w}^{\ast }& =\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})\\ b^{\ast }& =y^{(i)}-\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})\Phi (x^{(j)})\end{array}$$

松弛因子

对于线性SVM而言，因为不要求所有样本都被分对，因此其约束条件和线性可分SVM并不相同。给出一个大于等于$0$的松弛因子$\xi$，使函数间隔加上松弛因子后大于等于$1$，此时有目标函数及约束条件：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^n{\xi }^{(i)}, \\ s.t.y^{(i)}(W^T\Phi (x^{(i)})+b)\ge 1-{\xi }^{(i)},i=1,2,...,n \end{gathered}$$
上式中，$C$是一个控制松弛因子权重的参数。当$C$足够大时，$\xi$只能趋近于0，变回线性可分SVM。因此上式也可以被看作是线性可分SVM的扩展。松弛项可以被理解为线性回归中的正则项，$C$的值越小，过渡带越宽，$C$的值越大，过渡带越窄。这也使得线性SVM具备更强的泛化性。

同样的，对于线性SVM的目标函数及其约束条件使用拉格朗日乘子法后，求偏导可得：
$$L(w,b,\xi ,a,\mu )=\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^n{\xi }^{(i)}+\sum _{i=1}^n{a}^{(i)}(1-y^{(i)}(w^T\Phi (x^{(i)})+b)-{\xi }^{(i)})-\sum _{i=1}^n{\mu }^{(i)}{\xi }^{(i)}$$
$$\begin{array}{rl}\frac{\partial L}{\partial w}& =w-\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})=0\\ w& =\sum _{i=1}^n{a}^{(i)}{y}^{(i)}\Phi (x^{(i)})\\ \frac{\partial L}{\partial b}& =-\sum _{i=1}^n{a}^{(i)}{y}^{(i)}=0\\ \frac{\partial L}{\partial \xi }& =C-a^{(i)}-{\mu }^{(i)}\end{array}$$
这里直接给出$a$最后的求解形式：
$$\begin{gathered} a^{\ast }=\underset{a}{\mathrm{argmin}}(\sum _{i=1}^n{a}^{(i)}-\frac{1}{2}\sum _{i,j=1}^n{a}^{(i)}{a}^{(j)}{y}^{(i)}{y}^{(j)}{\Phi }^T(x^{(i)}){\Phi }^T(x^{(j)})) \\ s.t.\sum _{i=1}^n{a}^{(i)}{y}^{(i)}=0 \\ 0\le a^{(i)}\le C,i=1,2,...,n \end{gathered}$$

损失函数

SVM的损失，通常被定义为没有被正确分在过渡带外面的向量，到过渡带边界的距离。位于过渡带内的样本，损失为$1-d$。$d$是该样本到分割面的距离。注意，如果是在“本方”过渡带，则$d$为正值。如果已经越过分割面了，则$d$值变为负值。这个损失也被称为Hinge损失。因此损失函数可以被写成：
$$Loss(w,b)=\sum _{i=1}^n{\xi }^{(i)}$$
换句话说，松弛因子本身可以被看作是损失的衡量。因为松弛因子本身也是包容分割面的分割错误。实际上，损失本身，就是由于线性SVM允许过渡带内存在向量，甚至向部分错误分类的向量妥协的结果。因此，原目标函数变为：
$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^n{\xi }^{(i)}$$
某种意义上，可以认为是Hinge损失加上一个$l_2$正则。

核函数

核函数可以说是SVM的精髓所在，其目的在于，通过将原始输入空间映射到更高维度的特征空间这一操作，原本线性不可分的样本可以在新的核空间内变为线性可分。常见的核函数有：

• 多项式核函数：$k(x_1,x_2)=(x_1^T{x}_2+c{)}^d$
• RBF核函数：$k(x_1,x_2)=e^{-\frac{\Vert x_1-x_2{\Vert }^2}{2{\sigma }^2}}$
• Sigmoid核函数：$k(x_1,x_2)=\tanh (x_1^T{x}_2+c)$
  从多项式核函数讲起，最基本的，$c$等于$0$，$d$等于$2$的情况下，kernel使原有的两个变量两两相乘。这相当于将维度数量平方了。规模上，特征数目变为平方级，而计算复杂度并没有显著上升。

RBF则是固定每一个$x_i$，对于变化的$x_j$，以$x_i$为中心做指数级衰减。相当于是以$x_i$为中心，做高斯分布。因此被称作高斯核函数。对于每个样本的label而言，正例被核函数向上拉升，负例向下延伸。从而使数据分离。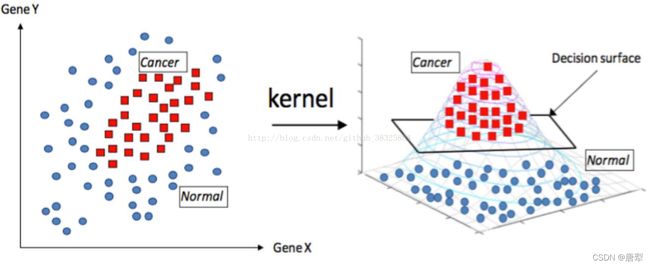
分离后的数据，可以被多个分割面分离，我们要选取的，实际上就是使距离分割面最近的样本距离尽可能大的分割方式。因此最终的超平面选取还是使用线性SVM的思路。RBF的维度映射可以被理解是无穷维的，因为在数学上，RBF的指数可以被泰勒展开。展式中的每一项，都可以被理解为该维度上的样本分离。因为其强力的高维映射能力，RBF往往是首选核函数。

Iris数据分类代码

数据选用的是Iris数据集，代码如下：

import sklearn.datasets
import numpy as np
import pandas as pd
from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

iris = sklearn.datasets.load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris['data'], iris['target'], random_state=1, train_size=0.8)

svm_model = svm.SVC(C=0.5, kernel='linear', decision_function_shape='ovr')
svm_model.fit(x_train, y_train.ravel())

print(accuracy_score(y_train, svm_model.predict(x_train)))
print('Accuracy:', accuracy_score(y_test, svm_model.predict(x_test)))
print(y_test.ravel())
print(svm_model.predict(x_test))

总结

SVM可以说是泛化能力很强的优质分类器，准确率也很高。相比于LR和RF，SVM难点在于调参。RF更多的注重效率，在模型训练以及特征选择上省下了大把时间。LR学习速率也快于SVM，比较通用，精确度和效率都不错。