基于BP_Adaboost的强分类器设计
本文代码将在最后给出
文章目录
- 一、算法介绍
- 二、案例介绍和模型建立
-
- 2.1案例介绍
- 2.2模型建立
- 三、MATLAB编程实现
-
- 3.1 代码实现
-
- 3.1.1数据导入和选择
- 3.1.2弱分类器学习分类
- 3.1.3强分类器学习分类和结果统计
- 3.1.4结果分析
- 3.2 案例拓展
-
- 3.3.1数据导入和选择
- 3.3.2弱预测器学习预测
- 3.3.3强预测器预测
- 3.3.4结果分析
一、算法介绍
Adaboost算法的思想是合并多个“弱”分类器的输出以产生有效分类。其主要步骤为:首先给出弱学习算法和样本空间 ( x , y ) (x,y) (x,y),从样本空间中找出 m m m组训练数据,每组训练数据的权重都是 1 m \frac{1}{m} m1。然后用弱学习算法选代运算 T T T次,每次运算后都按照分类结果更新训练数据权重分布,对于分类失败的训练个体赋予较大权重,下一次迭代运算时更加关注这些训练个体。弱分类器通过反复迭代得到一个分类函数序列 f 1 , f 2 , ⋅ ⋅ ⋅ , f r f_1,f_2,···,f_r f1,f2,⋅⋅⋅,fr,每个分类函数赋予一个权重,分类结果越好的函数,其对应权重越大。 T T T次迭代之后,最终强分类函数 F F F由弱分类函数加权得到。BP_Adaboost模型即把BP神经网络作为弱分类器,反复训练BP神经网络预测样本输出,过Adaboost算法得到多个BP神经网络弱分类器组成的强分类器。
二、案例介绍和模型建立
2.1案例介绍
公司财务预警系统是为了防止公司财务系统运行偏离预期目标而建立的报警系统,具有针对性和预测性等特点。它通过公司的各项指标综合评价并预测公司财务状况、发展趋势和变化,为决策者科学决策提供智力支持。
财务危机预警指标体系中的指标可分为 表内信息指标、盈利能力指标、偿还能力指标、成长能力指标、线性流量指标和表外信息指标六大指标,每项大指标又分为若干小指标,如盈利能力指标又可分为净资产收益率、总资产报酬率、每股收益、主营业务利润率和成本费用利润率等。在用于公司财务预警预测时,如果对所有指标都进行评价后综合,模型过于复杂,并且各指标间相关性较强,因此在模型建立前需要筛选指标。
指标筛选分为显著性分析和因子分析两步。显著性分析通过T检验方法分析ST公司和非ST公司,在财务指标中找出差别较大、能够明显区分两类公司的财务指标。因子分析在显著性分析基础上对筛选出来的指标计算主成分特征值,从中找出特征值大的指标作为公司危机预警方法的最终评价指标。最终找出成分费用利润率、资产营运能力、公司总资产、总资产增长率、流动比率、营业现金流量、审计意见类型、每股收益、存货周转率和资产负债率十项指标作为评价指标,该十项指标能够比较全面地反映出公司的财务状况。
2.2模型建立
算法流程图如下:
算法步骤如下:
-
数据选择和网络初始化。从样本空间中随机选择 m m m组训练数据,初始化测试数据的分布权值 D t ( i ) = 1 m D_t(i)=\frac{1}{m} Dt(i)=m1,根据样本输入输出维数确定神经网络结构,初始化BP神经网络权值和阔值。
-
弱分类器预测。训练第 t t t个弱分类器时,用训练数据训练BP神经网络并且预测训练数据输出,得到预测序列 g ( t ) g(t) g(t)的预测误差和 e t e_t et,误差和 e t e_t et的计算公式为
e t = ∑ i D i ( i ) i = 1 , 2 , 3 , ⋅ ⋅ ⋅ , m ( g ( t ) ≠ y ) e_t = \sum\limits_iD_i(i) \quad\quad i = 1,2,3,···,m(g(t)\neq y) et=i∑Di(i)i=1,2,3,⋅⋅⋅,m(g(t)=y)
式中, g ( t ) g(t) g(t)为预测分类结果; y y y为期望分类结果。 -
计算预测序列权重。根据预测序列 g ( t ) g(t) g(t)的预测误差 e t e_t et,计算序列的权重 α t \alpha_t αt,权重计算公式为
α t = 1 2 l n ( 1 − e t e t ) \alpha_t = \frac{1}{2}ln(\frac{1-e_t}{e_t}) αt=21ln(et1−et) -
测试数据权重调整。根据预测序列权重 α t \alpha_t αt,调整下一轮训练样本的权重,调整公式为
D t + 1 ( i ) = D t ( i ) B t ∗ e − α t y i g t ( x i ) i = 1 , 2 , ⋅ ⋅ ⋅ , m D_{t+1}(i) = \frac{D_t(i)}{B_t}*e^{-\alpha_ty_ig_t(x_i)}\quad\quad i = 1,2,···,m Dt+1(i)=BtDt(i)∗e−αtyigt(xi)i=1,2,⋅⋅⋅,m
式中, B t B_t Bt是归一化因子,目的是在权重比例不变的情况下使分布权值和1。
5.强分类函数。训练 T T T轮后得到 T T T组弱分类函数 f ( g t , α t ) f(g_t,\alpha_t) f(gt,αt),由 T T T组弱分类函数 f ( g t , α t ) f(g_t,\alpha_t) f(gt,αt)组合得到了强分类函数 h ( x ) h(x) h(x)。
h ( x ) = s i g n [ ∑ t = 1 T α t ⋅ f ( g t , α t ) ] h(x) = sign[\sum\limits_{t = 1}^T\alpha_t·f(g_t,\alpha_t)] h(x)=sign[t=1∑Tαt⋅f(gt,αt)]
对于本案例来说,共有1350组公司财务状况数据,每组数据的输入为10维,代表上述的10个指标,输出为1维,代表公司财务状况,为1时表示财务状况良好,为-1时表示财务状况出现问题。从中随机选取1000组数据作为训练数据,350组数据作为测试数据。根据数据维数,采用的BP神经网络结构为10-6-1,共训练生成10个BP神经网络弱分类器,最后用10个弱分类器组成强分类器对公司财务状况进行分类。
三、MATLAB编程实现
3.1 代码实现
3.1.1数据导入和选择
%% 清空环境变量
clc
clear
%% 下载数据
load data input_train output_train input_test output_test
%% 权重初始化
[mm,nn]=size(input_train);
D(1,:)=ones(1,nn)/nn;
3.1.2弱分类器学习分类
把BP神经网络看作弱分类器,经过训练后分类训练样本,并且根据训练样本分类结果调整训练样本权重值,最终得出一系列弱分类器及其权重。为了体现出强分类器的分类效果,本例降低了BP 神经网络训练次数以降低弱分类器分类能力。
%% 弱分类器分类
K=10;
for i=1:K
%训练样本归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
error(i)=0;
%BP神经网络构建
net=newff(inputn,outputn,6);
net.trainParam.epochs=5;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00004;
%BP神经网络训练
net=train(net,inputn,outputn);
%训练数据预测
an1=sim(net,inputn);
test_simu1(i,:)=mapminmax('reverse',an1,outputps);
%测试数据预测
inputn_test =mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu(i,:)=mapminmax('reverse',an,outputps);
%统计输出效果
kk1=find(test_simu1(i,:)>0);
kk2=find(test_simu1(i,:)<0);
aa(kk1)=1;
aa(kk2)=-1;
%统计错误样本数
for j=1:nn
if aa(j)~=output_train(j);
error(i)=error(i)+D(i,j);
end
end
%弱分类器i权重
at(i)=0.5*log((1-error(i))/error(i));
%更新D值
for j=1:nn
D(i+1,j)=D(i,j)*exp(-at(i)*aa(j)*test_simu1(i,j));
end
%D值归一化
Dsum=sum(D(i+1,:));
D(i+1,:)=D(i+1,:)/Dsum;
end
3.1.3强分类器学习分类和结果统计
%% 强分类器分类结果
output=sign(at*test_simu);
%% 分类结果统计
%统计强分类器每类分类错误个数
kkk1=0;
kkk2=0;
for j=1:350
if output(j)==1
if output(j)~=output_test(j)
kkk1=kkk1+1;
end
end
if output(j)==-1
if output(j)~=output_test(j)
kkk2=kkk2+1;
end
end
end
disp('第一类分类错误 第二类分类错误 总错误');
% 窗口显示
disp([kkk1 kkk2 kkk1+kkk2]);
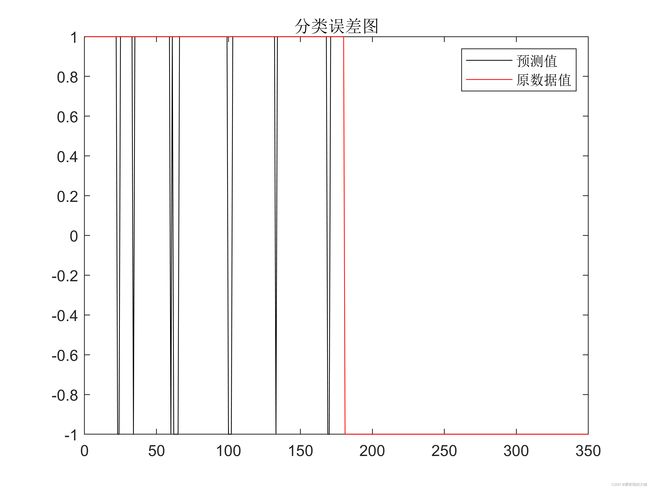
plot(output,'k')
hold on
plot(output_test,'r')
title('分类误差图')
legend('预测值','原数据值')
%统计弱分离器效果
for i=1:K
error1(i)=0;
kk1=find(test_simu(i,:)>0);
kk2=find(test_simu(i,:)<0);
aa(kk1)=1;
aa(kk2)=-1;
for j=1:350
if aa(j)~=output_test(j);
error1(i)=error1(i)+1;
end
end
end
disp('统计弱分类器分类效果');
error1
disp('强分类器分类误差率')
(kkk1+kkk2)/350
disp('弱分类器分类误差率')
(sum(error1)/(K*350))
3.1.4结果分析
| 强分类器误差率 | 弱分类器误差率 |
|---|---|
| 4% | 5.46% |
从上表可以看出,强分类器分类误差率低于弱分类器分类误差率,表明BP_Adaboost分类算法取得了良好的效果。
3.2 案例拓展
Adaboost方法不仅可以用于设计强分类器,还可以用于设计强预测器。强预测器设计思路与强分类器设计类似,都是先赋予测试样本权重,然后根据弱预测器预测结果调整测试样本权重并确定弱预测器权重,最后把弱预测器序列作为强预测器。不同的是在强分类器中增加预测错类别样本的权重,在强预测器中增加预测误差超过國值的样本权重。采用BP_Adaboost强预测器预测第2章中非线性函数输出,函数形式为 y = x 1 2 + x 2 2 y=x_1^2+x_2^2 y=x12+x22。
3.3.1数据导入和选择
%% 清空环境变量
clc
clear
%% 下载数据
load data1 input output
%% 权重初始化
k=rand(1,2000);
[m,n]=sort(k);
%训练样本
input_train=input(n(1:1900),:)';
output_train=output(n(1:1900),:)';
%测试样本
input_test=input(n(1901:2000),:)';
output_test=output(n(1901:2000),:)';
%样本权重
[mm,nn]=size(input_train);
D(1,:)=ones(1,nn)/nn;
%训练样本归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
3.3.2弱预测器学习预测
把BP神经网络看作弱预测器,经过训练后预测测试样本输出,并且根据预测结果调整样本测试样本权重值,最终得出一系列弱预测器及其权重。这里把预测误差超过0.1的测试样本作为应该加强学习的样本。
K=10;
for i=1:K
%弱预测器训练
net=newff(inputn,outputn,5);
net.trainParam.epochs=20;
net.trainParam.lr=0.1;
net=train(net,inputn,outputn);
%弱预测器预测
an1=sim(net,inputn);
BPoutput=mapminmax('reverse',an1,outputps);
%预测误差
erroryc(i,:)=output_train-BPoutput;
%测试数据预测
inputn1=mapminmax('apply',input_test,inputps);
an2=sim(net,inputn1);
test_simu(i,:)=mapminmax('reverse',an2,outputps);
%调整D值
Error(i)=0;
for j=1:nn
if abs(erroryc(i,j))>0.2 %较大误差
Error(i)=Error(i)+D(i,j);
D(i+1,j)=D(i,j)*1.1;
else
D(i+1,j)=D(i,j);
end
end
%计算弱预测器权重
at(i)=0.5/exp(abs(Error(i)));
%D值归一化
D(i+1,:)=D(i+1,:)/sum(D(i+1,:));
end
3.3.3强预测器预测
%% 强预测器预测
at=at/sum(at);
%% 结果统计
%强分离器效果
output=at*test_simu;
error=output_test-output;
plot(abs(error),'-*')
hold on
for i=1:8
error1(i,:)=test_simu(i,:)-output;
end
plot(mean(abs(error1)),'-or')
title('强预测器预测误差绝对值','fontsize',12)
xlabel('预测样本','fontsize',12)
ylabel('误差绝对值','fontsize',12)
legend('强预测器预测','弱预测器预测')
3.3.4结果分析
分类结果图如下所示
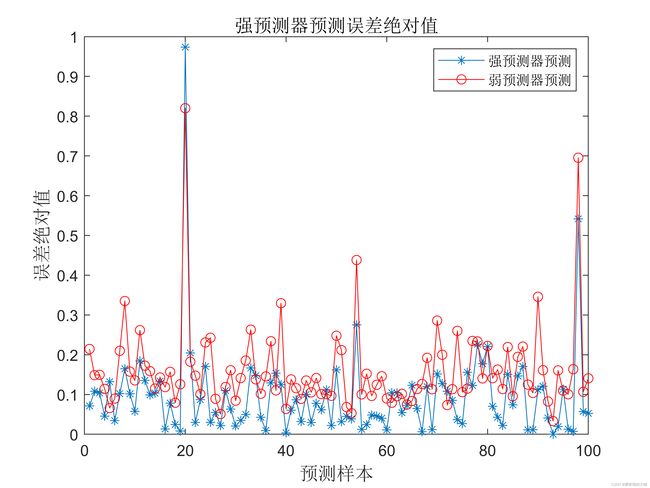
预测样本共有350组,共有10个BP神经网络构成弱预测器序列,强预测器分类误差绝
对值和弱预测器预测平均误差绝对值如上图所示。
从上图可以看出,强预测器预测误差低于弱预测器预测误差,BP_Adaboost强预测器预测算法取得了良好的效果。
代码链接:https://pan.baidu.com/s/1fRslPHoxDgXp4OCf2Mjovg
提取码:6666
引用:
MATLAB神经网络43个案例