目标跟踪 SiamFC++ （Towards Robust and Accurate Visual Tracking with Target Estimation Guidelines）

文章标题：《SiamFC++：Towards Robust and Accurate Visual Tracking with Target Estimation Guidelines》
文章地址：https://arxiv.org/abs/1911.06188
github地址：https://github.com/MegviiDetection/video_analyst

2020年 AAAI（Proceedings of the AAAI Conference on Artificial Intelligence） 的一篇文章。
作者来自浙大和旷视。

---

引言

现在很多基于深度学习的跟踪都被当做一个分类任务来做，对于给定的目标，要同时得到鲁棒的分类和准确的状态估计。以往大家提出了许多不同方法来进行目标状态估计，但是他们很少考虑到视觉跟踪问题本身的特殊性。经过仔细的分析，我们提出了一系列准则，用于指导设计高效的目标跟踪器。我们根据以下 4 条准则设计了全卷积暹罗跟踪器++（Fully Convolutional Siamese tracker++，SiamFC++）。(G1) 同时引入 ‘分类’ 分支和 ‘状态估计’ 分支。(G2) 明确的分类得分。(G3) 无先验知识地跟踪。(G4) 估计质量的得分。

（ps：这里说的 ‘状态估计’ 我觉得就是指坐标回归：Location、Regression）

大量的分析和消融实验证明了上述准则的有效性。没有花哨的功能，我们的 SiamFC++ 跟踪器在五个具有挑战性的基准测试（OTB2015，VOT2018，LaSOT，GOT-10k，TrackingNet）上实现了最先进的性能，这证明了跟踪器的跟踪和泛化能力。特别是，在大规模的 TrackingNet 数据集上，SiamFC++ 在超过 $90$ FPS 的情况下，实现了之前未见过的 $75.4$ 的 AUC 得分，这远远超过了实时要求。

1. 介绍

通常来说，视觉跟踪要做的是，在信息非常有限的情况下（例如只有被跟踪对象的第一帧的坐标），要在后续视频帧上连续定位它的位置。它是许多计算机视觉问题中的基本模块，例如用于无人机的跟随和其它监控系统中。通用的目标跟踪有一个特点，就是没有先验知识，不知道跟踪的对象是什么，也不知道它周围是什么样的环境。

跟踪问题可以被看做是分类（classification）任务和估计（estimation）任务的结合。第一个任务主要通过 ‘分类’ 对目标提供一个鲁棒的粗略的定位。第二个任务就接着来估计它的准确状态。虽然现代跟踪器已经取得了很大的进步，但令人惊讶的是，它们对于第二项任务（即目标状态估计）的方法却有很大的不同。根据这一点，它们的方法可以分为以下 $3$ 个种类：
（1） DCF 和 SiamFC，粗鲁地用多尺度测试，又不准确，效率又低。另外，它们预先假设了固定的尺度比例和变化率，这在实际变化中通常是不成立的。
（2）ATOM，通过梯度上升，迭代地调整多个初始边界框（bounding boxes）来估计目标位置，这大大提高了准确性。然而这种目标估计方法不仅计算量大，而且附加超参数较多（例如初始框的数量和分布），不好调参。
（3）SiamRPN 系列，通过引入区域建议网络（Region Proposal Network，RPN）达到准确和高效的状态估计。然而，预定义的锚点（Anchor）设置不仅引入了模糊的相似度评分，严重阻碍了鲁棒性，而且还需要知道数据分布的先验信息，这明显不符合通用跟踪器的初衷。

根据上述分析，我们提出了高性能通用跟踪器的设计准则：

$\bullet$ G1: 把分类和状态估计分开 (decomposition of classification and state estimation)
跟踪器应该进行两个子任务：分类和状态估计。如果没有强大的分类器，跟踪器就无法从背景或干扰物中区分目标，这严重阻碍跟踪器的鲁棒性。没有准确的估计结果，跟踪器的准确性从根本上受到限制。那些粗鲁的多尺度测试方法很大程度上忽略了后一项任务，存在效率低、准确性低等问题。

$\bullet$ G2：无歧义评分 (non-ambiguous scoring)
分类得分应该直接表明目标在 “视场” 中是否存在，例如说，是否在对应像素的子窗口里。而不是用像锚点框这类预先定义的设置。作为一个负面例子，在目标与锚点框之间进行匹配（例如 anchor-based RPN branch）容易产生假阳性（false positive）结果，导致跟踪失败。

$\bullet$ G3：无先验知识 (prior knowledge-free)
通用跟踪器应该不受尺度、比例分布等先验知识的影响，现有方法普遍存在对数据分布先验知识的依赖，影响了算法的泛化能力。

$\bullet$ G4：估计 ‘质量评估’ (estimation quality assessment)
直接依据分类得分来选择边界框（bounding box）会导致性能下降。应该再用一个独立于分类得分的 ‘质量评估’ 得分。以前有一些人就是这么做的，增加一个这样的分支，得到了惊人的准确性，例如 ATOM 和 DiMP。

根据上述准则，我们设计了 SiamFC++。输出特征图的每个像素直接对应搜索图（就是那个输入x）上的子窗口。根据 G1，我们增加了一个回归头，用于进行准确的目标状态估计，这个回归头和分类头是并行的。由于预定义的锚点框被移除了，就没有了 G2 中的模糊匹配，也没有了 G3 中关于目标尺度和比例分布的先验知识。最后，根据 G4，再增加一个质量评估头。

我们的贡献可以总结为以下三个方面：
（1）通过分析跟踪问题的特点，我们为现代跟踪器的设计提供了一套目标状态估计的实用指导思想。
（2）我们应用这些准则，设计了一个简单但是功能强大的 SiamFC++ 跟踪器。大量的实验和全面的分析证明了我们提出的指导准则的有效性。
（3）我们的方法在五个具有挑战性的基准上取得了最先进的结果。据我们所知，我们的SiamFC++ 是第一个在大规模数据集（TrackingNet ）运行速度超过 $90$ FPS、AUC得分达到 $75.4$ 的跟踪器。

2. 相关工作

略…

3. SiamFC++

(图1)

3.1 Siamese-based Feature Extraction and Matching （暹罗特征提取和匹配）

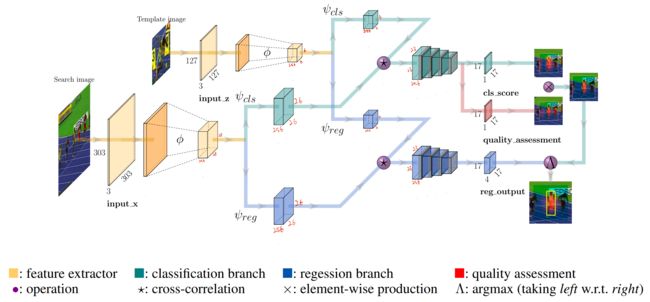
目标跟踪任务可以看做是相似度学习（similarity learning）问题。具体来说，我们离线训练一个暹罗网络，然后通过在线评估，在一个更大的搜索图（search image）上定位我们的模板图（template image）。暹罗网络由两个分支组成，template 分支以 $z$ 作为输入，它是从第一帧图像中，目标所在位置裁剪出来的图像块。search 分支采用当前帧作为输入，记为 $x$。两个分支共用同一个骨干（backbone），它对输入 $z$ 和 $x$ 进行同样的转换，把它们嵌入到同一个特征空间中，用于后续的任务。模板图和搜索图在嵌入空间 $\varphi$ 上进行相关（cross-correlation）：
$$f_i(z,x)={\psi }_i(\varphi (z))\star {\psi }_i(\varphi (x))，i\in \{\text{cls, reg}\}\text{\hspace{1em}(1)}$$

其中 $\star$ 表示相关操作（cross-correlation）。$\varphi (.)$ 表示用骨干网络提取通用特征。${\psi }_i(.)$ 表示特定的任务层，用 $i$ 指明哪个任务（$\text{cls}$ 表示分类，$\text{reg}$ 表示回归）。在我们的实现中，对模板图的 ${\psi }_{\text{cls}}(.)$和对搜索图的 ${\psi }_{\text{cls}}(.)$ 是两个不一样的卷积层，另外两个 ${\psi }_{\text{reg}}(.)$也是如此。另外，对同一个图的 ${\psi }_{\text{cls}}(.)$ 和 ${\psi }_{\text{reg}}(.)$ ，输出尺寸是一样的。（详情看上面的图）

3.2 Application of Design Guidelines in Head Network （网络头的设计）

基于 SiamFC，我们根据指导准则， 逐个部分来改进。

根据 G1，模板图和搜索图在特征空间进行相关之后，我们设计了分类头和回归头。对于特征图上的每一个像素，分类头对每个对应的图像块进行分类，判断它是正类还是负类。回归头输出一个 offset 来预测边界框的位置。具体见图(2)。

具体来说，对于分类任务，一个在分类头输出特征图上坐标为 $P_{\text{cls}}=(x,y)$ 的点，它对应于输入搜素图上的点是 $(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys,)$，如果这个点落在 ground-truth box 内，这个这个点 $P_{\text{cls}}$ 应该被认为是正样本，否则就是个负样本。这里 $s$ 是骨干网络的总步长（total stride of backbone），可以认为是下采样倍数，本文中 $s=8$，即 $303÷2^3=37.875\approx 28$
（由于这里没有Padding，所以最后实际得到的会小一点，实际计算的时候从特征图返回到原图时要加上一个偏置）。

对于回归任务，回归头输出特征图上坐标为 $P_{\text{reg}}=(x,y)$ 的点，这个点上有 $4$ 个通道，用一个 $4\text{D}$ 向量 ${\mathbf{t}}^{\ast }=(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$ 表示 。它对应于输入搜索图上的点是 $(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys,)$，设这个点为 $P_l$ ，这个点上记录了它自己所在坐标的左上右下值。${\mathbf{t}}^{\ast }$ 负责预测对应的点 $P_l$ 自己的坐标与 ground-truth bounding box 的 $4$ 坐标偏移值。对于点 $P_{\text{reg}}$，我们的回归输出结果 $(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$ 可以由以下式子规定：
$$\begin{array}{l}{l}^{\ast }=\left(\lfloor \frac{s}{2}\rfloor +xs\right)-x_0，t^{\ast }=\left(\lfloor \frac{s}{2}\rfloor +ys\right)-y_0\\ \\ r^{\ast }=x_1-\left(\lfloor \frac{s}{2}\rfloor +xs\right)，b^{\ast }=y_1-\left(\lfloor \frac{s}{2}\rfloor +ys\right)\end{array}\text{\hspace{1em}(2)}$$

其中 $(x_0,y_0)$ 和 $(x_1,y_1)$ 表示与点 $(x,y)$ 关联的 ground-truth bounding box $B^{\ast }$ 的左上角和右下角坐标。

在分类头和回归头的输出特征图上，每个位置 $(x,y)$ 都对应于输入搜索图上的位置 $(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys,)$ 。根据 G2，我们直接对相应的图像块进行分类，在该位置上回归目标框，这和之前的一些跟踪器的做法一样。换句话说，我们的 SiamFC++ 直接把 locations 视为训练样本。别人那些基于锚点框（anchor-based）的做法把输入图像上的位置当做许多锚点框的中心，在同一个位置输出多个分类得分，对这些锚点框进行坐标回归，这样会导致 anchor 与目标之间的模糊匹配。在我们的逐像素预测方式中，最终特征图上的每个像素只做一个预测。因此每个分类分数都直接表示目标是否在对应像素的子窗口的置信度，我们的设计在这种程度上是没有歧义的。

由于 SiamFC++ 是根据位置来做分类和回归的，不需要依赖预先定义的锚点框，因此不需要关于数据分布的先验知识（例如尺度和比例），这符合 G3。

在上述章节中，我们还没有考虑目标状态的估计质量，直接用了分类得分来选择最终的框。这会导致定位准确性的下降，分类得分没有很好地和定位准确性关联起来，在输出特征图像素点对应的输入子窗口上，中心点附近的重要性比周围的要大。因此，我们假设围绕物体中心的特征像素比其他特征像素具有更好的估计质量。根据 G4，我们添加了一个简单而有效的质量评估分支，和分类头一样，用一个 $1\times 1$ 卷积输出多一块特征图。这块特征图的输出用于估计中心度得分（Prior Spatial Score，$\text{PSS}$），其定义如下：
$${\text{PSS}}^{\ast }=\sqrt{\frac{\min (l^{\ast },r^{\ast })}{\max (l^{\ast },r^{\ast })}\times \frac{\min (t^{\ast },b^{\ast })}{\max (t^{\ast },b^{\ast })}}\text{\hspace{1em}(3)}$$

$\text{PSS}$ 并不是质量评估的唯一选择，作为一个变量，我们也可以预测真实框和预测框之间的 $\text{IoU}$ 得分：
$${\text{IoU}}^{\ast }=\frac{\text{Intersection}(B,B^{\ast })}{\text{Union}(B,B^{\ast })}\text{\hspace{1em}(4)}$$

其中 $B$ 是预测的包围框， $B^{\ast }$ 是对应的真实标签框。

在推理过程中，将预测出来的分类得分和对应位置的 $\text{PSS}$ 相乘，然后依据这个最终的得分来选择包围框。 这样一来，远离目标中心点的包围框会被降低权值，提高了跟踪的准确性。

3.2 Training Objective （训练目标）

损失函数如下：
$$\begin{array}{rl}L(\{p_{x,y}\},q_{x,y},\{{\mathbf{t}}_{x,y}\})=& \frac{1}{N_{\text{pos}}}\sum _{x,y}{L}_{\text{cls}}(p_{x,y},c_{x,y}^{\ast })\\ & +\frac{\lambda }{N_{\text{pos}}}\sum _{x,y}{1}_{\{c_{x,y}^{\ast }>0\}}{L}_{\text{quality}}(q_{x,y},q_{x,y}^{\ast })\\ & +\frac{\lambda }{N_{\text{pos}}}\sum _{x,y}{1}_{\{c_{x,y}^{\ast }>0\}}{L}_{\text{reg}}({\mathbf{t}}_{x,y},{\mathbf{t}}_{x,y}^{\ast })\end{array}\text{\hspace{1em}(5)}$$

其中
$1_{\{.\}}$ 是一个指示函数，如果括号里的式子成立，那么函数的值为 $1$，反之为 $0$。
$L_{\text{cls}}$ 表示 $\text{focal loss}$ ，用于对分类做损失。
$L_{\text{quality}}$ 表示二值交叉熵（binary cross entropy，BCE），用于对质量评估做损失。
$L_{\text{reg}}$ 表示 $\text{IoU}$ 损失，用于边界框坐标回归的损失。
如果位置 $(x,y)$ 上被认为是正样例，则 $c_{x,y}^{\ast }$ 的值为 $1$，对于负样例，$c_{x,y}^{\ast }$ 的值为 $0$。

4.Experiments （实验）

4.1 Implementation Details （实现细节）

4.1.1 Model settings （模型设置）

本文用不同的网络骨干，做了两个版本的跟踪器：
（1）backbone 用改造过的 AlexNet，记为 SiamFC++ - AlexNet。
（2）backbone 用 GoogLeNet，记为 SiamFC++ - GoogLeNet。

其中 GoogLeNet 的计算成本比之前的 ResNet-50 更低，而在基准测试上与 ResNet-50 的性能相同甚至更好。
这些网络都在 ImageNet 上做了预训练，经证明，对于跟踪任务来说都是非常实用的。

4.1.2 Training data （训练数据）

我们采用 ILSVRC-VID/DET，COCO，Youtube-BB，GOT-10k 作为基本训练集。对于视频数据集，我们从 VID，LaSOT，GOT-10k 上选取一对一对的图片，每一对图片来自同一个视频序列，两张图片的间隔不超过 $100$ 帧（Youtube-BB 是 $5$ 帧）。对于图像数据集（COCO，Imagenet-DET）我们弄一些负样本（两张图片是不同的目标）作为训练数据的一部分，来提高模型识别区分干扰物的能力。作为数据增强技术，我们在搜索图像上按照均匀分布进行随机移动和缩放。

4.1.3 Training phase （训练阶段）

对于 AlexNet 的版本，我们冻结 conv1 到 conv3 的参数， 微调 conv4 和 conv5。对于那些没有预训练权重的网络层，我们采用零中心的高斯分布（zero-centered Gaussian distribution）进行初始化，标准差为 $0.01$。首先用 $5$ 个 epoch 对网络进行预热训练，学习率从 $10^{-7}$ 线性上升到 $2\times 10^{-3}$ 。然后用余弦退火学习率（cosine annealing learning rate）调整剩下的 $45$ 个 epochs，每个 epoch 用 $600,000$ 个图像对。用动量为 $0.9$ 的随机梯度下降（SGD）作为优化器。

对于 GoogLeNet 的版本，我们冻结 stage $1$ 和 $2$ 的参数，微调 $3$ 和 $4$。基础学习率增加到 $2\times 10^{-2}$，骨干网络的学习率的大小设为全局学习率的 $0.1$。每个 $epoch$ 的图像对数量减少为 $300,000$ 对，epoch 总数减少为 $20$（其中 $5$ 个 epoch 用于预热，$15$ 个 epoch 用于训练），在第 $10$ 个 epoch 时解冻骨干网络的参数以防止过拟合。对于 LaSOT 的基准实验，我们冻结骨干网络的参数，将每个 epoch 的图像对进一步降低至 $150,000$ 对，使训练数据量相对较少的训练得以稳定。

在 VOT2018 的 sort-term 基准测试中，用 AlexNet 作为骨干的跟踪器运行速度为 $160$ FPS，用 GoogLeNet 的运行速度为 $90$ FPS，用的 GPU 都是 NVIDIA RTX 2080Ti。

4.1.4 Test phase （测试阶段）

模型的输出是一系列包围框，以及它们对应的得分 $s$。基于每个框的尺度和比例的变化，以及它们与最后一帧预测目标位置的距离，对得分进行惩罚。根据惩罚后的得分来选择最终的结果，更新目标状态。

4.2 From SiamFC towards SiamFC++ （从 SiamFC 到 SiamFC++ ）

虽然它们两者都用了逐个像素预测的方式，但是 SiamFC 和我们的 SiamFC++之间存在显著的性能差距。在本小节中，我们对 VOT2018 数据集进行了消融研究，以 SiamFC 为基线，旨在找出改善跟踪性能的关键部分。

(表1)

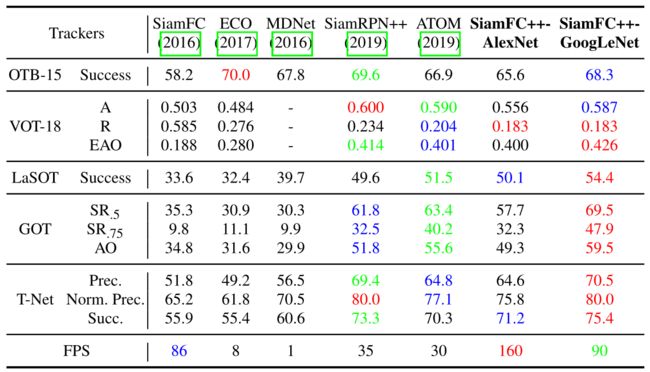
如 (表1) 所示，在 SiamFC++ 基线中，跟踪器只做分类任务，目标状态估计是用多尺度测试来做的。我们逐渐对它添加额外训练数据（第 $2$,$4$ 行），采用一个更好的网络头（第 $3$ 行），增加回归头升级成我们的 SiamFC++（第 $5$ 行）。进一步地，还把骨干从 AlexNet 换成了 GoogLeNet 来更好地提取视觉特征（第 $6$ 行）。

下面以降序地方式罗列影响跟踪器性能的关键组件：回归分支（$0.094$），数据源的多样性（$0.063/0.010$），更强的骨干（$0.026$），更好的网络头结构（$0.02$），其中括号里面表示这些组件带来的 $\Delta \text{EAO}$。注意这些额外组件都是来自建立在 SiamFC 之上的 SiamRPN++。在 SiamFC 上添加了所有这些组件后，我们的 SiamFC++ 以更少的计算预算实现了优异的性能。此外，值得一提的是：(1) 第 $2$ 行的鲁棒性 ($\text{R}$) 超过了 SiamRPN ($0.46$)；(2) 第 $3$ 行的 $\text{R}$ 与 DaSiamRPN ($0.337$) 水准相同，但是用了更少的数据（没有用COCO 和 DET）。这些结果表明，引入 RPN 和 Anchor 无疑会提高精度，但其鲁棒性并没有得到提高，甚至受到阻碍。可以认为这是由于它们违反了我们提出的设计准则。

4.3 Quality Assessment Choice （质量评估的选择）

在 GOT-10k 的验证集上，通过对SiamFC++ - GoogLeNet进行实验，用 $\text{PSS}$ 的方法达到 $77.8$ 的 AO，用 $\text{IoU}$ 的方法达到 $78.0$ 的 AO。 我们在最后的实现中采用 $\text{PSS}$ ，因为在实验中发现它跨数据集的稳定性较好。

4.4 Results on Several Benchmarks（一些基准上的结果）

(表2)

4.4.1 Results on OTB2015 Benchmark

作为目标跟踪最经典的基准之一，OTB 基准为所有跟踪器家族提供了一个公平的测试。我们在包含 $100$ 个视频的 OTB2015 上进行实验，用于跟踪器性能评估。成功得分为$0.682$，与其他跟踪器相比，我们的跟踪器达到了最先进的水平。

4.4.2 Results on VOT Benchmark

VOT2018 包含 $60$ 个视频序列，包含几个具有挑战性的主题，包括快速运动、遮挡等。我们提出的两个版本的跟踪器和当前最先进的跟踪器都有得一比。在相同的速度下，AlexNet 版本要比其他的跟踪器性能都好，GoogLeNet 版本的也不相上下。此外，我们的跟踪器在鲁棒性方面具有明显的优势。据我们所知，这是第一个在 VOT2018 基准测试中，以超过 $100$ FPS的速度运行，$\text{EAO}$ 达到 $0.400$ 的跟踪器，这证明了它在实际生产中应用的潜力。

4.4.3 Results on LaSOT Benchmark

LaSOT（Large scale Single Object Tracking）拥有大量的视频序列，在协议 I（Protocol I ）下有 $1400$ 个序列，协议 II（Protocol II ）下有 $280$ 个序列 ，这使得跟踪器不可能在它上面过拟合，因此可以测试目标跟踪的真实性能。在 Protocol II 下，跟踪器在 train 集上训练，在 test 集上验证，我们的 SiamFC++ 实现了更好的性能，甚至超过了那些在 VOT2018 上比我们好的。这表明基准数据集的规模会影响跟踪器的排名。

4.4.4 Results on GOT-10k Benchmark

对于目标类别的泛化性测试，我们在 GOT-10k（Generic Object Tracking-10k） 上进行训练和测试。这个数据集不仅是一个大规模的数据集（ train 集上有 $10,000$ 种视频， val 集和 test 集上都分别有 $180$ 种），它还在类别不确定性的要求方面对通用跟踪器提出了挑战，因为在 train 子集和 test 子集之间没有类别的交集。我们遵循 GOT-10k 的规则，仅在 train 集上训练。我们的 AlexNet 版本在 test 集上达到了 $53.5$ 的 $\text{AO}$ 值，比 SiamRPN++ 高了 $1.7$，我们的 GoogLeNet 版本达到了 $59.5$ 的 $\text{AO}$ 值，比用在线更新方法的 ATOM 还高。这表明我们的跟踪器具有一定的泛化能力，即使跟踪对象在训练时并没出现过。

4.4.5 Results on TrackingNet Benchmark

我们在 TrackingNet 的 test 集提供的 $511$ 个视频上进行验证。为了避免数据的泄露，我们从训练数据中排除掉 Youtube-BB。这个数据集从 $3$ 个方面对跟踪器进行评价：成功率（success rate），精度（precision），标准化精度（normalized precision）。我们的 GoogLeNet 版本达到了当前最先进的性能，AlexNet 版本在性能和速度之前取得了平衡。

---

具体实施

网络输入数据的选取

(图2)

如上图所示，进入 Siamese 网络的两张图片是这样来的。模板图可以不变，搜索图根据每一次的跟踪结果重新裁剪缩放而来。另外，作者源码实现里没有做数据的标准化（减均值，除方差）。

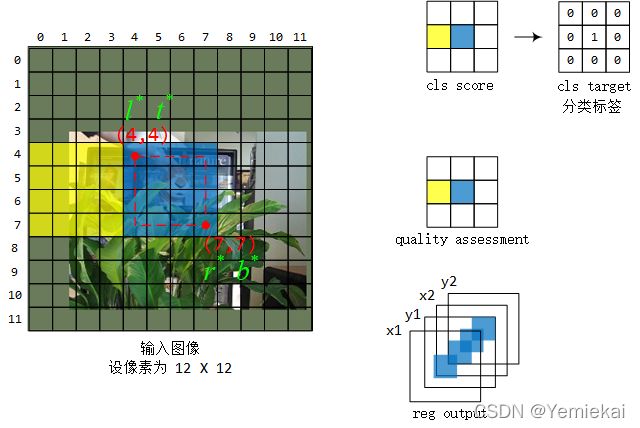
为了方便描述，这里假设输入图像的像素为 $12\times 12$，$4$ 倍下采样，输出特征图的尺寸是 $3\times 3$。

(图3)

根据下采样倍数的关系，输出特征图上 $1$ 个格子对应原图上一个 $4\times 4$ 的区域。
比如输出特征图中蓝色的格子对应原图中间那个 $4\times 4$ 的蓝色区域。
该目标（ground-truth bounding box）的中心点落在蓝色区域内，在分类回归中，则该格子为正样本，于是得到分类标签。

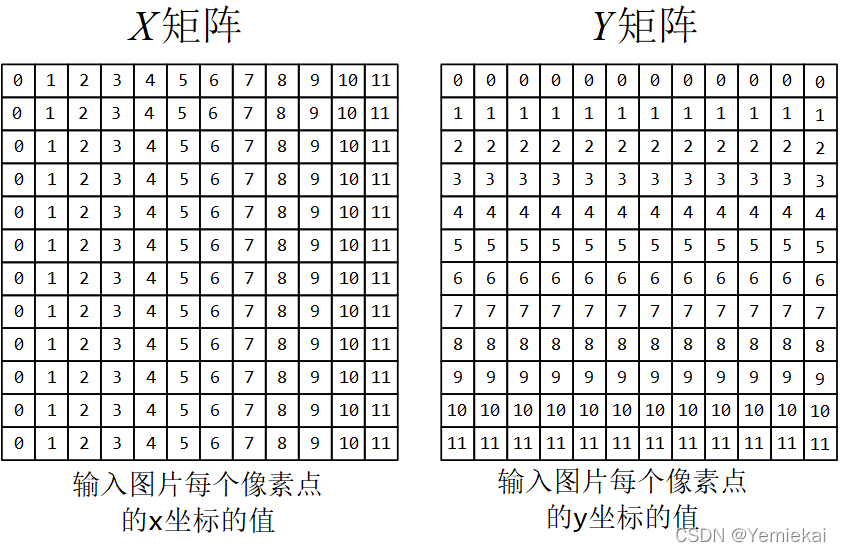
用两个矩阵记下输入图像每个像素点的 $x$ 坐标 和 $y$ 坐标：

(图4)

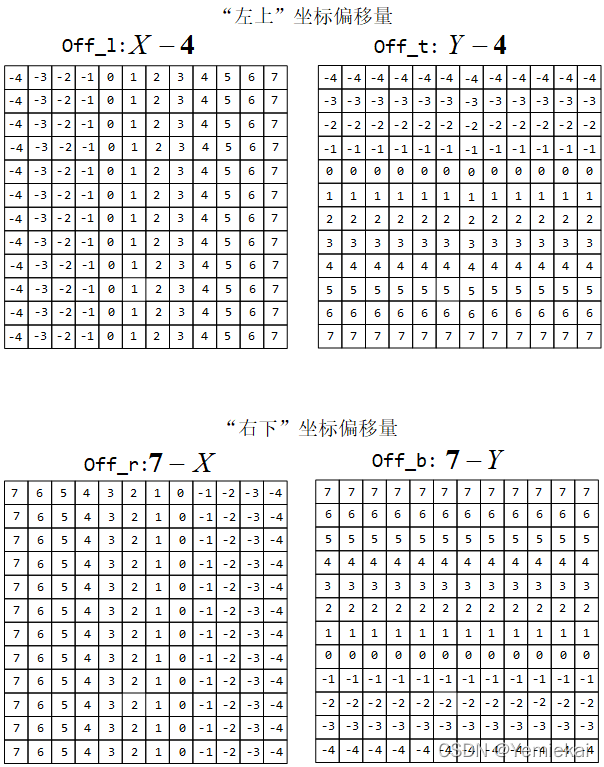
由于我们 bounding box 的坐标表示法用的是 “左上” ，“右下” ，用 $X$ 矩阵减去 ground-truth bounding box 的 $l^{\ast }$ 和 $r^{\ast }$，用 $Y$ 矩阵减去 $t^{\ast }$ 和 $b^{\ast }$，就能得到每个像素点对于真实框的坐标的偏移量。

实际操作时用 $(X-l^{\ast })$，$(r^{\ast }-X)$，$(Y-t^{\ast })$，$(b^{\ast }-Y)$ 得到输入图片的每个像素点对于 ground-truth bounding box 的 “左上” ，“右下” 两个坐标点（共 $4$ 个坐标值 ）的偏置。

(图5)

根据上面提到的公式（3），用所有的偏置算出 ${\text{PSS}}^{\ast }$ 作为质量评估：
（这里直接贴用代码跑的结果，懒得画图了）

(图6)

设输出特征图上的像素点坐标为 $(x,y)$ ，根据公式

$$\begin{array}{r}{x}^{\prime }=\text{offset}+x\times \text{total\_stride}\\ y^{\prime }=\text{offset}+y\times \text{total\_stride}\end{array}\text{\hspace{1em}(6)}$$

算出该特征图的点对应于输入图像的点，取那个位置的值作为 target。
其中 $\text{offset}$ 是由于卷积或下采样时没有 padding 造成的。
$\text{offset}=\left((\text{x\_size}-1)-(\text{score\_size}-1)\ast \text{total\_stride}\right)//2$

这个例子里 $\text{x\_size}=12$，$\text{score\_size}=3$，$\text{total\_stride}=4$
算出来 $\text{offset}=1$。

根据 (公式6) 算出特征图对应于原图上的坐标，取上面的值。

例如：
特征图上 $(x,y)=(0,0)$ 的格子对应原图 $(x^{\prime },y^{\prime })=(1,1)$ 的格子。
特征图上 $(x,y)=(1,1)$ 的格子对应原图 $(x^{\prime },y^{\prime })=(5,5)$ 的格子。

quality assessment 的标签：

(图7)

regression 的标签：

(图8)

这样就能得到所有的 target，后面用来和网络的预测输出做损失，就能进行训练了。

---

反过来验证一下：

cls_score 特征图的每个像素和 quality assessment 特征图的每个像素相乘，得分最高的像素点坐标为 $(1,1)$，根据（公式6）它对应于原图的坐标为 $(5,5)$ 的格子。

在 reg_output 特征图上也选择坐标为 $(1,1)$ 上的值。
于是算出来目标框为
“左上”： $(x_0,y_0)=（5-x_1,5-x_2）=(4,4)$
“右下”： $(x_1,y_1)=（5+y_1,5+y_2）=(7,7)$
得到和（图2）中红色框相同的坐标。