深度学习笔记------循环神经网络RNN

抽象模型

马尔可夫性

这是一个概率论的概念，即：
$P(x_{t+1}|...,x_{t-1},x_t)=P(x_{t+1}|x_t)$
通俗的解释就是关于时间的事件序列x，其发生的状态的情况仅仅与当前时刻的事件有关与更早的事件是无关的。这一性质描述了一个随机过程无记忆的特性。

马尔可夫链

上面定义无记忆的过程也定义了马尔可夫链，也就是对应的$x_t$为离散时间马尔可夫链，对应的下一时间的状态仅仅与当前的状态相关，相关量的数量为1，如果推广一下到2，3，4，5…于是有当下一时间的状态与过去发生过的两个时间序列相关为：
$P(x_3|x_0,x_1,x_2)=P(x_3|x_1,x_2)$
$P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)P(x_4|x_2,x_3)$
其对应为二阶的马尔可夫链，同样更大阶数的马尔可夫链也是相同的方法推导。

最终我们获得了一个通过之前多个时间序列来推导下一时间序列的抽象模型。

循环神经网络

与全连接神经网络不同，RNN体现了一种时间相关性，而其时间相关性的实现便是通过隐藏状态体现，隐藏状态记录了之前时间步的信息，之后传递到下一时间步参与运算，如此往后，循环进行，以此实现一个时序相关的计算过程。

模型

循环神经网络的结构具有很高的重复性，相比于卷积与全连接其显得比较规整，也正因为规整与重复的结构才对应了相应的循环运算。

图中的x为输入，h为产生的隐藏状态，每个单元之间的箭头都是上一单元的隐藏状态，注意$x_t$是某一时间的状态序列，可能是单变量的一个值，也可能是多变量的数据，描述时间点的相关信息。

核心

其中核心的计算就是关于隐藏变量的计算过程，这里与一般的神经网络进行类比:
全连接中的运算是一个线性运算之后进行一个激活函数
$H=\varphi (X{W}_i+b_i)$，$W$为对应层的参数，$b$为对应的偏置量，$\varphi$为相应的激活函数。
RNN中的计算过程多了一个隐藏状态的权重计算：
$H_t=\varphi (X_t{W}_{xh}+H_{t-1}{W}_{hh}+b_h)$，对应的x是一个时间点的信息，$H_{t-1}$为上一时间点的状态信息，$b_h$为对应的偏置量，$\varphi$为相应的激活函数，$W_{xh},W_{hh}$为隐藏层的参数，$b_h$为偏置。
特殊的当为0时，也就是初始时，上一时间点不存在，于是有
$H_0=\varphi (X_0{W}_{xh}+b_h)$

类比输出层的处理为：
$O=H{W}_{hq}+b_q$(全连接)
$O_t=H_t{W}_{hq}+b_q$(RNN)

共享

最终得到一个循环计算：
$\{\begin{array}{l}{H}_0=\varphi (X_0{W}_{xh}+b_h)\\ H_t=\varphi (X_t{W}_{xh}+H_{t-1}{W}_{hh}+b_h)\end{array}$
$O_t=H_t{W}_{hq}+b_q$
这里的参数$W,b$等在不同的时间点都是使用相同的参数，所以其参数的量不会随时间变化增大。这个可以类比在全连接中的参数共享，RNN中的参数共享就是在各个时间点都使用相同的参数，这样对于不同长度的序列其都可以表现出较好的特征提取。

训练

代价函数与全连接相似可以定义为：$L=\frac{1}{T}{\sum }_{t=1}^{T}l(o_t,y_t)$
$l$可以简单的取一下欧式距离或者其他的计算。
之后就是"喜闻乐见"的反向传播，这里叫通过时间反向传播（BPTT）
我们的目标是$W_{hq},W_{xh},W_{hh},b_h,b_q$
链式法则可以得到对应的偏导路径
$\frac{\partial L}{\partial W_{hq}}={\sum }_{t=1}^T\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial W_{hq}}={\sum }_{t=1}^T\frac{\partial L}{\partial o_t}{H}_t^T$

$\frac{\partial L}{\partial b_q}={\sum }_{t=1}^T\frac{\partial L}{\partial o_t}$

$\frac{\partial L}{\partial W_{hx}}={\sum }_{t=1}^T\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial W_{hx}}={\sum }_{t=1}^T\frac{\partial L}{\partial h_t}{x}_t^T$

$\frac{\partial L}{\partial W_{hh}}={\sum }_{t=1}^T\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial W_{hh}}={\sum }_{t=1}^T\frac{\partial L}{\partial h_t}{H}_{t-1}^T$

$\frac{\partial L}{\partial b_h}={\sum }_{t=1}^T\frac{\partial L}{\partial h_t}$

衰减与爆炸

上面的偏导中重复的出现了$\frac{\partial L}{\partial h_t}$，由于循环运算，其偏导的路径不只是$\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial h_t}$，而是：
$\frac{\partial L}{\partial h_t}=\frac{\partial L}{\partial h_{t+1}}\frac{\partial h_{t+1}}{\partial h_t}+\frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial h_t}=W_{hh}^T\frac{\partial L}{\partial h_{t+1}}+W_{qh}^T\frac{\partial L}{\partial o_t}$
这是一个递归式，进一步展开有：
$\frac{\partial L}{\partial h_t}=W_{hh}^T(W_{hh}^T\frac{\partial L}{\partial h_{t+2}}+W_{qh}^T\frac{\partial L}{\partial o_{t+1}})+W_{qh}^T\frac{\partial L}{\partial o_t}$
$\frac{\partial L}{\partial h_t}=W_{hh}^T(W_{hh}^T(W_{hh}^T\frac{\partial L}{\partial h_{t+3}}+W_{qh}^T\frac{\partial L}{\partial o_{t+2}})+W_{qh}^T\frac{\partial L}{\partial o_{t+1}})+W_{qh}^T\frac{\partial L}{\partial o_t}$…

最终得到通式为：$\frac{\partial L}{\partial h_t}={\sum }_{i=t}^T(W_{hh}^T{)}^{T-i}{W}_{qh}^T\frac{\partial L}{\partial o_{T+t-i}}$
当时间步数T较大或者t较小时，多个梯度的乘法很容易产生梯度的爆炸或者消失，对应对$\frac{\partial L}{\partial h_t}$的影响会传播到其他的梯度计算中。

结构

上面的循环神经网络是最常用的，其相应的还有一些其他的结构：

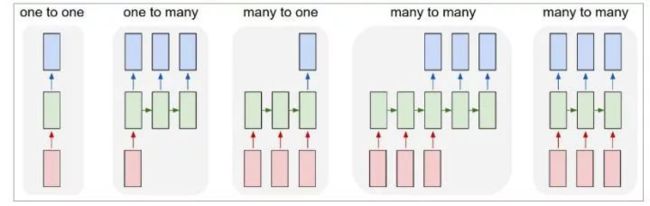
大致的可以了解一下，第一个就是普通的神经网络，第二个是将单一输入来预测输出，也可以拓展到三个时间点都有相同的输入，第三个有点神似于单个的三阶马尔可夫链，对应是一个序列输入到单个输出，第四个是一个有时差的序列转化，第五个就是一个无时差的序列转化。

缺点

从上面的结构中我们可以发现，RNN在理论上是可以存储较长时间前的相关特征，但是在实践实现中，模型中当前时间计算很难获得许久之前时间点的特征，或者说简单的RNN无法获得整个时间区域中有用的上下文信息，太久之前与当前时间点之后的信息都无法学习，虽然可以进行人为参数的挑选，但是在复杂问题上这一处理远远不够，这是简单的RNN在长期记忆中的缺陷。