聚类算法clustering
目录
1、聚类学习定义
2、聚类学习的应用
3、K均值算法(K-means)
(1)地位:
(2)步骤:
(3)程序算法
(4)非可分簇类的应用 编辑
4、优化目标
(1)作用
(2)符号的意思
(3)K均值的优化目标
(4)随机初始化
5、如何选择聚类数量
(1)方法一:观察图
(2)方法二:“肘部法则”(elbow method)
(3)结合你的分类目的(后续目的)作为评价标准
6、数据压缩
(1)作用
(2)降维
(3)降维的作用_可视化化数据
(4)降维的方法_主成分分析法PCA
(5)使用PCA算法对数据降维度
步骤一:进行数据预处理,均值标准化与特征缩放
步骤二:如何找到低维向量或低维平面,如下左图中的u^(1)和右图中的u^(1)和u^(2)
解法如下下图所示
步骤三:如何计算新的低维特征
解法如下
PCA algorithm summary
(6)原始数据的重构
(7)如何选择k,即低维表示z的维度
(8)如何计算得到k
7、PCA的错误应用
(1)不可使用PCA优化过拟合问题
(2)滥用PCA
1、聚类学习定义
无监督学习(无标签,分为几个簇)
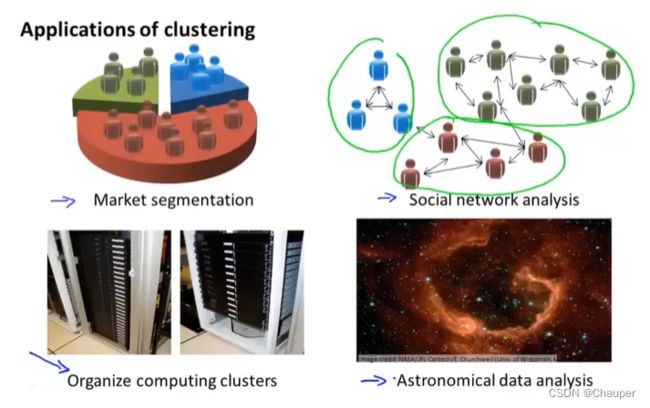
2、聚类学习的应用
3、K均值算法(K-means)
(1)地位:
最热门的、应用最广泛的无监督算法
(2)步骤:
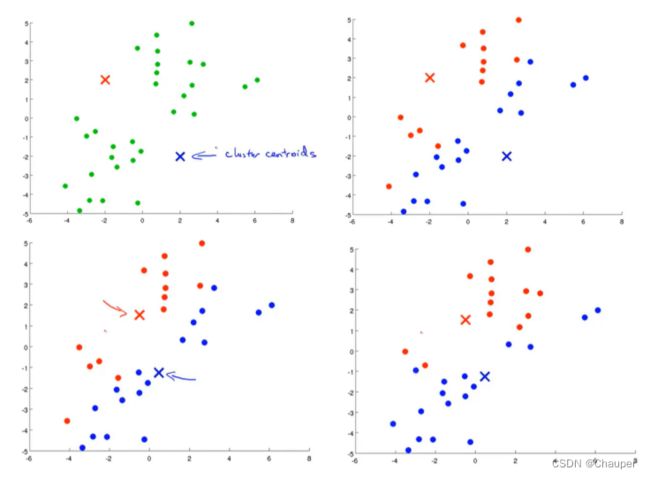
第一步,随机生成两点(即聚类中心)
第二步,迭代算法(簇分配、移动聚类中心)
①首先簇分配,遍历每个数据点,将每个点分配给距离近的聚类中心
②其次移动聚类中心,即移动到同色点的均值处(平均位置)
③再进行一次簇分配,遍历每个数据点,将每个点分配给距离近的聚类中心
④再移动聚类中心……直到所有点都不再变化,此时k均值 已经聚合
(3)程序算法
(4)非可分簇类的应用 
4、优化目标
(1)作用
①确保k均值算法运行正确
②帮助k均值找到更好的簇
(2)符号的意思
c^(i):是当前样本x^(i)所属的那个簇的索引或者序号
μk:是第k个簇类中心的位置(小写的k是聚类中心的下标,大写的K是聚类的个数)
μc^(i):是x^(i)所属的簇类的聚类中心
(3)K均值的优化目标
①函数表达式(失真代价函数):每个样本到所属簇的聚类中心距离的平方值
(如下图点是样本,叉是聚类中心)
(4)随机初始化
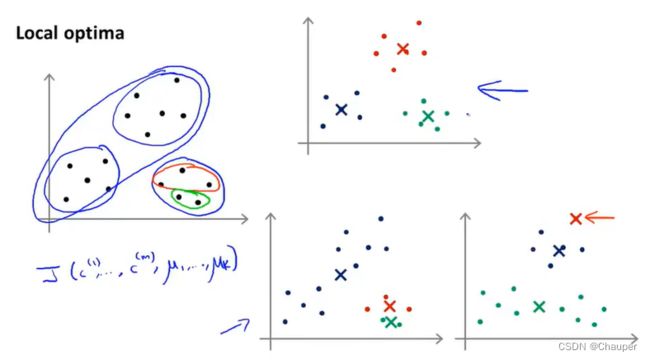
如何初始化聚类中心,几种不同的方法,推荐方法如下:
初始化状态不同,收敛结果不同,k均值可能会落在局部最优,分类结果如下:
解决方法是尝试多次随机初始化,运行多次,具体做法如下:
可选择初始化100次,选取代价最小的一个 ,也就是畸变值最小的
注:k=2-10多次随机初始化可行,若k>10,成百上千个聚类,多次随机初始化不会有太大改善,多的簇类第一次分类效果已经很好,再后来会有改进,不多。但是k较少时,随机初始化影响较大
5、如何选择聚类数量
(1)方法一:观察图
观察可视化的图、观察聚类算法的输出 ,依靠经验
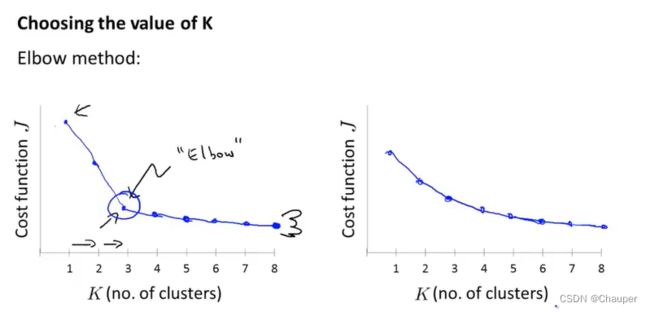
(2)方法二:“肘部法则”(elbow method)
选择拐点处,即肘部处,如下左图所示;此法不常用,因为大部分情况没有一个清晰的拐点,,如下右图所示
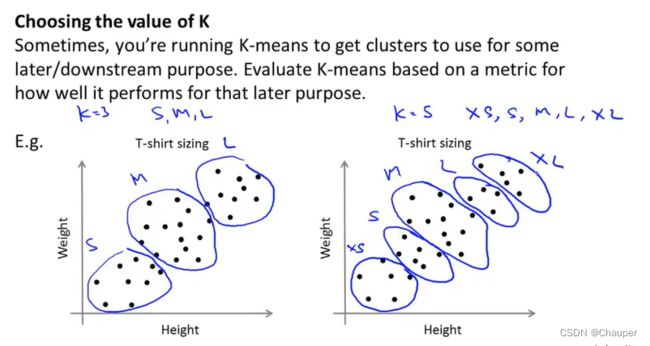
(3)结合你的分类目的(后续目的)作为评价标准
例子如下:
是将T-shirt分为三类S、M、L,还是五类XS、S、M、L、XL,可结合商业角度考虑,是需要更多尺码满足客户,还是更少尺码卖得便宜些;可根据T恤销量来决定k数量
6、数据压缩
(1)作用
①数据进行压缩减少内存
②加快算法计算速度
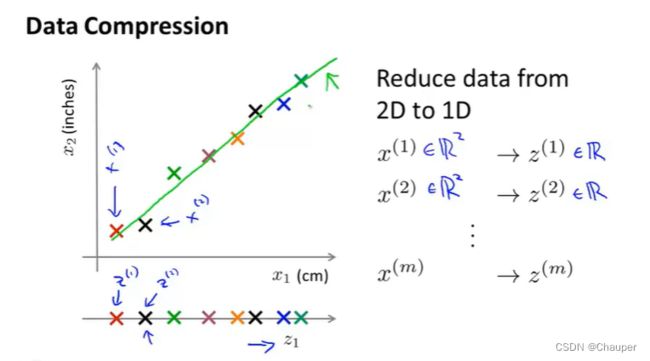
(2)降维
case1:x1和x2是数据集中的两个特征,如下二维图中的点就是两个数来表示,先将绿色的线投影到z1上,使得二维图中的点都可以用一个数来表示0
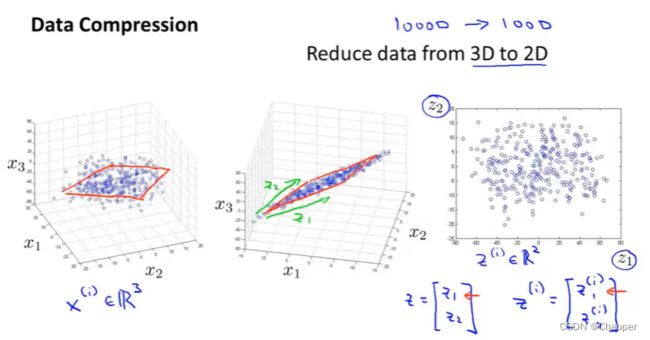
case2:从3D降为到2D,将左图1(绝大部分点落在一个平面)中用三个特征表示的点,最后用两个点表示 ,如图3所示:
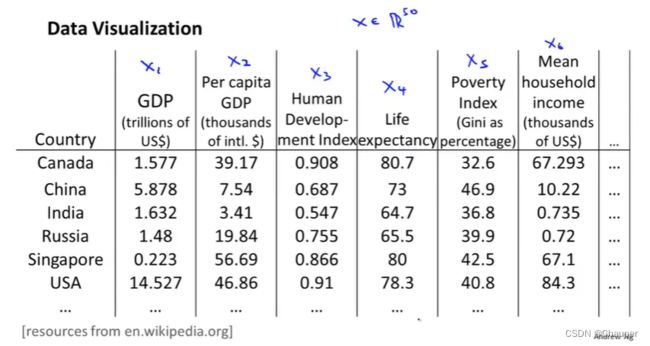
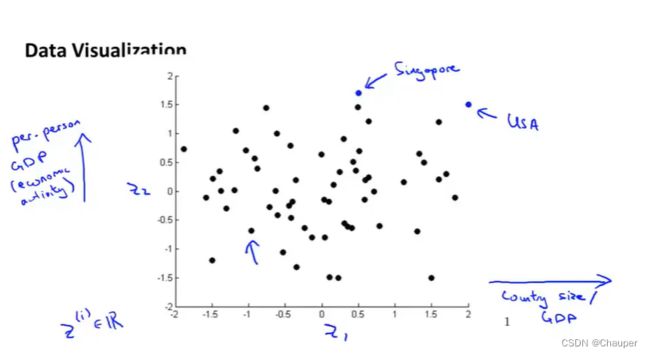
(3)降维的作用_可视化化数据
通过二维图,可便捷地捕捉不同国家两个维度间的变化
(4)降维的方法_主成分分析法PCA
①主成分分析法(principle component analysis)定义
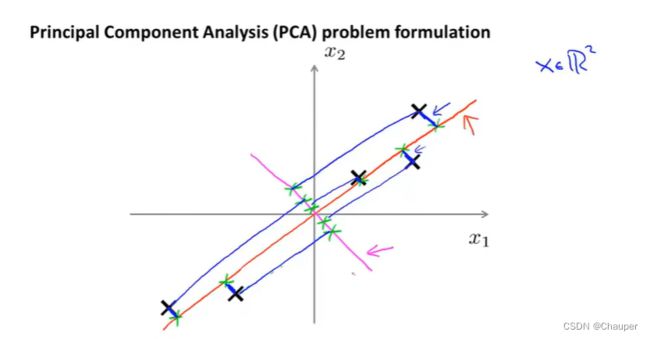
若是从二维降到一维,就是找一个ui∈R^n空间中的向量,即试图寻找一个低维投影平面对数据进行投影,使得投影误差(即每个点与投影后对应点之间距离)的平方(图中蓝色线段)最小化,
例如图中红色线的投影误差远小于粉红色线的误差
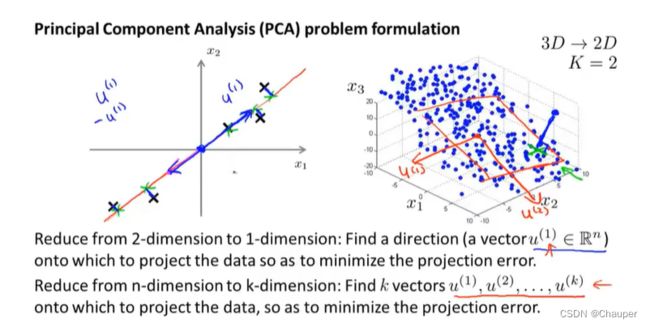
若是降到K维,就不是找两个方向,而是寻找K个方向来对数据进行投影,来最小化投影误差
例子如下,3D降到2D,K=2,就是找出一对向量u^(1)和u^(2),两个向量一起定义了一个二维平面,将这两个向量投影到这两个向量展开的线性子空间上(另一种理解,就是寻找k个方向,寻找k维平面,这里是寻找一个二维平面)
注明:①先进行均值归一化和特征规范化
②PCV和线性回归的区别
区别一:线性回归,拟合一条直线,最小化点和直线的平方误差;PCV是投影误差,如下图所示
区别二:线性回归是用所有的x值来预测y,PCV中同等对待所有x,没有y需要预测
(5)使用PCA算法对数据降维度
步骤一:进行数据预处理,均值标准化与特征缩放
case1:同一特征,一般的标准化,就是先算出均值,再用Xj^(i)- μj替代每一个Xj^(i)
case2:不同的特征不同范围,其中Sj是x的一些测量值,可以是最大值-最小值,或者也可以是一个特征j的标准偏差
保证每个特征都是均值为0的任选特征缩放
步骤二:如何找到低维向量或低维平面,如下左图中的u^(1)和右图中的u^(1)和u^(2)
解法如下下图所示
等号左边是sigma矩阵是 协方差矩阵(n*n的矩阵),等号右边是求和公式,求sigma的特征向量
svd代表奇异值分解,一种高级的分解算法,高级的线性应用(不用了解太深)
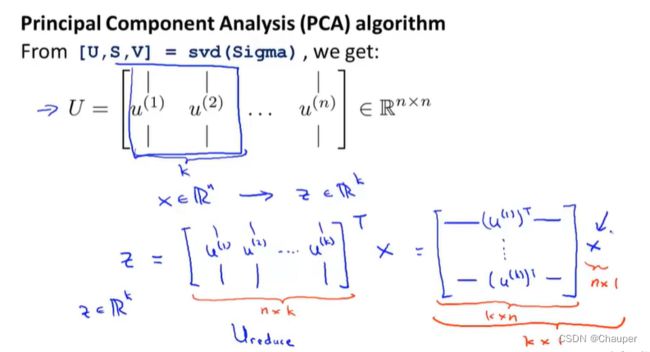
U,S,V是三个矩阵,其中U是n*n的矩阵,U的列就是u^(i)向量,例如是将数据从n维减到k维,则U中取前k个向量
步骤三:如何计算新的低维特征
解法如下
其中x∈R^n,是原始的数据域
PCA algorithm summary
(6)原始数据的重构
即如何从压缩后的低维回到高维,运用矩阵的运算,下图式子成立前提U是正定矩阵,满足条件,因为svd中U*U^T=E
(7)如何选择k,即低维表示z的维度
k也被称为主成分特征含量,主成分的数量,降维后保留的数据量要占到原数据的99%以上
平均投影平方误差÷总方差的商,不超过1%,也就是数据波动,保留99%的差异特性,也就是这里的0.01
(因为希望降维后,这组数据仍然具有很多信息,也就是保持较大的差异性)
(8)如何计算得到k
方法一:左边是从1开始不断递增k,直到公式满足≤0.01,即停止;效率较慢
方法二:右边是svd中S矩阵是一个对角矩阵,左边的公式等于1-对角线kS11加到Skk的和/全部对角线元素求和(这里运用的矩阵知识是奇异值分解),无需像左边那样反复调用svd矩阵,只需调用一次。
7、PCA的错误应用
(1)不可使用PCA优化过拟合问题
原因: PCA损失一部分重要信息,也可能损失一些x与y的对应关心,因为在压缩过程中只关注x,而忽略y;其次过拟合是由于数据中一部分异常数据导致的,而PCA并不一定能剔除数据中的异常数据