PyTorch张量
PyTorch张量
相关基础知识
张量的基本概念
定义:
张量(tensor)是矩阵向任意维度的推广。张量的维度(dimension)通常叫作轴(axis),张量轴的个数也叫作阶(rank)。
概念核心:
张量是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。
应用:
机器学习的数据存储在张量中。一般来说,当前所有机器学习系统都使用张量作为基本数据结构。
张量的关键属性
- 阶:张量的轴的个数。
- 形状:张量沿每个轴的维度大小(元素个数)。在Python中一般用整数元组表示。标量的形状为空元组。
- 数据类型(在Python库中通常叫作dtype):张量中所包含数据的类型。
张量的分类
- 标量(0D 张量):仅包含一个数字的张量叫作标量(scalar)。标量也叫标量张量、零维张量、0D 张量。标量张量有 0 个轴。
- 向量(1D 张量):数字组成的数组叫作向量(vector)或一维张量(1D 张量)。一维张量只有一个轴。
- 矩阵(2D 张量):向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量)。矩阵有 2 个轴(通常叫作行和列)。你可以将矩阵直观地理解为数字组成的矩形网格。第一个轴上的元素叫作行(row),第二个轴上的元素叫作列(column)。
- 3D 张量与更高维张量:将多个矩阵组合成一个新的数组,可以得到一个 3D 张量,你可以将其直观地理解为数字组成的立方体。
易错点提醒:
维度(dimensionality)可以表示沿着某个轴上的元素个数(比如 5D 向量),也可以表示张量中轴的个数(比如 5D 张量),这有时会令人感到混乱。
向量有 5 个元素就被称为 5D 向量。不要把 5D 向量和 5D 张量弄混!对于后一种情况,技术上更准确的说法是 5 阶张量(张量的阶数即轴的个数),但 5D 张量这种模糊的写法更常见。
张量的运算
深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算(tensor operation),例如加上张量、乘以张量等。
你可以将神经网络解释为高维空间中非常复杂的几何变换,这种变换可以通过许多简单的步骤来实现。换句话说就是为复杂的、高度折叠的数据流形找到简洁的表示。这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通过变换使数据解开一点点——许多层堆叠在一起,可以实现非常复杂的解开过程。
逐元素运算(element-wise)
特点:这些运算独立地应用于张量中的每个元素。
例子:relu 运算和加法。
特性:这些运算非常适合大规模并行实现(向量化实现,这一术语来自于 1970—1990 年间向量处理器超级计算机架构)。
广播(broadcast)
应用场景:将两个形状不同的张量相加时,较小的张量会被广播,以匹配较大张量的形状。
步骤
- 向较小的张量添加轴(叫作广播轴),使其 ndim 与较大的张量相同。
- 将较小的张量沿着新轴重复,使其形状与较大的张量相同。
注意事项:在实际的实现过程中并不会创建新的 2D 张量,因为那样做非常低效。重复的操作完全是虚拟的,它只出现在算法中,而没有发生在内存中。
张量积(tensor product)
向量间的点积
两个向量之间的点积是一个标量,而且只有元素个数相同的向量之间才能做点积。
以下代码展示了向量点积运算的步骤,假设x,y均是numpy数组。
def naive_vector_dot(x, y):
"""向量间点积运算简单实现"""
# 判断两个张量是否均为向量
assert len(x.shape) == 1
assert len(y.shape) == 1
# 判断两个向量的维度是否相同
assert x.shape[0] == y.shape[0]
# 初始化一个浮点数,用于存储运算结果
z = 0.
# 将x,y的每个位置的数对应相乘
# 即第一个位置的数和第一个位置的数相乘,以此类推
# 再将所有结果相加
for i in range(x.shape[0]):
z += x[i] * y[i]
return z
矩阵和向量间的点积
一个矩阵 x 和一个向量 y 做点积,返回值是一个向量,其中每个元素是 y 和 x的每一行之间的点积。
def naive_matrix_vector_dot(x, y):
"""矩阵和向量间点积运算简单实现"""
# 初始化一个向量,用于存储运算结果
z = np.zeros(x.shape[0])
# 将x每一行和y做点积运算以后的数作为z的一个数
for i in range(x.shape[0]):
z[i] = naive_vector_dot(x[i, :], y)
return z
任意张量间的点积
注意事项
如果两个张量中有一个的ndim大于 1,那么dot运算就不再是对称的,也就是说,dot(x, y) 不等于 dot(y, x)。
两个矩阵之间的点积
对于两个矩阵 x 和 y,当且仅当 x.shape[1] == y.shape[0] 时,你才可以对它们做点积(dot(x, y))。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵,其元素为 x的行与 y 的列之间的点积。

张量变形(tensor reshaping)
张量变形是指改变张量的行和列,以得到想要的形状。变形后的张量的元素总个数与初始张量相同。
经常遇到的一种特殊的张量变形是转置(transposition)。对矩阵做转置是指将行和列互换,使 x[i, :] 变为 x[:, i]。
张量的应用
向量数据 (samples, features)
意义
这是最常见的机器学习数据集。
编码解释
对于这种数据集,每个数据点都被编码为一个向量,因此一批数据就被编码为 2D 张量。其中第一个轴是样本轴,第二个轴是特征轴。
具体例子
- 人口统计数据集:假设其中包括每个人的年龄、邮编和收入。每个人可以表示为维度为3的向量,而整个数据集包含 100,000 个人,因此可以存储在形状为 (100000, 3) 的 2D张量中。
- 文本文档数据集:若将每个文档表示为每个单词在其中出现的次数(字典中包含20,000 个常见单词)。每个文档可以被编码为包含 20000 个值的向量(每个值对应于字典中每个单词的出现次数),整个数据集包含 500 个文档,因此可以存储在形状为(500, 20000) 的张量中。
序列数据 (samples, timesteps, features)
应用场景
当时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的 3D 张量中。
编码解释
每个样本可以被编码为一个向量序列(即 2D 张量),因此一个数据批量就被编码为一个 3D 张量。根据惯例,时间轴始终是第 2 个轴(索引为 1 的轴)。

具体例子
- 股票价格数据集:如果每一分钟,我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个 3D 向量,整个交易日被编码为一个形状为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),而 250 天的数据则可以保存在一个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
- 推文数据集:我们将每条推文编码为 280 个字符组成的序列,而每个字符又来自于128个字符组成的字母表。在这种情况下,每个字符可以被编码为大小为128的二进制向量(只有在该字符对应的索引位置取值为 1,其他元素都为 0)【词向量概念】。那么每条推文可以被编码为一个形状为 (280, 128) 的2D张量,而包含100万条推文的数据集则可以存储在一个形状为 (1000000, 280, 128) 的张量中。
图像 (samples, height, width, channels) 或 (samples, channels, height, width)
编码解释
图像通常具有三个维度:高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道,因此可以保存在 2D 张量中,但按照惯例,图像张量始终都是 3D 张量,灰度图像的彩色通道只有一维。
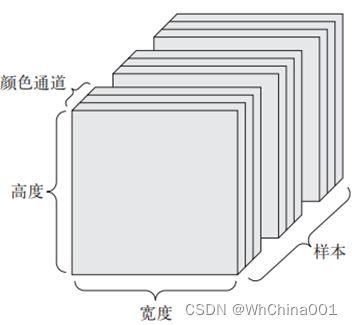
形状约定
图像张量的形状有两种约定:通道在后(channels-last)的约定(在TensorFlow中使用)和通道在前(channels-first)的约定(在Theano中使用)。
视频 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)
意义
视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。
编码解释
视频可以看作一系列帧,每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中,而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为(samples, frames, height, width, color_depth)。
PyTorch张量操作
创建张量
torch.empty(*sizes, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False) → Tensor
作用
创建一个未被初始化数值的tensor,tensor的大小由size确定。
参数解释
- sizes (int):定义输出张量形状的整数序列。 可以是可变数量的参数,也可以是列表或元组之类的集合。
- out (Tensor, optional):输出张量。
- dtype (torch.dtype, optional) :返回张量的所需数据类型。 默认值:如果为None,则使用全局默认值。
- layout (torch.layout, optional):返回的Tensor的所需布局。torch.layout表示torch.Tensor内存布局的对象。有torch.strided(dense Tensors 默认)并为torch.sparse_coo(sparse COO Tensors)提供实验支持。torch.strided代表密集张量,是最常用的内存布局。每个strided张量都会关联 一个torch.Storage,它保存着它的数据。这些张力提供了多维度, 存储的strided视图。Strides是一个整数型列表:k-th stride表示在张量的第k维从一个元素跳转到下一个元素所需的内存。
- device (torch.device, optional):返回张量的所需设备。 默认值:如果为None,则使用当前设备作为默认张量类型。 对于CPU张量类型,设备将是CPU;对于CUDA张量类型,设备将是当前CUDA设备。
- requires_grad (bool, optional):如果autograd应该在返回的张量上记录操作。 默认值:False。因为Pytorch后期的版本将Varibale 和Tensor进行合并了,这里的如果设置为Flase表示再反响传播的时候不会对这个节点机型求导。
- pin_memory (bool, optional):如果设置,返回的张量将在固定的内存中分配。 仅适用于CPU张量。 默认值:False。
torch.rand(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor
作用
返回服从均匀分布的初始化后的tenosr,外形是其参数size。
参数解释
同上。
torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor
作用
返回一个形状为为size,类型为torch.dtype,里面的每一个值都是0的tensor。
参数解释
同上。
拓展
类似的还有torch.ones()。
torch.from_numpy(ndarray) → Tensor
作用
将numpy数组转化为张量。
注意
二者共享内存,对张量进行修改比如重新赋值,那么原始数组也会相应发生改变。
torch.tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False) → Tensor
作用
根据输入的数据生成一个张量。
参数解释
- data(list or tuple or numpy.ndarray so on.):将指定的可迭代对象转换为张量。
- dtype(torch.dtype, optional):该参数可选参数,默认为None。如果不进行设置,生成的Tensor数据类型会拷贝data中传入的参数的数据类型,比如data中的数据类型为float,则默认会生成数据类型为torch.FloatTensor的Tensor。
- device (torch.device, optional):同上。
- requires_grad (bool, optional):同上。
- pin_memory (bool, optional):同上。
注意
- torch.Tensor为Python的一个类,且是默认张量类型torch.FloatTensor()的别名。
- torch.tensor为Python的一个函数,而且可以根据原始数据类型自动选择相应类型的张量,而不仅仅是单精度浮点型张量。
获取张量信息
size() → torch.Size
作用
获取当前张量的形状。
返回值
tuple的一个子类。
item()
只有单个元素的张量,获取该元素用该方法。
改变张量
切片
类似于Python自身的切片,“[]”符号可以是小于张量维度数的任意个表达式。可以间隔取数。
view() → Tensor
用法解释
- 直接指定形状:x.view(1,1,6)
- torch.view(-1):将张量推平成一维的。
- 自动计算形状,不想算的位置放上-1,以下写法等效:x.view(4,5),x.view(-1,5),x.view(4,-1)。
注意
view()返回的tensor和传入的tensor共享内存。意思就是修改其中一个,数据都会变。
cuda() → Tensor
用法解释
将Tensor转到GPU上。
张量相互间操作
加法
主要有以下几种方法。
- 直接使用Python操作符:+
- 调用pytorch库内的加法函数:torch.add(x, y, out=),out是可选参数,即是否将结果存放于指定张量中,该张量一般用torch.empty()创建。
- 调用张量自身的加法函数:x.add_(y)(这会使张量x发生变化,返回改变以后的x)
- 调用张量自身的加法函数:x.add(y)(这不会使张量x发生变化,返回一个全新的Tensor)