08-SVM支持向量机(SVC)
1.1 原理简介
支持向量机(support vector machines,SVM)是一种二分类算法,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,如果对应的样本特征少,一个普通的SVM就是一条线将样本分隔开,但是要求线到两个类别最近样本点的距离要最大。
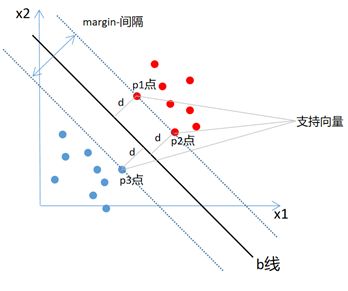
就是在寻找一个最优的决策边界(上图中的两条虚线)来确定分类线b,所说的支持向量(support vector)就是距离决策边界最近的点(上图中p1、p2、p3点,只不过边界穿过了这些点)。如果没有这些支持向量点,b线的位置就要改变,所以SVM就是根据这些支持向量点来最大化margin,来找到了最优的分类线(machine,分类器),这也是SVM分类算法名称的由来。
1.2 构建SVM目标函数
接着上面的分类问题来分析,假设支持向量机最终要找的线是 l 2 l_2 l2,决策边界两条线是 l 1 l_1 l1和 l 3 l_3 l3,那么假设 l 2 l_2 l2的方程为 w T ⋅ x + b = 0 w^T⋅x+b=0 wT⋅x+b=0,这里w表示 ( w 1 , w 2 ) T (w_1,w_2 )^T (w1,w2)T,x表示 ( x 1 , x 2 ) T (x_1,x_2 )^T (x1,x2)T,我们想要确定 l 2 l_2 l2直线,只需要确定w和b即可,此外,由于 l 1 l_1 l1和 l 3 l_3 l3线是 l 2 4 l_24 l24的决策分类边界线,一定与 l 2 l_2 l2是平行的,平行就意味着斜率不变,b变化即可,所以我们可以假设l_1线的方程为 w T ⋅ x + b = c w^T⋅x+b=c wT⋅x+b=c,l_3线的方程为 w T ⋅ x + b = − c w^T⋅x+b=-c wT⋅x+b=−c。
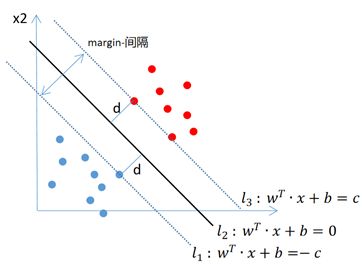
二维空间点 ( x 1 , y 1 ) (x_1,y_1 ) (x1,y1)到直线 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0的距离公式为:
d = ∣ A x 1 + B y 1 + C ∣ ( A 2 + B 2 ) d=\frac{|Ax_1+By_1+C|}{\sqrt{(A^2+B^2 )}} d=(A2+B2)∣Ax1+By1+C∣
我们希望的是决策边界上的样本点到 l 2 l_2 l2直线的距离d越大越好。我们可以直接计算 l 1 l_1 l1 或 l 3 l_3 l3上的点到直线 l 2 l_2 l2的距离,假设将空间点扩展到n维空间后,点 x i = ( x 1 , x 2 . . . x n ) x_i=(x_1,x_2...x_n ) xi=(x1,x2...xn)到直线 w T ⋅ x + b = 0 w^T⋅x+b=0 wT⋅x+b=0(严格意义上来说直线变成了超平面)的距离为:
d = ∣ w T ⋅ x i + b ∣ ‖ w ‖ d=\frac{|w^T⋅x_i+b|}{‖w‖} d=‖w‖∣wT⋅xi+b∣
以上 ‖ w ‖ = ( w 1 2 + w 2 2 + . . . + w n 2 ) ‖w‖=\sqrt{(w_1^2+w_2^2+...+w_n^2 )} ‖w‖=(w12+w22+...+wn2),读做“w的模”。
1.3 拉格朗日乘数法、KKT条件、对偶(扩展)
1.3.1 拉格朗日乘数法
拉格朗日乘数法主要是将有等式约束条件优化问题转换为无约束优化问题,拉格朗日乘数法如下:
假设 x = [ x 1 , x 2 , . . . , x n ] x=[x_1,x_2,...,x_n ] x=[x1,x2,...,xn]是一个n维向量, f ( x ) f(x) f(x)和 h ( x ) h(x) h(x)含有x的函数,我们需要找到满足 h ( x ) = 0 h(x)=0 h(x)=0条件下 f ( x ) f(x) f(x)最小值,如下:
L ( x , λ ) = f ( x ) + λ h ( x ) L(x,λ)=f(x)+λh(x) L(x,λ)=f(x)+λh(x)
拉格朗日函数转换成等式过程的证明涉及到导数积分等数学知识,参考文章:
https://blog.csdn.net/Soft_Po/article/details/118332454
1.3.2 KKT条件
假设 x = [ x 1 , x 2 , . . . , x n ] x=[x_1,x_2,...,x_n ] x=[x1,x2,...,xn]是一个n维向量, f ( x ) f(x) f(x)和 h ( x ) h(x) h(x)含有x的函数,我们需要找到满足 h ( x ) ≤ 0 h(x)≤0 h(x)≤0条件下 f ( x ) f(x) f(x)最小值,我们可以考虑加入一个“松弛变量” a 2 a^2 a2让条件 h ( x ) h(x) h(x)≤ 0来达到等式的效果,即使条件变成 h ( x ) + a 2 = 0 h(x)+a^2=0 h(x)+a2=0,这里加上 a 2 a^2 a2的原因是保证加的一定是非负数,即: a 2 ≥ 0 a^2≥0 a2≥0,但是目前不知道这个 a 2 a^2 a2值是多少,一定会找到一个合适的 a 2 a^2 a2值使 h ( x ) + a 2 = 0 h(x)+a^2=0 h(x)+a2=0成立。
通过转换:
L ( x , λ , a ) = f ( x ) + λ ( h ( x ) + a 2 ) L(x,λ,a)=f(x)+λ(h(x)+a^2 ) L(x,λ,a)=f(x)+λ(h(x)+a2)
但是上式中λ值必须满足λ≥0,由于 L ( x , λ , a ) L(x,λ,a) L(x,λ,a)变成了有条件的拉格朗日函数,这里需要求 m i n L ( x , λ , a ) minL(x,λ,a) minL(x,λ,a)对应下的x值。
{ ∂ L / ∂ x = ( ∂ f ( x ) ) / ∂ x + λ ⋅ ( ∂ h ( x ) ) / ∂ x = 0 h ( x ) ≤ 0 λ ⋅ h ( x ) = 0 λ ≥ 0 \left\{ \begin{array}{c} ∂L/∂x=(∂f(x))/∂x+λ⋅(∂h(x))/∂x=0 \\ h(x)≤0 \\ λ⋅h(x)=0 \\ λ≥0 \end{array}\right. ⎩ ⎨ ⎧∂L/∂x=(∂f(x))/∂x+λ⋅(∂h(x))/∂x=0h(x)≤0λ⋅h(x)=0λ≥0 以上便是不等式约束优化问题的KKT(Karush-Kuhn-Tucker)条件,我们回到最开始要处理的问题上,根据③式可知,我们需要找到合适的x,λ,a值使L(x,λ,a)最小,但是合适的x,λ,a必须满足KKT条件。
1.3.3 对偶问题
对偶问题是我们定义的一种问题,对于一个不等式约束的原问题, 我们定义对偶问题为(对上面方程的求解等效求解下面方程),其实就是把min和max对调了一下,当然对应的变量也要变换。
1.4 最小化SVM目标函数
通过推导我们知道SVM目标函数如下, 根据拉格朗日乘数法、KKT条件、对偶问题我们可以按照如下步骤来计算SVM目标函数最优的一组w值。
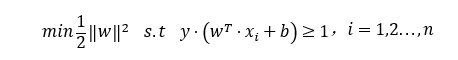
1.4.1 构造拉格朗日函数
将SVM目标函数转换为如下:
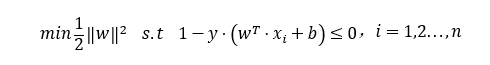
以上不等式转换成拉格朗日函数必须满足KKT条件:

1.4.2 对偶转换
由于原始目标函数 1 / 2 ‖ w ‖ 2 1/2 ‖w‖^2 1/2‖w‖2是个下凸函数,根据1.3.3中对偶问题可知 L ( w , b , λ ) L(w,b,λ) L(w,b,λ)一定是强对偶问题,所以可以将a式改写成如下:
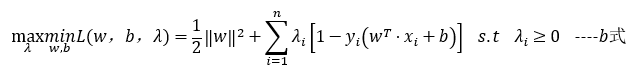
1.4.3 SMO算法求解
SMO(Sequential Minimal Optimization),序列最小优化算法,其核心思想非常简单:每次只优化一个参数,其他参数先固定住,仅求当前这个优化参数的极值。
1.4.4 计算分割线w和b的值
我们可以知道获取了一组λ的值,我们可以得到一组w对应的值。假设我们有S个支持向量,以上b的计算可以使用任意一个支持向量代入计算即可,如果数据严格是线性可分的,这些b结果是一致的。
对于数据不是严格线性可分的情况,参照后面的软间隔问题,一般我们可以采用一种更健壮的方式,将所有支持向量对应的b都求出,然后将其平均值作为最后的结果,最终求出b的结果。
确定w和b之后,我们就能构造出最大分割超平面:w^T⋅x+b=0,新来样本对应的特征代入后得到的结果如果是大于0那么属于一类,小于0属于另一类。
1.5 软间隔及优化
1.5.1 软间隔问题
以上讨论问题都是基于样本点完全的线性可分,我们称为硬间隔。如果存在部分样本点不能完全线性可分,那么我们就需要用到软间隔,相比于硬间隔的苛刻条件,我们允许个别样本点出现在间隔带里面, 即我们允许部分样本点不满足约束条件。
为了度量这个间隔软到何种程度,我们为每个样本引入一个“松弛变量” ξ i , ξ i ≥ 0 ξ_i,ξ_i≥0 ξi,ξi≥0,(中文:克西)加入松弛变量后,我们的约束条件变成 y ⋅ ( w T ⋅ x i + b ) ≥ 1 − ξ i y⋅(w^T⋅x_i+b)≥1-ξ_i y⋅(wT⋅xi+b)≥1−ξi,这样不等式就不会那么严格。
1.5.2 优化SVM目标函数
加入软间隔后我们的目标函数变成了:

其中C是一个大于0的常数,当C为无穷大, ξ i ξ_i ξi必然无穷小,这样的话SVM就变成一个完全线性可分的SVM。如果C为有对应的值时, ξ i ξ_i ξi对应的会有一个大于0的值,这样的SVM就是允许部分样本不遵守约束条件,接下来我们对新的目标函数h式求解最优化问题。
1.5.3 SVM代码
from sklearn import svm
import numpy as np
def read_data(path):
with open(path) as f :
lines=f.readlines()
lines=[eval(line.strip()) for line in lines]
X,y=zip(*lines)
X=np.array(X)
y=np.array(y)
return X,y
if __name__ == '__main__':
X_train,y_train=read_data("./data/train_data")
X_test,y_test=read_data("./data/test_data")
#C对样本错误的容忍,这里就是SVM中加入松弛变量对应的C,
model= svm.SVC(C=1.0)
model.fit(X_train,y_train.ravel())
#打印支持向量
print(model.support_vectors_)
#打印支持向量下标
print(model.support_)
#使用SVM应用到测试集,返回正确率
score = model.score(X_test,y_test)
print(score)
1.5.4 网格搜索
网格搜索就是手动给定模型中想要改动的所有参数,程序自动使用穷举法来将所有的参数或者参数组合都运行一遍,将对应得到的模型做K折交叉验证,将得分最高的参数或参数组合当做最佳结果,并得到模型。也就是说网格搜索用来获取最合适的一组参数,不需要我们手动一个个尝试。
使用网格搜索由于针对每个参数下的模型需要做K折交叉验证最终导致加大了模型训练时间,所以一般我们可以在小的训练集中使用网格搜索找到对应合适的参数值,再将合适的参数使用到大量数据集中训练模型。例如:逻辑回归中使用正则项时,我们可以先用一小部分训练集确定合适的惩罚系数,然后将惩罚系数应用到大量训练集中训练模型。
1.6 SVM Hinge Loss 损失函数
其实这里我们说SVM的损失主要说的就是上式中的松弛变量 ξ i ξ_i ξi损失,当所有样本总的 ξ i ξ_i ξi为0时那么就是一个完全线性可分的SVM;如果SVM不是线性可分,那么我们希望总体样本的松弛变量越小越好。
1.7 核函数
1.7.1 非线性SVM
在前面SVM讨论的硬间隔和软间隔都是指的样本完全可分或者大部分样本点线性可分的情况。我们可以使用升维方式来解决这种线性不可分的问题,例如目前只有两个维度 x 1 x_1 x1 、 x 2 x_2 x2,我们可以基于已有的维度进行升维得到更多维度,例如: x 1 x 1 、 x 1 x 2 、 x 2 x 2 x_1 x_1 、x_1 x_2 、x_2 x_2 x1x1、x1x2、x2x2,这样我们可以将以上问题可以转换成高维可分问题。
1.7.2 核函数(Kernel Function)
假设原有特征有如下三个 x 1 、 x 2 、 x 3 x_1 、x_2 、x_3 x1、x2、x3,那么基于三个已有特征进行两两组合(二阶交叉)我们可以得到如下更多特征,
[ x 1 x 1 、 x 1 x 2 、 x 1 x 3 、 x 2 x 1 、 x 2 x 2 、 x 2 x 3 、 x 3 x 1 、 x 3 x 2 、 x 3 x 3 ] [x_1 x_1 、x_1 x_2 、x_1 x_3 、x_2 x_1 、x_2 x_2 、x_2 x_3 、x_3 x_1 、x_3 x_2 、x_3 x_3 ] [x1x1、x1x2、x1x3、x2x1、x2x2、x2x3、x3x1、x3x2、x3x3]
我们在训练模型时将以上组合特征可以参与到模型的训练中,其代价是运算量过大,比如原始特征有m个,那么二阶交叉的维度为 C m 2 C_m^2 Cm2个,这种量级在实际应用中很难实现,那么有没有一种方式可以在升维的同时可以有效的降低运算量,在非线性SVM中,核函数就可以实现在升维的同时可以有效降低运算量。
以上核函数叫做多项式核函数,常用的核函数有如下几种,不同的核函数的区别是将向量映射到高维空间时采用的升维方法不同,不过高维向量都是不需要计算出来的。
线性核函数:
K ( x i ⋅ x j ) = x i T ⋅ x j K(x_i⋅x_j )={x_i}^T⋅x_j K(xi⋅xj)=xiT⋅xj
多项式核函数:
K ( x i ⋅ x j ) = ( α ( x i T ⋅ x j ) + c ) d K(x_i⋅x_j )=(α({x_i}^T⋅x_j )+c)^d K(xi⋅xj)=(α(xiT⋅xj)+c)d (α,c,d都是参数)
高斯核函数:
K ( x i ⋅ x j ) = K(x_i⋅x_j )= K(xi⋅xj)= e − ‖ x i − x j ‖ 2 2 δ 2 e^{-\frac{{‖x_i-x_j‖}^2}{2δ^2}} e−2δ2‖xi−xj‖2 ( δ δ δ是参数)
1.7.3 核函数在SVM中的应用
在非线性SVM中,我们可以对原始特征进行升维,原有的超平面 w T ⋅ x + b = 0 w^T⋅x+b=0 wT⋅x+b=0变成了 w T ⋅ φ x + b = 0 w^T⋅φx+b=0 wT⋅φx+b=0,然后经过对偶处理目标函数,
这样我们可以通过核函数将数据映射到高维空间,但是核函数是在低维上进行计算,而将实质上的分类效果表现在了高维空间上,来解决在原始空间中线性不可分的问题。
在SVM中我们可以使用常用的核函数:线性核函数、多项式核函数、高斯核函数来进行升维解决线性不可分问题,应用最广泛的就是高斯核函数,无论是小样本还是大样本、高维或者低维,高斯核函数均适用,它相比于线性核函数来说,线性核函数只是高斯核函数的一个特例,线性核函数适用于数据本身线性可分,通过线性核函数来达到更理想情况。
高斯核函数相比于多项式核函数,多项式核函数阶数比较高时,内部计算时会导致一些元素值无穷大或者无穷小,而在高斯核函数会减少数值的计算困难。
综上,我们在非线性SVM中使用核函数时,先使用线性核函数,如果不行尝试换不同的特征,如果还不行那么可以直接使用高斯核函数。
from sklearn import svm
from sklearn import datasets
from sklearn.model_selection import train_test_split as ts
'''
‘rbf’:高斯核函数
‘linear’:线性核函数
‘poly’:多项式核函数
'''
if __name__ == '__main__':
#import our data
iris = datasets.load_iris()
X = iris.data
y = iris.target
#split the data to 7:3
X_train,X_test,y_train,y_test = ts(X,y,test_size=0.3)
print(y_test)
# select different type of kernel function and compare the score
# kernel = 'rbf'
clf_rbf = svm.SVC(kernel='rbf')
clf_rbf.fit(X_train,y_train)
score_rbf = clf_rbf.score(X_test,y_test)
print("The score of rbf is : %f"%score_rbf)
# kernel = 'linear'
clf_linear = svm.SVC(kernel='linear')
clf_linear.fit(X_train,y_train)
score_linear = clf_linear.score(X_test,y_test)
print("The score of linear is : %f"%score_linear)
# kernel = 'poly'
clf_poly = svm.SVC(kernel='poly')
clf_poly.fit(X_train,y_train)
score_poly = clf_poly.score(X_test,y_test)
print("The score of poly is : %f"%score_poly)
1.8 支持向量机SVM特点
1.8.1 抗干扰能力强
根据一些样本点,我们可以通过拉格朗日乘数法、KKT条件、对偶问题、SMO算法计算出支持向量机SVM的分类线 w T ⋅ x + b = 0 w^T⋅x+b=0 wT⋅x+b=0。
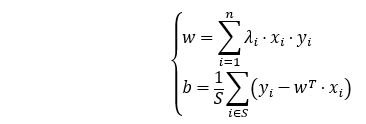 (代表的是边界上的样本点)
(代表的是边界上的样本点)
我们可以看出SVM在训练过程中找到的是两类点的分割线,计算样本中有少量异常点,在训练模型时依然能很正确的找到中间分割线,因为训练SVM时考虑了全量数据,确定这条线的b时只与支持向量点(边界上的点)有关。同样在测试集中就算有一些样本点是异常点也不会影响其正常分类,SVM具有抗干扰能力强的特点。
此外,由于训练SVM需要所有样本点参与模型训练,不然不能缺点这条线,所以当数据量大时,SVM训练占用内存非常大。这时SVM模型的缺点。
1.8.2 二分类及多分类
SVM同样支持多分类,我们可以将一个多分类问题拆分成多个二分类问题,例如有A,B,C三类,我们使用SVM训练时可以训练3个模型,第一个模型针对是A类和不是A类进行训练。第二个模型针对是B类和不是B类进行训练。第三个模型针对是C类和不是C类进行训练。这样可以解决多分类问题。