机器学习:Kernel PCA核主成分分析
1. kernel PCA 概述
核主成分分析(Kernelized PCA,KPCA)利用核技巧将d维线性不可分的输入空间映射到线性可分的高维特征空间中,然后对特征空间进行PCA降维,将维度降到d′ 维,并利用核技巧简化计算。也就是一个**先升维后降维【数据先通过核函数(kernel function)转换成一个新空间,也就是升维过程,然后再用PCA进行降维处理】**的过程,这里的维度满足d′
线性降维方法假设从高维空间到低维空间的函数映射是线性的,然而在有些时候,高维空间是线性不可分的,需要找到一个非线性函数映射才能进行恰当的降维,这就是非线性降维。
KPCA就是一种非线性降维方法
2. KPCA的实施步骤
以 Radial Basis Function(RBF) kernel PCA(不同的核,体现在代码上仅仅是一处细微的差别)为例进行说明:
- 计算核矩阵***K***【相似度矩阵】

这是最为常见的RBF(Rational Basis Function)核函数,也有多项式核:

和sigmoid型(hyperbolic tangent)核:

其矩阵形式也即:

- center the K
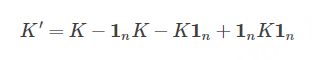
其中 1n是 n×n 的元素值全为1/n矩阵 - 对 K′进行特征值分解,获得对应于前 k个特征值的特征向量。与标准PCA算法不同的是,这里获得特征向量不再是 principal component axes,而已经是全部样本在这些轴上的投影了,也即是我们所需的进行降维后的数据了。
3. Python实现KPCA与PCA
3.1 Case1:
import numpy as np
import matplotlib.pyplot as plt
#构建样本数据
A1_mean = [1, 1]
A1_cov = [[2, .99], [1, 1]]
A1 = np.random.multivariate_normal(A1_mean, A1_cov, 50)
A2_mean = [5, 5]
A2_cov = [[2, .99], [1, 1]]
A2 = np.random.multivariate_normal(A2_mean, A2_cov, 50)
A = np.vstack((A1, A2))
B_mean = [5, 0]
B_cov = [[.5, -1], [.9, -.5]]
B = np.random.multivariate_normal(B_mean, B_cov, 100)
f = plt.figure(figsize=(10, 10))
ax = f.add_subplot(111)
ax.set_title("$A$ and $B$ processes")
ax.scatter(A[:, 0], A[:, 1], color='r')
ax.scatter(A2[:, 0], A2[:, 1], color='r')
ax.scatter(B[:, 0], B[:, 1], color='b')
#KPCA处理结果
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel='cosine', n_components=1)
AB = np.vstack((A, B))
AB_transformed = kpca.fit_transform(AB)
A_color = np.array(['r']*len(B))
B_color = np.array(['b']*len(B))
colors = np.hstack((A_color, B_color))
f = plt.figure(figsize=(10, 4))
ax = f.add_subplot(111)
ax.set_title("Cosine KPCA 1 Dimension")
ax.scatter(AB_transformed, np.zeros_like(AB_transformed), color=colors)
#PCA处理结果
from sklearn.decomposition import PCA
pca = PCA(1)
AB_transformed_Reg = pca.fit_transform(AB)
f = plt.figure(figsize=(10, 4))
ax = f.add_subplot(111)
ax.set_title("PCA 1 Dimension")
ax.scatter(AB_transformed_Reg, np.zeros_like(AB_transformed_Reg), color=colors)
构建的样本数据散点图如下:

KPCA处理后的结果如下:
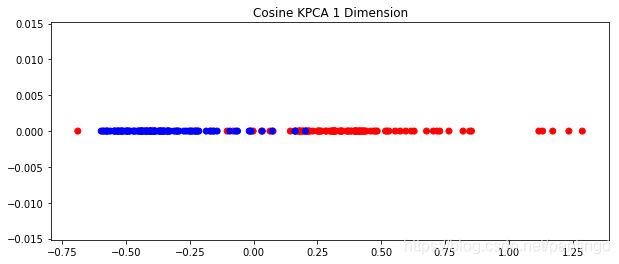
PCA处理的结果如下:

从上述三张图片可以看出,针对非线性数据降维,KPCA的降维效果优于PCA方法
3.2 Case2:
样本数据散点图如下:
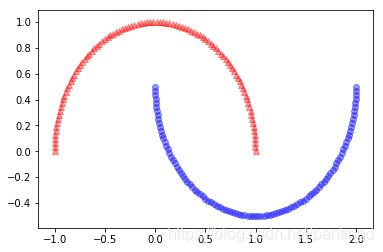
将样本数据升维又降维处理后的结果如下图:

具体实现代码
#构建样本数据
from sklearn.datasets import make_moons
from scipy.spatial.distance import pdist, squareform
X, y = make_moons(n_samples=200, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], color='r', marker='^', alpha=.4)
plt.scatter(X[y==1, 0], X[y==1, 1], color='b', marker='o', alpha=.4)
#KPCA处理结果
def rbf_kpca(X, gamma, k):
sq_dist = pdist(X, metric='sqeuclidean')
# N = X.shape[0]
# sq_dist.shape = N*(N-1)/2
mat_sq_dist = squareform(sq_dist)
# mat_sq_dist.shape = (N, N)
# step 1
K = np.exp(-gamma*mat_sq_dist)
# step 2
N = X.shape[0]
one_N = np.ones((N, N))/N
K = K - one_N.dot(K) - K.dot(one_N) + one_N.dot(K).dot(one_N)
# step 3
Lambda, Q = np.linalg.eig(K)
eigen_pairs = [(Lambda[i], Q[:, i]) for i in range(len(Lambda))]
eigen_pairs = sorted(eigen_pairs, reverse=True, key=lambda k: k[0])
return np.column_stack((eigen_pairs[i][1] for i in range(k)))
#调用上述自定义函数
X_kpca = rbf_kpca(X, gamma=15, k=2)
#将降维处理后的数据绘制出来
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1], color='r', marker='^', alpha=.4)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1], color='b', marker='o', alpha=.4)
label_count = np.bincount(y)
# 统计各类别出现的次数
# label_count[0] = 500
# label_count[1] = 500
ax[1].scatter(X_kpca[y==0, 0], np.zeros(label_count[0]), color='r')
ax[1].scatter(X_kpca[y==1, 0], np.zeros(label_count[1]), color='b')
# y轴置零
# 投影到x轴
ax[1].set_ylim([-1, 1])
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_xlabel('PC1')
plt.show()
注:核函数处理非线性分离效果很好,但是一不小心就可能导致拟合过度。
参考文献:
1. http://blog.csdn.net/u013719780
2. https://blog.csdn.net/lanchunhui/article/details/50492482