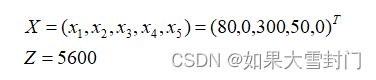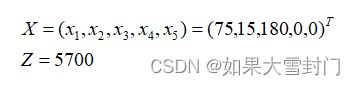python最优化算法实战---线性规划之单纯形法
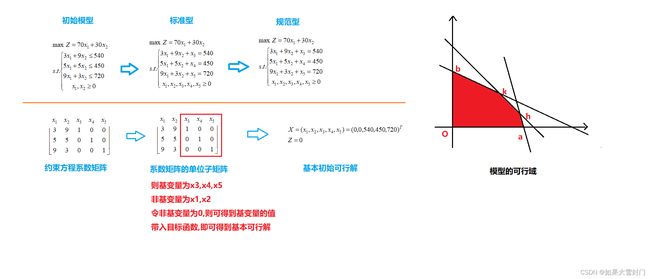
1.线性规划的标准型
在线性规划求解的方法中,模型的标准形式需要满足一下几个条件:
(1)目标函数求最大值
(2)约束条件为等式约束
(3)约束条件右边的常数项大于或等于0
(4)所有变量大于或等于0
对于非标准形式的模型,约束方程可以通过引入松弛变量使不等式约束转换为等式约束,如下所示,将一个非标准形式的模型转化为标准形式的模型。
2.单纯形法
2.1单纯形法的原理
线性规划模型中目标函数和约束方程都是凸函数,从凸优化的角度来讲,线性规划的最优解在可行域的顶点上,单纯形法的本质就是通过矩阵的线性变化来遍历这些顶点以计算最优解。
1.什么是凸集合?
假设有一个集合s,如果该集合中的任意两个顶点以及连接这两个顶点的线段都属于s集合,则集合s被称为凸集。如下图所示,图左边为非凸集,右边为凸集。
2.什么是凸函数?
定义在凸集上的函数被称为凸函数。(这就是为什么目标函数和约束方程都是凸函数的原因)
2.2单纯形法的求解过程
2.2.1 规范型
要用单纯型法求解线性规划数学模型,还需要把模型转换为规范型,而规范型需要满足以下条件。
(1)数学模型已是标准型
(2)约束方程组系数矩阵中含有至少一个单位子矩阵,对应的变量成为基变量,基的作用是得到初始基本可行解。
(3)目标函数中不含基变量
2.2.2 单纯形法的具体计算过程
1.确定基本初始可行解
利用规范型的数学模型,整理出目标函数和约束方程的形式。(我们以最初的模型为例子)
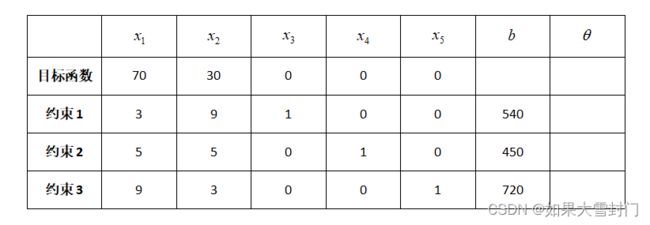
此时顶点的位置是原点,初始的单纯型表如下所示。
2.判断当前点X是否是最优解
对于最大化问题,若当前目标函数中的非基变量的系数小于等于0时,则所得的解为最优解。而在当前的例子中,非基变量的系数分别为70和30,意味着在可行域内随着非基变量x1和x2的增大,目标函数就会继续增大,因此当前的解不是最优解。故判断当前所得的解是否为最优解时,只需判断目标函数中非基变量的系数是否小于等于0。
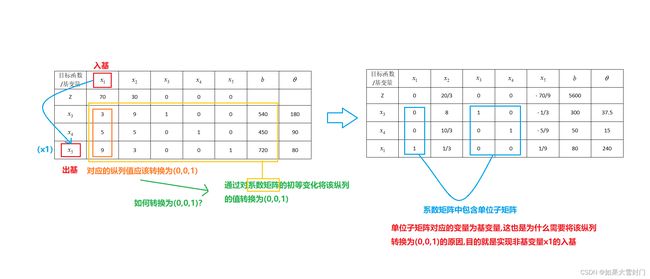
3.基变量出基与非基变量入基
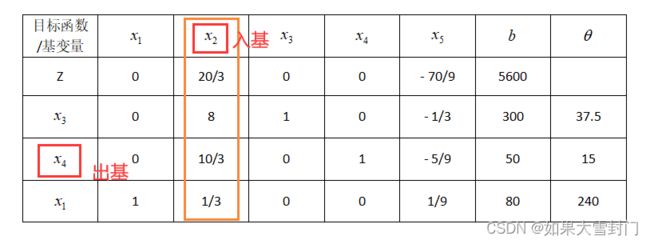
变量的出基与入基,在几何图像上表现为顶点的变化。入基的规则为选择使目标函数z变化最快的非基变量入基,即选择系数最大且为正数的非基变量入基,故在本例中选择x1入基。出基的规则则需要引入一个新的量θ,θ=b/ai(ai为非基变量系数,ai的选择的是刚刚入基的非基变量的系数),选择最小的θ出基。
如上表所示,选择基变量x5出基。
第一次迭代,经过x1入基与x5出基的运算后,得到的结果如下所示。
令非基变量的值为0,则得到第一次迭代的解,如下所示
判断该解是否为最优解(重复第二个步骤,直到是最优解为止),显然由于非基变量x2的系数大于0,故当前位置还不是最优解,再次重复步骤3。
1.非基变量如何入基?
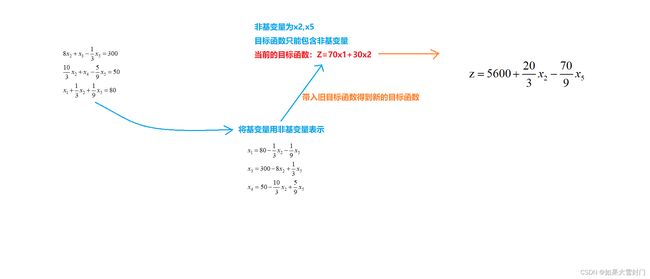
我们以上述例子示范,第一次迭代时,当判断x1入基,x5出基时,找到表中x1和x5对应的列,将x5替换为x1,然后将这一纵列的值转换为(0,0,1),具体过程如下图所示。
2.如何更新目标函数?
当我们完成非基变量的入基后,可以得到跌倒后的约束条件,同样以上述例子来讲解,具体过程如下图所示。
实际上,我们同样可以使用矩阵的初等变化来得到相对于的目标函数。
同样的方法,可以看出x2入基,列出出基计算表。
可以看出x4对应的θ最小,所以选择x4出基。
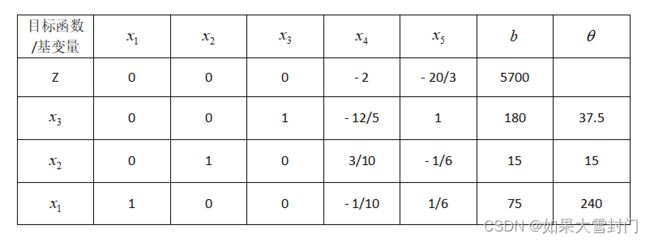
第二次迭代,x2入基,x4出基,得到的结果如下表所示。
得到当前的可行解为
判断该解是否为最优解,由于非基变量在目标函数中的系数均小于0,所以该解即为当前模型的最优解。
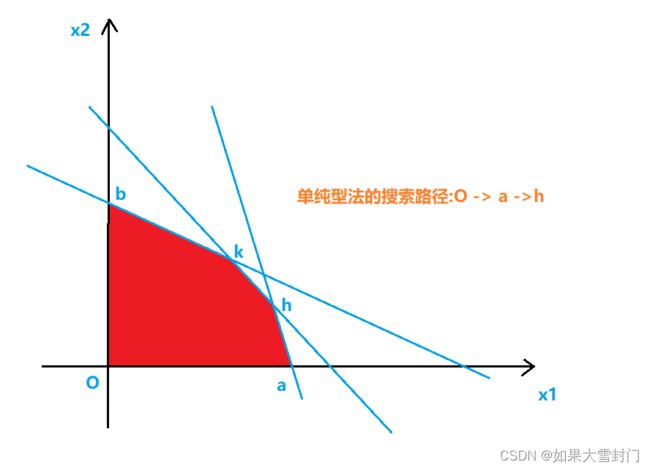
单纯法的搜索路径如下图所示。
3.单纯型法代码
import pandas as pd
import numpy as np
"""
系数矩阵的形式:
b x1 x2 x3 x4 x5
obj 0 70 30 0 0 0
x3 540 3 9 1 0 0
x4 450 5 5 0 1 0
x5 720 9 3 0 0 1
①第一行是目标函数的系数,第2~4行是约束条件的系数
②第一列是约束方程的常数项
③对于目标函数的更新我们同样采用矩阵的变换,所以obj对应的第一列表示的是目标函数的相反数
"""
"""
运行如下代码后得到的结果如下所示
最终的最优单纯性法是:
b x1 x2 x3 x4 x5
obj -5700 0 0.0 0 -2.0 -6.666667
x3 180 0 0.0 1 -2.4 1.000000
x2 15 0 1.0 0 0.3 -0.166667
x1 75 1 0.0 0 -0.1 0.166667
目标函数的值: 5700
最优决策变量是:
x1 = 75
x2 = 15
"""
matrix = pd.DataFrame(
data=np.array([
[0,70,30,0,0,0],
[540,3,9,1,0,0],
[450,5,5,0,1,0],
[720,9,3,0,0,1]
]),
index=['obj','x3','x4','x5'],
columns=['b','x1','x2','x3','x4','x5']
)
# 判断检验数是否大于0
c = matrix.iloc[0, 1:]
while c.max() > 0:
c = matrix.iloc[0, 1:]
# 选择入基的变量
in_x = c.idxmax() # 该函数运行的结果是x1,即入基变量
in_x_v = c[in_x] # 得到入基变量的系数
# 选择出基变量,即要计算θ的值,并比较大小
b = matrix.iloc[1:,0]
# 选择入基变量对应的列
in_x_a = matrix.iloc[1:][in_x]
# 得到出基变量
out_x = (b/in_x_a).idxmin()
# 完成入基和出基的操作,即对矩阵做初等行变化
matrix.loc[out_x,:] = matrix.loc[out_x,:] / matrix.loc[out_x][in_x]
for idx in matrix.index:
if idx != out_x:
matrix.loc[idx, :] = matrix.loc[idx, :] - matrix.loc[out_x, :]*matrix.loc[idx,in_x]
# 索引变换
index = matrix.index.tolist() # 得到所以行索引的值
i = index.index(out_x) # 得到出基变量的下标
index[i] = in_x
matrix.index = index
# 输出结果
print("最终的最优单纯性法是:")
print(matrix)
print("目标函数的值:",- matrix.iloc[0,0])
# 列的数量减去行的数量得到非基变量的数量,且非基变量一定是下标在前的变量
# 比如非基变量的个数为2,则非基变量一定是x1,x2
print("最优决策变量是:")
x_count = (matrix.shape[1] - 1) - (matrix.shape[0] - 1)
X = matrix.iloc[0, 1:].index.tolist()[:x_count]
for xi in X:
print(xi,"=",matrix.loc[xi,'b'])以上即是对单纯形法的简单概述,内容参考书目《python最优化算法实战》,笔者认为这一部分书中的计算存在问题,如有错误还请批评指正。