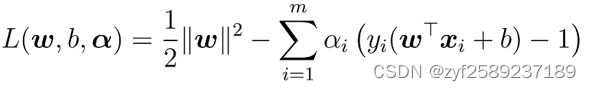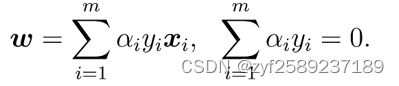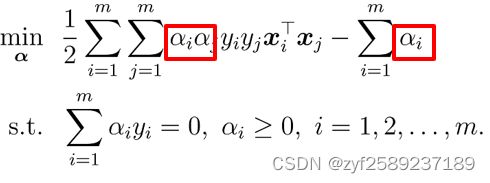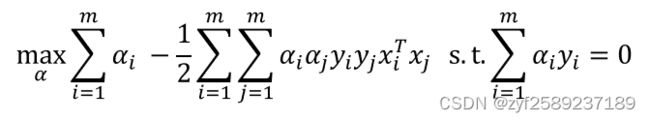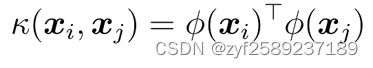机器学习:支持向量机
SVM简介
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法
SVM算法原理
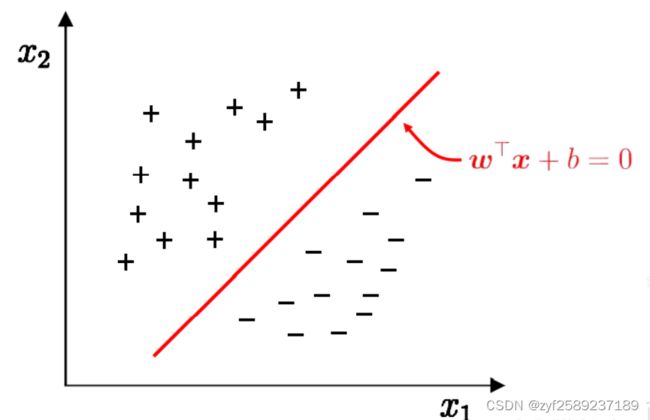
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示, w⋅x+b=0 即为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。
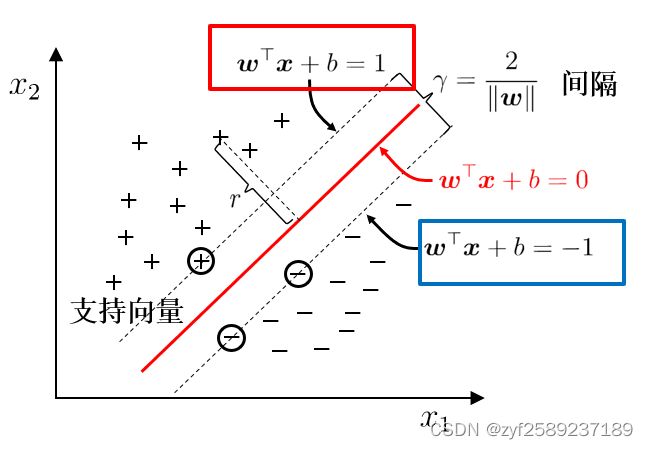
最大间隔与分类
如果一个线性函数能够将样本分开,称这些数据样本是线性可分的。线性函数在二维空间中就是一条直线,在三维空间中就是一个平面,以此类推,如果不考虑空间维数,这样的线性函数统称为超平面。我们看一个简单的二维空间的例子,+代表正类,-代表负类,样本是线性可分的,但是很显然不只有这一条直线可以将样本分开,而是有无数条,我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。在样本空间中寻找一个超平面, 将不同类别的样本分开。
最大化间隔: 寻找参数w和b , 使得下述公式最大:
对偶问题
最大间隔问题的拉格朗日乘法
第一步:引入拉格朗日乘子 αi≥0得到拉格朗日函数
第二步:令L(w,b,α) 对w和b的偏导为零
第三步:w, b回代到第一步
求解SMO
基本思路:不断执行如下两个步骤直至收敛.
第一步:选取一对需更新的变量αi和 αj.
第二步:固定αi和 αj以外的参数, 求解对偶问题更新αi和 αj.
仅考虑αi和 αj时, 对偶问题的约束变为
偏移项b:通过支持向量来确定.
算法流程:每次选取两个α进行更新
核函数
基本想法:不显式地构造核映射, 而是设计核函数.
Mercer定理(充分非必要):只要对称函数值所对应的核矩阵半正定, 则该函数可作为核函数.
常用核函数:
Python实现
准备一个简单的数据集
源码
import matplotlib.pyplot as plt
import numpy as np
import random
def loadDataSet(fileName):
dataMat = [];
labelMat = []
fr = open(fileName)
for line in fr.readlines(): # 逐行读取,滤除空格等
lineArr = line.strip().split()
dataMat.append([float(lineArr[0]), float(lineArr[1])]) # 添加数据
labelMat.append(float(lineArr[2])) # 添加标签
return dataMat, labelMat
def showDataSet(dataMat, labelMat):
data_plus = [] # 正样本
data_minus = [] # 负样本
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) # 转换为numpy矩阵
data_minus_np = np.array(data_minus) # 转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) # 正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) # 负样本散点图
plt.show()
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
# 转换为numpy的mat存储
dataMatrix = np.mat(dataMatIn);
labelMat = np.mat(classLabels).transpose()
# 初始化b参数,统计dataMatrix的维度
b = 0;
m, n = np.shape(dataMatrix)
# 初始化alpha参数,设为0
alphas = np.mat(np.zeros((m, 1)))
# 初始化迭代次数
iter_num = 0
# 最多迭代matIter次
while (iter_num < maxIter):
alphaPairsChanged = 0
for i in range(m):
# 步骤1:计算误差Ei
fXi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
Ei = fXi - float(labelMat[i])
# 优化alpha,设定一定的容错率。
if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
# 随机选择另一个与alpha_i成对优化的alpha_j
j = selectJrand(i, m)
# 步骤1:计算误差Ej
fXj = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
Ej = fXj - float(labelMat[j])
# 保存更新前的aplpha值,使用深拷贝
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
# 步骤2:计算上下界L和H
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H: print("L==H"); continue
# 步骤3:计算eta
eta = 2.0 * dataMatrix[i, :] \
* dataMatrix[j,:].T - dataMatrix[i,:]\
* dataMatrix[i,:].T - dataMatrix[j,:]\
* dataMatrix[j, :].T
if eta >= 0: print("eta>=0"); continue
# 步骤4:更新alpha_j
alphas[j] -= labelMat[j] * (Ei - Ej) / eta
# 步骤5:修剪alpha_j
alphas[j] = clipAlpha(alphas[j], H, L)
if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小"); continue
# 步骤6:更新alpha_i
alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
# 步骤7:更新b_1和b_2
b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[
j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[
j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
# 步骤8:根据b_1和b_2更新b
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2) / 2.0
# 统计优化次数
alphaPairsChanged += 1
# 打印统计信息
print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num, i, alphaPairsChanged))
# 更新迭代次数
if (alphaPairsChanged == 0):
iter_num += 1
else:
iter_num = 0
print("迭代次数: %d" % iter_num)
return b, alphas
def selectJrand(i, m):
j = i # 选择一个不等于i的j
while (j == i):
j = int(random.uniform(0, m))
return j
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def showClassifer(dataMat, w, b):
# 绘制样本点
data_plus = [] # 正样本
data_minus = [] # 负样本
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) # 转换为numpy矩阵
data_minus_np = np.array(data_minus) # 转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7) # 正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) # 负样本散点图
# 绘制直线
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2
plt.plot([x1, x2], [y1, y2])
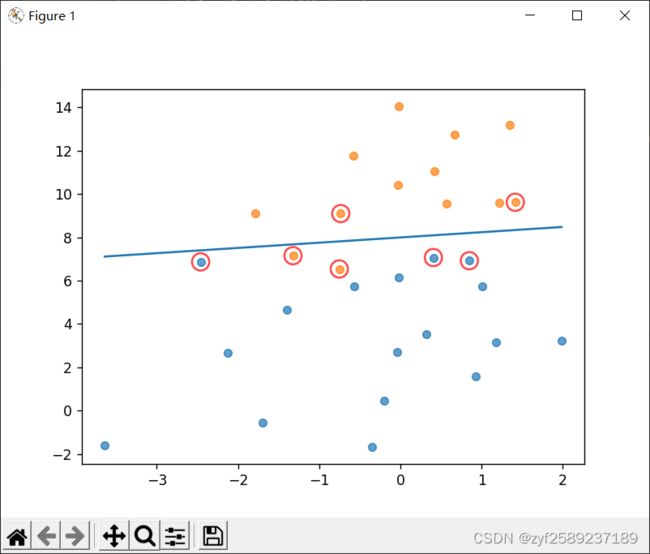
# 找出支持向量点
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.show()
def get_w(dataMat, labelMat, alphas):
alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
return w.tolist()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet('testSet1.txt')
b, alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
w = get_w(dataMat, labelMat, alphas)
showClassifer(dataMat, w, b)
运行结果
小结
SVM的一般流程:
1.收集数据:可以使用任何方法
2.准备数据:需要数值型数据
3.分析数据:有助于可视化分隔超平面
4.训练算法:SVM的大部分时间都源自训练,该过程主要实现两个参数的调优
5.测试算法:十分简单的过程就可以实现
6.使用算法:几乎所有分类问题都可以使用SVM,值得一提的是,SVM本身是一个二分类器,对多类问题应用SVM需要对代码做一些修改
优点:泛化错误率低,计算开销不大,结果易解释。
缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适用于处理二类问题。
适用数据类型:数值型和标称型数据。
支持向量机的泛化错误率较低,也就说它具有良好的学习能力,且学到的结果具有较好的推广性。这些优点是的支持向量机十分流行,被认为是监督学习中最好的定式算法之一。