机器学习二：支持向量机

Reference:

1. Support Vector Machines
2. 周志华《机器学习》

相关文章：拉格朗日乘子法

1. 介绍

SVM 是支持向量机(Support Vector Machine)的简称。简单来说，支持向量机所做的就是去寻找两类数据之间的分隔线，或者通常称为超平面(hyperplane)。

假设我们有训练样本集 $D=\left\{\left({\mathbf{x}}_1,y_1\right),\left({\mathbf{x}}_2,y_2\right),\dots ,\left({\mathbf{x}}_m,y_m\right)\right\},y_i\in \{-1,+1\}$，其中有两类数据。支持向量机是一种算法，把这些点作为输入数据。如果可能的话，输出一条线，来将这些数据分类。

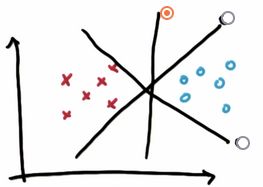
显然，图片中的三条线都能够把不同类别的数据点分隔开，一侧是叉，另一侧是圆圈。但选中的这条线是最好的分割线，为什么呢？

该划分超平面对训练样本局部扰动的"容忍”性最好，它最大化了到最近点的距离，并且对于左右两个类别都是如此。例如，由于训练集的局限性或噪声的因素，训练集外的样本可能比上图中的训练样本更接近两个类的分隔界，这将使许多划分超平面出现错误，而选中的超平面受影响最小。换言之，这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。

在样本空间中，划分超平面可通过如下线性方程来描述：
$${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$$

其中 $\mathbf{w}=\left(w_1;w_2;\dots ;w_d\right)$ 为法向量，决定了超平面的方向；$b$ 为位移项，决定了超平面与原点之间的距离。显然，划分超平面可以被法向量 $\mathbf{w}$ 和位移 $b$ 确定，记为 $(\mathbf{w},b)$。样本空间中任意点 $\mathbf{x}$ 到超平面 $(\mathbf{w},b)$ 的距离可写为：
$$r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert }$$

假设超平面 $(\mathbf{w},b)$ 能将训练样本正确分类，即对于 $({\mathbf{x}}_{\mathbf{i}},y_i)\in D$，

• 若 $y_i=+1$，则有 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_{\mathbf{i}}+b>0$；
• 若 $y_i=-1$，则有 ${\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_{\mathbf{i}}+b<0$。

则：
$$\{\begin{array}{ll}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾+1,& y_i=+1\\ {\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩽-1,& y_i=-1\end{array}$$

如下图所示，距离超平面最近的几个圈起来的训练样本点使上面公式的等号成立，它们被称为"支持向量" (support vector)，两个异类支持向量到超平面的距离之和为：
$$\gamma =\frac{2}{\Vert \mathbf{w}\Vert }$$

而这个距离通常被称之为间隔(margin)，就是线与两个分类中最近点之间的距离。支持向量机首先保证分类正确，在此前提下，再最大化间隔。

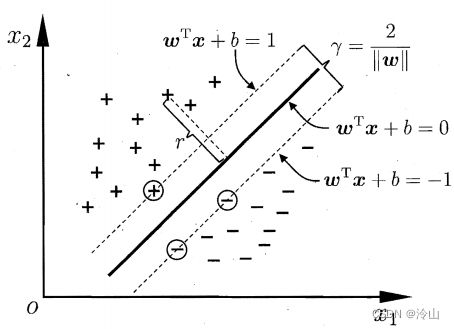
欲找到具有最大间隔(maximum margin)的划分超平面，也就是要找到能满足约束的参数 $\mathbf{w}$ 和 $b$，使得 $\gamma$ 最大，即：
$$\begin{array}{rl}\underset{\mathbf{w},b}{\max }& \frac{2}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m.\end{array}$$

显然，为了最大化问隔，仅需最大化 $\Vert \mathbf{w}{\Vert }^{-1}$，这等价于最小化 $\Vert \mathbf{w}{\Vert }^2$ . 于是，上式可重写为：
Eq.1：
$$\begin{array}{rl}\underset{\mathbf{w},b}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m.\end{array}$$

这就是支持向量机 (Support Vector Machine，SVM)的基本型。

2. 对偶问题

现在问题来到了如何获得最大化的间隔。我们希望求解式 Eq.1 来得到大间隔划分超平面所对应的模型：
$$f(\mathbf{x})={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

其中 $\mathbf{w}$ 和 $b$ 是模型参数。Eq.1 本身是一个凸二次规划(convex quadratic programming)问题，能直接用现成的优化计算包求解，但可以用更高效的办法。

可以看到，Eq.1 是有约束项的，对其使用拉格朗日乘子法可得到其对偶问题。具体来说，对 Eq.1 的每条约束添加拉格朗日乘子 ${\alpha }_i⩾0$，则该问题的拉格朗日函数可写为：
Eq.2：
$$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\right)$$

其中 $\mathbf{\alpha }=\left({\alpha }_1;{\alpha }_2;\dots ;{\alpha }_m\right)$。令 $L(\mathbf{w},b,\mathbf{\alpha })$ 对 $\mathbf{w}$ 和 $b$ 的偏导为零可得
$$\begin{array}{rl}\mathbf{w}& =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i\\ 0& =\sum _{i=1}^m{\alpha }_i{y}_i\end{array}$$

扩展 Eq.2，我们有：$$\frac{1}{2}\stackrel{{\alpha }^{\top }A\alpha }{{\mathbf{w}}^{\top }\mathbf{w}}-\stackrel{{\alpha }^{\top }A\alpha }{\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^{\top }{\mathbf{x}}_i}-\stackrel{0}{b\sum _{i=1}^m{\alpha }_i{y}_i}+\sum _{i=1}^m{\alpha }_i$$

将式子带入 Eq.2，即可将 $L(\mathbf{w},b,\mathbf{\alpha })$ 中的 $\mathbf{w}$ 和 $b$ 消去，并考虑 $0={\sum }_{i=1}^m{\alpha }_i{y}_i$ 的约束，可以得到 Eq.1 的对偶问题：
Eq.3：
$$\begin{gathered} \underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j \\ \text{ s.t. }\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ {\alpha }_i⩾0,i=1,2,\dots ,m. \end{gathered}$$

解出 $\mathbf{\alpha }$ 后，求出 $\mathbf{w}$ 和 $b$ 即可得到模型：
Eq.4：
$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i^{\mathrm{T}}\mathbf{x}+b.\end{array}$$

从对偶问题 Eq.3 解出的问是式 Eq.2 中的拉格朗日乘子，它正好对应着训练样本 $({\mathbf{x}}_i,y_i)$。注意到式 Eq.1 中有不等式约束，因此上述过程需满足 KKT(Karush-Kuhn-Tucker)条件，即要求：
$$\{\begin{array}{l}{\alpha }_i⩾0\\ y_{i}f\left({\mathbf{x}}_i\right)-1⩾0\\ {\alpha }_i\left(y_{i}f\left({\mathbf{x}}_i\right)-1\right)=0.\end{array}$$

于是, 对任意训练样本 $\left({\mathbf{x}}_i,y_i\right)$，总有 ${\alpha }_i=0$ 或 $y_{i}f\left({\mathbf{x}}_i\right)=1$。若 ${\alpha }_i=0$, 则该样本将不会在式 Eq.4 的求和中出现，也就不会对 $f(\mathbf{x})$ 有任何影响；若 ${\alpha }_i>0$，则必有 $y_{i}f\left({\mathbf{x}}_i\right)=1$，所对应的样本点位于最大间隔边界上，是一个支持向量。这显示出支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需保留，最终模型仅与支持向量有关。

3. 非线性数据

现在给出一个比较复杂的数据集，它有很多聚集在 $x$ 和 $y$ 坐标系原点周围的红叉和大部分位于红叉外围的蓝色圆圈组成。根据前面所说支持向量机内容，无法对这组数据给出一个理想的分类结果------这两个类之间不存在明显的线性超平面(不存在线性分隔器来区分这两个类，即很难在两个类之间画一条线)。但实际上，支持向量机可以对这样的数据进行分类。

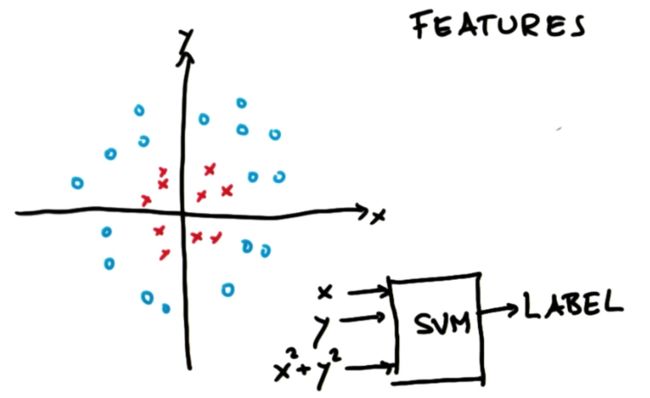
我们认为我们把数据特征 $x$ 和 $y$ 输入到一个神奇的大盒子，也就是支持向量机里，输出是一个标签，标签是蓝圈或红叉。现在挑选一个对这组数据有帮助的特征，就是 $x^2+y^2$。这时现在有一个三维的输入空间。

我们将这个新的 $x^2+y^2$ 特征称为 $z$。这里 $x,y$ 的超平面与原点之间的距离 $z$ 始终为非负数。神奇的是，所有红叉离原点的距离都很小；所有蓝圆圈离原点的距离都很大。
这时图中 $x-z$ 坐标系内的数据是可以线性分割的。更有趣的是，图中线性可分的线对应着原始数据中的圆，它由坐标系中与原点距离相等的一系列点组成。因此，选择一个较为合适的新特征，就能让支持向量机学习圆形的非线性决策面，这是非常神奇的。简单来说，这里用到的方法，就是将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

3.1 核函数与核技巧

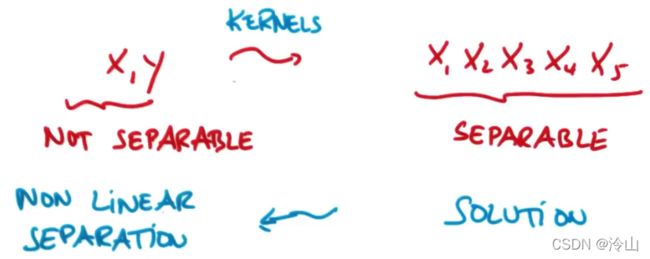
上面这种方法看起来确实很有用，但也确实很难，需要写一些新的特征，而支持向量机最棒的一点在于并不需要这么做。

有一种函数，它们接收低纬度的输入空间或特征空间，并将其映射到高维度空间。所以，过去不可线性分隔的内容变为可分隔--------这些函数被称为核函数。该方法被称为核技巧(kernel trick)。

这些不仅是具有特征空间的函数，而且是超过两个输入的函数。应用核函数技巧将输入空间从 $x,y$ 变换到更大的输入空间后，再使用支持向量机对数据点进行分类，得到解以后返回原始空间，这样就能得到一个非线性分隔，这是支持向量机的一个重要优点。

可以便捷地找到最佳的线性分类器或不同类之间的线性分隔线，在更高维度空间应用所谓的核技巧就能够实现一个极其强大的功能-----它是机器学习最主要的技巧之一。

3.1.1 数学解释

1. 基函数：显式特征映射(implicit feature map)；
2. 核函数：隐式特征映射(explicit feature map)。

特征映射指的是函数 $\varphi :{\mathbb{R}}^n\to {\mathbb{R}}^N$
$$\varphi (\mathbf{x})={\left({\varphi }_1(\mathbf{x}),\dots ,{\varphi }_N(\mathbf{x})\right)}^{\top },\mathbf{x}\in {\mathbb{R}}^n$$

• ${\varphi }_1(\mathbf{x}),\dots ,{\varphi }_N(\mathbf{x})$ 被称为 基函数(basis functions)；
• 向量 $\varphi (\mathbf{x})$ 被称为特征向量而空间 $\varphi (\mathbf{x}):\mathbf{x}\in {\mathbb{R}}^n$ 被称为特征空间。

令 $\varphi (\mathbf{x})$ 表示将 $\mathbf{x}$ 映射后的特征向量，于是在特征空间中划分超平面所对应的模型可表示为：
$$f(\mathbf{x})={\mathbf{w}}^{\mathrm{T}}\varphi (\mathbf{x})+b$$

其中 $\mathbf{w}$ 和 $b$ 是模型参数。
类似式 Eq.1，有
$$\begin{array}{rl}\underset{\mathbf{w},b}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}\varphi \left({\mathbf{x}}_i\right)+b\right)⩾1,i=1,2,\dots ,m\end{array}$$

其对偶问题是:
Eq.5：
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right) \\ \begin{array}{ll}\text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i⩾0,i=1,2,\dots ,m.\end{array} \end{gathered}$$

求解式 Eq.5 涉及到计算 $\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$，这是样本 ${\mathbf{x}}_i$ 与 ${\mathbf{x}}_j$ 映射到特征空间之后的内积。由于特征空间维数可能很高，甚至可能是无穷维，因此直接计算 $\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$ 通常是困难的。为了避开这个障碍，可以设想这样一个函数:
$$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩=\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$$

即 ${\mathbf{x}}_i$ 与 ${\mathbf{x}}_j$ 在特征空间的内积等于它们在原始样本空间中通过函数 $\kappa (\cdot ,\cdot )$ 计算的结果。有了这样的函数, 我们就不必直接去计算高维甚至无穷维特征空间中的内积，于是式 Eq.5 可重写为：
$$\begin{array}{rl}\underset{\alpha }{\max }& \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\\ \text{ s.t. }& \sum _{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i⩾0,i=1,2,\dots ,m.\end{array}$$

求解后即可得到：
$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa \left(\mathbf{x},{\mathbf{x}}_i\right)+b\end{array}$$

这里的函数 $\kappa (\cdot ,\cdot )$ 就是 核函数(kernel function)。上式显示出模型最优解可通过训练样本的核函数展开，这一展式也被称为支持向量展式(support vector expansion)。显然，若已知合适映射 $\varphi (\cdot )$ 的具体形式, 则可写出核函数 $\kappa (\cdot ,\cdot )$，但在现实任务中我们通常不知道 $\varphi (\cdot )$ 是什么形式。我们希望样本在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能至关重要。需注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也仅是隐式地定义了这个特征空间。于是，"核函数选择"成为支持向量机的最大变数。若核函数选择不合适，则意味着将样本映射到了一个不合适的特征空间，很可能导致性能不佳。

3.1.2 几种常用的核函数

$$\begin{array}{lll}\text{ 名称 }& \text{ 表达式 }& \text{ 参数 }\\ \text{ 线性核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j& \\ \text{ 多项式核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\right)}^d& d⩾1\text{ 为多项式的次数 }\\ \text{ 高斯核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{2{\sigma }^2}\right)& \sigma >0\text{ 为高斯核的带宽(width) }\\ \text{ 拉普拉斯核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }{\sigma }\right)& \sigma >0\\ \text{ Sigmoid 核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\tanh \left(\beta {\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j+\theta \right)& \tanh \text{ 为双曲正切函数, }\beta >0,\theta <0\end{array}$$

此外, 还可通过函数组合得到, 例如:

• 若 ${\kappa }_1$ 和 ${\kappa }_2$ 为核函数, 则对于任意正数 ${\gamma }_1$、${\gamma }_2$，其线性组合也是核函数：
  $${\gamma }_1{\kappa }_1+{\gamma }_2{\kappa }_2$$

• 若 ${\kappa }_1$ 和 ${\kappa }_2$ 为核函数，则核函数的直积也是核函数：
  $${\kappa }_1\otimes {\kappa }_2(\mathbf{x},\mathbf{z})={\kappa }_1(\mathbf{x},\mathbf{z}){\kappa }_2(\mathbf{x},\mathbf{z})$$

• 若 ${\kappa }_1$ 为核函数，则对于任意函数 $g(\mathbf{x})$ 也是核函数：
  $$\kappa (\mathbf{x},\mathbf{z})=g(\mathbf{x}){\kappa }_1(\mathbf{x},\mathbf{z})g(\mathbf{z})$$

4. SVM 响应离群点

有时候，似乎支持向量机无法对某些问题进行正确分类。例如，可能有这样的一个数据集，很显然，将两个类分割的决策面是不存在的，可以将下面的这个点当作 outlier。所以问题是，这时候希望支持向量机怎么做？

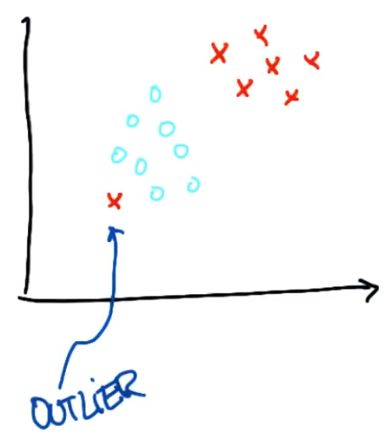
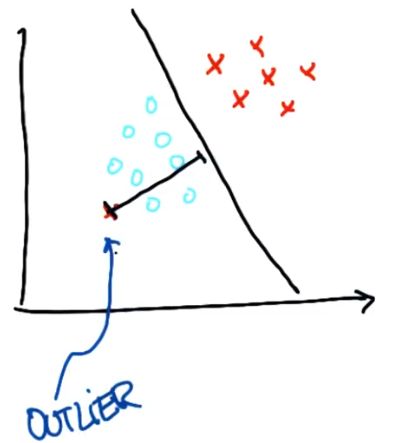
最好的情况，就是作出一个决策边界，直接把错误分类的那一点放在另一边-----支持向量机完全可以做到这一点，他们经常能找到一条决策边界，使两个数据集的间隔最大化同时容忍个别异常值，就像这里所展示的。

4.1 软间隔

在前面的讨论中，一直假定训练样本在样本空间或特征空间中是线性可分的，即存在一个超平面能将不同类的样本完全划分开。然而，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步说，即使恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。

缓解该问题的一个办法是允许支持向量机在一些样本上出错。为此，要引入软间隔(soft margin)的概念。如图所示，红色圈出了一些不满足约束的样本：

前面介绍的支持向量机形式是要求所有样本均满足约束，使所有样本都必须划分正确，这称为硬间隔(hard margin)，而软间 隔则是允许某些样本不满足约束条件：$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1$。

在最大化间隔的同时，不满足约束的样本应尽可能少。于是，优化目标可写为：
Eq.6：
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\ell }_{0/1}\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)$$

其中 $C>0$ 是一个常数, ${\ell }_{0/1}$ 是 “ $0/1$ 损失函数”
$${\ell }_{0/1}(z)=\{\begin{array}{ll}1,& \text{ if }z<0\\ 0,& \text{ otherwise }\end{array}$$

当 $C$ 取无限大时，式 Eq.6 迫使所有样本均满足约束；而当 $C$ 取有限值时，Eq.6 允许一些样本不满足约束。

然而，${\ell }_{0/1}$ 非凸、非连续，数学性质不太好，使得式 Eq.6 不易直接求解。于是，人们通常用其他一些函数来代替 ${\ell }_{0/1}$，称为替代损失(surrogate loss)。替代损失函数一般具有较好的数学性质，如它们通常是凸的连续函数且是 ${\ell }_{0/1}$ 的上界。下图给出了三种常用的替代损失函数：

即：

• hinge 损失：${\ell }_{\text{hinge }}(z)=\max (0,1-z)$；
• 指数损失(exponential loss)：${\ell }_{\exp }(z)=\exp (-z)$；
• 对率损失(logistic loss)：${\ell }_{\log }(z)=\log (1+\exp (-z))$。

若采用 hinge 损失，则式 Eq.6 变成：
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^{m}max\left(0,1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\right)$$

引入松弛变量(slack variables) ${\xi }_i⩾0$，可将上面公式重写为：
$$\begin{array}{rl}\underset{\mathbf{w},b,{\xi }_i}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\xi }_i\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ & {\xi }_i⩾0,i=1,2,\dots ,m.\end{array}$$

这就是常用的 软间隔支持向量机。

4.2 正则化

4.3 参数调整

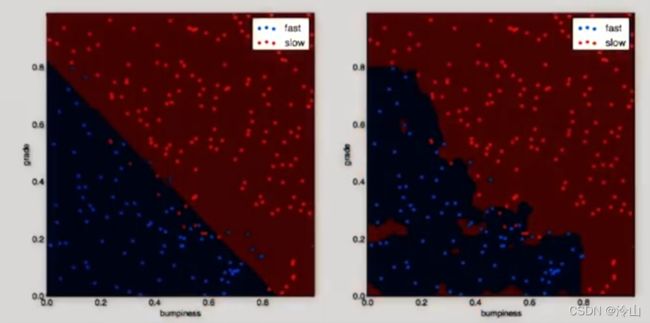
创建分类器时要传递到形参的自变量称为实参。在 SVM 中，参数就是 核 和即将要讨论的另外连个参数：$C$(软间隔) 和 $\gamma$(正则化)。下图中的两个 SVM 有不同的核函数，其中左侧的那个是线性函数(linear)，右侧的那个是径向基函数(rbf)：

4.3.1 SVM C Parameter

SVM 的一个重要参数是 $C$ 参数，它会在光滑的决策边界以及尽可能正确分类所有训练点两者之间进行平衡。假设我们的数据如下图：
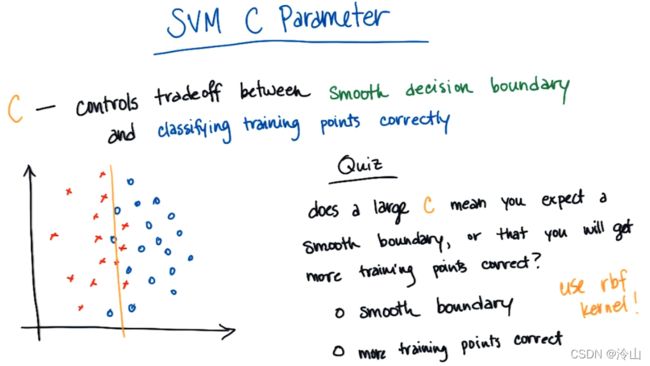可以画出可能是非常直的线，其代价是有少数的点分类错误；也可以画出相当曲折的线，基本上所有的训练点都被分类正确。然而，选择一个复杂模型是有代价的-------像这样复杂的模型，可能有一定的概率对于测试集的泛化能力不够。有些会稍微直一些、稍微更直接些，在开始观察测试集的准确度时可能实际上是更好的选择。

$C$ 值越大，就意味着对更多训练点进行正确分类。实际上其含义就是 $C$ 值越大，就可以得到更复杂的决策边界。它可以弯曲绕过单独的数据点尽可能让所有训练的分类都正确。但代价是，可能比想要的结果复杂一些。希望决策边界的形状接近于直线的程度有多少、希望如何平衡光滑决策边界和训练点正确分类这两者，这些是机器学习的很关键的灵活部分。

4.3.2 SVM Gamma Parameter

$\gamma$ 定义单个训练样本对结果作用范围的远近，较小的 $\gamma$ 值意味着每个点都可能对最终结果产生作用；反之，较大的 $\gamma$ 值意味着训练样本只对距离较近的决策边界有影响。

如下图中，如果 $\gamma$ 值较大，决策边界的具体细节将取决于距离边界非常近的点。这些影响结果的数据点非常接近边界，在一定程度上忽略了距离决策边界较远的点。如果 $\gamma$ 值较小，那么即使距离决策边界较远的点，也会对决策边界具体形状产生影响。这样造成的影响在于，尤其对于 $\gamma$ 较大的情况下 会给出一条相当曲折的决策边界。

也就是说，$\gamma$ 值较大时，近距离的点极大改变了决策边界的方向，从而最终使该点位于边界正确的一侧；如果 $\gamma$ 值较小，靠近决策边界的这些点的重要程度会相对降低。这时下图例子中，最终得到的决策边界线性度和平滑度更高、曲折的程度则更低。

注意，线性核只能使用参数 $C$ 来调优；而对于非线性核，可以调整 $C$ 和 $\gamma$！

5. Overfitting

下图这个例子中，决策边界非常复杂，像这样的情形，被称为过拟合。这是机器学习中常见的。

举个例子，在下面这一组数据，看起来可以被图中绿色的直线分隔。而图中有一个在红色与蓝色之间的黑色决策面，红蓝数据被正确分类，但决策面的其他很多位置看上去非常奇怪。如果仅仅是照搬原始数据对其进行分类，机器学习算法就会产生类似的复杂结果，而不是产生像直线这样的简单结果，这就意味着出现了过拟合。
在机器学习中，要避免过拟合。控制过拟合的方法之一就是，通过调整算法中的参数 $c$，$\gamma$ 以及 核函数。

6. 总结

对于具有明显的分隔边界的复杂数据支持向量机的表现十分出色；对于海量数据，它们的表现不太好-----------因为在这种规模的数据集中，训练时间与数据量的三次方成正比。对于数据集噪声过大情况，支持向量机的效果也不好。

所以，如果类之间的重叠较多，且需要将不同类分隔开，此时朴素贝叶斯分类器会更有效。

所以，拥有的数据集和可用特征上，如果有一个海量数据集且有很多特征，现成的支持向量机程序运行速度可能会很慢，数据中的某些噪声也可能会导致过拟合现象。所以，需要在测试数据集上进行测试看看它的表现如何，接下来这个训练后的模型就可以用了。

7. SK Learn

支持向量机(SVMs) 是一套用于分类、回归和异常值检测的监督学习方法。

支持向量机的优点有：

• 在高维空间有效；
• 在维数大于样本数的情况下仍然有效；
• 在决策函数(被称为支持向量)中使用训练点的子集，因此它也是内存高效的；
• 多功能:可以为决策函数指定不同的核函数。提供了通用核，但也可以指定定制核函数。

支持向量机的缺点有：

• 当特征数量远远大于样本数量时，在选择核函数时要避免过拟合，正则化项至关重要；
• 支持向量机不直接提供概率估计，这些是使用代价较大的5倍交叉验证法来计算的。

7.1 分类

SVC、NuSVC 和 LinearSVC 是能够对数据集进行二分类和多分类的类。
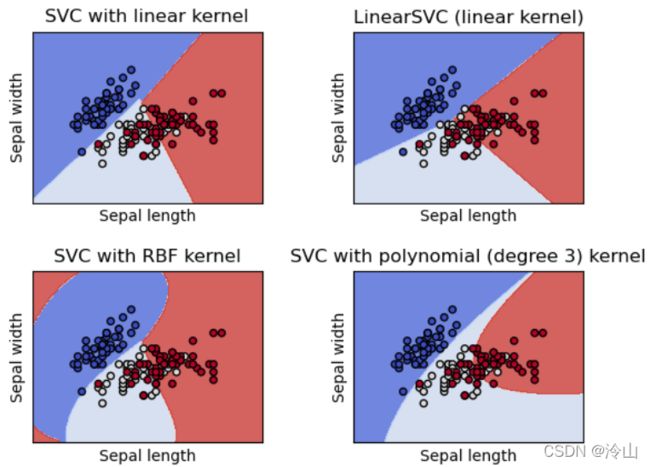
SVC 和 NuSVC 是类似的方法，但接受的参数集略有不同，且有不同的数学公式(见数学公式部分)。而 LinearSVC 是支持向量分类在线性核的情况下的另一个(更快的)实现。请注意，LinearSVC 不接受参数 kernel，因为它被认为是线性的。它也缺少 SVC 和 NuSVC 的一些属性，比如 support_。

与其他分类器一样，SVC、NuSVC 和 LinearSVC 使用两个数组作为输入:一个数组 X(n_samples，n_features) 包含训练样本，一个数组 y (n_samples) 包含类标签(字符串或整数)：

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)
SVC()

在经过拟合后，该模型可以用来预测新的值：

>>> clf.predict([[2., 2.]])
array([1])

支持向量机的决策函数依赖于训练数据的某个子集，称为支持向量。这些支持向量的一些性质可以在属性 support_vectors_、support_ 和 n_support_ 中找到。

>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # get indices of support vectors
>>> clf.support_
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_
array([1, 1]...)

7.1.1 多类别分类

SVC 和 NuSVC 实现了“一对一”的多类分类方法。总共构造了 n_classes * (n_classes - 1) / 2 个分类器，每个分类器从两个类中训练数据。为了提供与其他分类器一致的接口，decision_function_shape 选项允许将“一对一”分类器的结果单调地转换为“一对其余”的形状(n_samples, n_classes) 决策函数。

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(decision_function_shape='ovo')
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

LinearSVC 实现的“一对其余”的多类策略，也训练了 n_classes 模型。

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC()
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

文章跳转：
机器学习一：朴素贝叶斯(Naive Bayes)
机器学习三：决策树
传统物体检测