图解常见树结构
目录
- 1 二叉树
- 2 二叉查找树
-
- 2.1 退化问题
- 3 平衡树
-
- 3.1 二叉平衡搜索树(AVL 树)
- 3.2 “2-3 树”
- 3.3 “2-3-4 树”
- 3.4 B 树
- 4 红黑树
-
- 4.1 红黑树的特点
- 4.2 左旋/右旋
- 4.3 红黑树的插入调整(了解)
- 4.4 红黑树的删除调整(了解)
- 4.5 应用场景
1 二叉树
满足以下两个条件的树就是二叉树:
- 本身是有序树。
- 树中包含的各个节点的度不能超过 2,即只能是 0、1、2。
2 二叉查找树
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树。
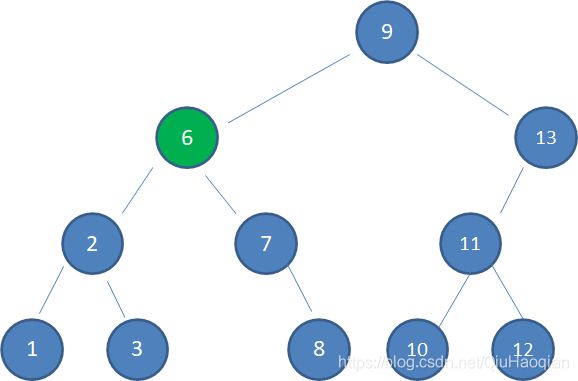
下图为查找值为29的节点的步骤:
- 查看根节点 41。
- 因为 41>29,所以查看 41 的左孩子 20。
- 因为 20<29,所以查看 20 的右孩子29,发现其正好是要查看的节点。
2.1 退化问题
如果数据的插入顺序是从大到小,或是从小到大,会导致二叉查找树退化成单链表的形式。
例如,插入数据依次为 {1,2,3,4,5}(从小到大),则如下图所示:

例如,插入数据依次为 {5,4,3,2,1}(从大到小),则如下图所示:

为了解决该问题,出现了一些解决方法能够使得树趋向平衡,这种自平衡的树叫做平衡树。
3 平衡树
平衡树(Balance Tree,BT)指的是,任意节点的子树的高度差都小于等于 1。
常见的符合平衡树的有 AVL 树(二叉平衡搜索树),B 树(多路平衡搜索树,2-3 树,2-3-4 树中的一种),红黑树等。
3.1 二叉平衡搜索树(AVL 树)
AVL 树是严格平衡的二叉树,任意节点的两个子树的高度差不超过 1。
AVL 树利用自平衡能,对不符合高度差的结构进行调整,解决二叉树退化问题;
例如,插入数据依次为 {1,2,3,4,5}(从小到大),则如下图所示:
3.2 “2-3 树”
2-3 树,是指每个具有子节点的节点要么有两个子节点和一个数据元素,要么有三个子节点和两个数据元素的自平衡的树,它的所有叶子节点都具有相同的高度。
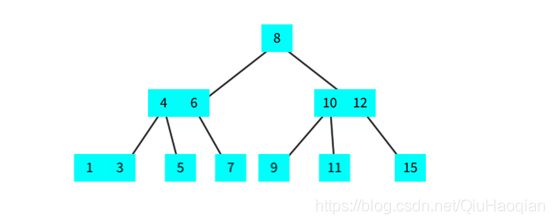
2 节点:包含 2 个子节点 和 1 个数据元素。
3 节点:包含 3 个子节点 和 2 个数据元素。
性质 1:满足二叉搜索树的性质。
性质 2:节点可以存放一个或两个元素。
性质 3:每个节点有两个或三个子节点。
3.3 “2-3-4 树”
2-3-4 树,它的每个非叶子节点,要么是 2 节点,要么是 3 节点,要么是 4 节点,且可以自平衡,所以称作 2-3-4 树。
2 节点:包含 2 个子节点 和 1 个数据元素。
3 节点:包含 3 个子节点 和 2 个数据元素。
4 节点:包含 4 个子节点 和 3 个数据元素。
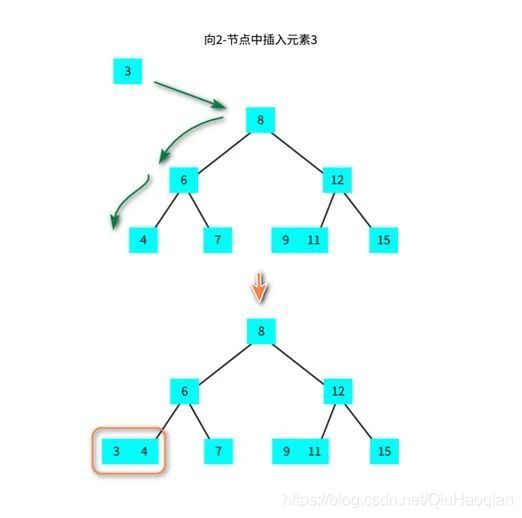
规则 1:加入新元素时,不会往空的位置添加,而是添加到最后一个叶子节点上。
规则 2:4节点被分解为 2节点组成的树
规则 3:分解后新树的根节点需要向上和父节点融合。
插入元素步骤如下:
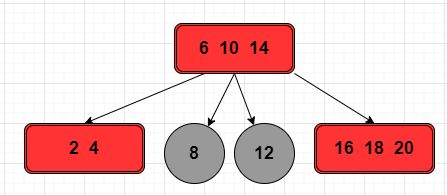
规则 1,插入节点 17 不会加入节点 [16,18,20] 的子树,而是与该节点融合。
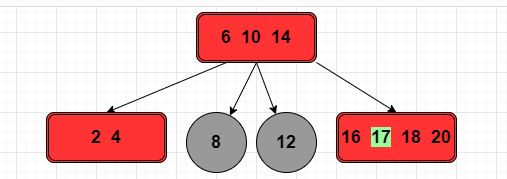
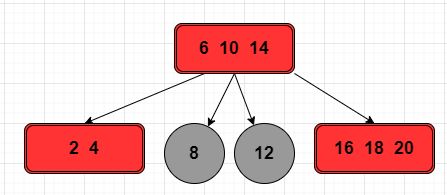
规则 2,节点 [16,17,18,20] 是一个 4 节点,将该节点进行拆解,将 18 作为子树的根节点进行拆分。
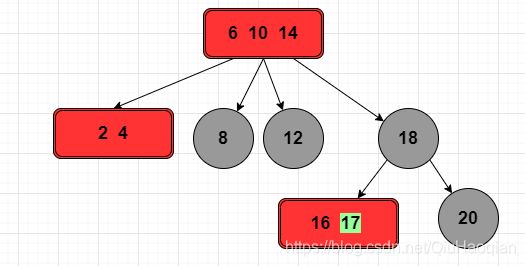
规则三,此时树暂时失去了平衡,需要将拆分后的子树的根节点向上进行融合。
![]()
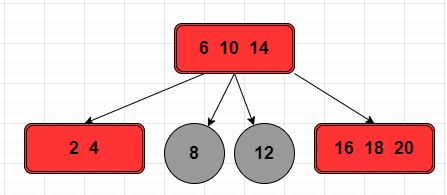
规则 2,节点 [6,10,14,18] 是一个 4 节点,将该节点进行拆解成新的树,将 14 作为子树的根节点进行拆分,完成了 2-3-4 树的构建。
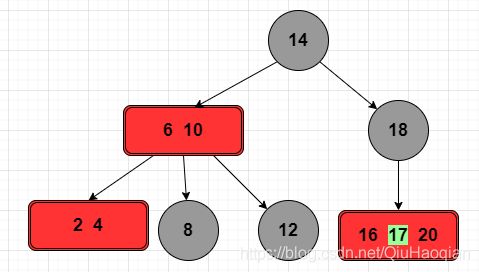
2-3 树,2-3-4 树都有了,那是不是也有 2-3-4-5 树,2-3-4-5–…-n 树的存在呢?
事实上是有的,世人把这一类树称为一个名字:B 树。
3.4 B 树
B 树,表示的是一类树,具有如下特性:
1、 一个节点可以有多于两个子节点;
2、自平衡的;
为了更好地区分一颗 B 树到底属于哪一类树,给它一个新的属性:度(Degree):一个节点能有多少箭头指向其他节点。
具有度为 3 的 B 树,表示一个节点最多有三个子节点,也就是 2-3 树的定义。
具有度为 4 的 B 树,表示一个节点最多有四个子节点,也就是 2-3-4 树的定义。
4 红黑树
R-B Tree,全称是 Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。
4.1 红黑树的特点
1.结点是红色或黑色。
2.根结点是黑色。
3.每个叶子结点都是黑色的空结点(NIL结点)。
4.每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
红黑树的特点能保证 从根节点到叶子结点的最长路径不会超过最短路径的2倍。
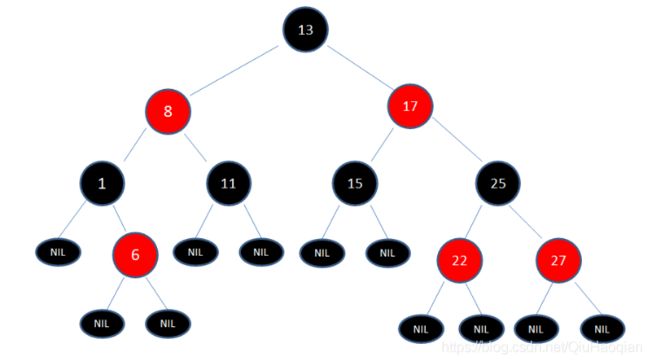
将该红黑树与上文讲到的 2-3-4 树对比,可以发现,红黑树可以看做是一个 2-3-4 树的变形:

当插入或删除节点时,红黑树的5条规则可能被打破。这个时候需要利用 变色与旋转 来调整红黑树使其满足5条规则(调整的情况很多,过程复杂,需要具体情况具体分析,对过程有所了解即可)。
4.2 左旋/右旋
左旋:
逆时针旋转红黑树的两个结点,使得父结点被自己的右孩子取代,而自己成为自己的左孩子。
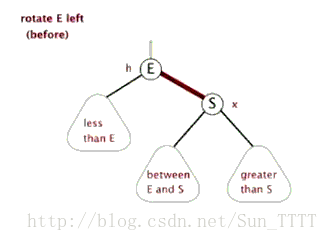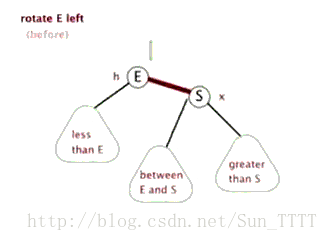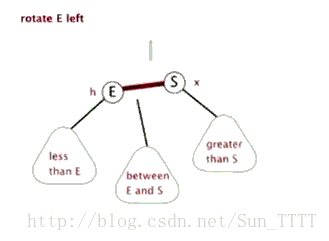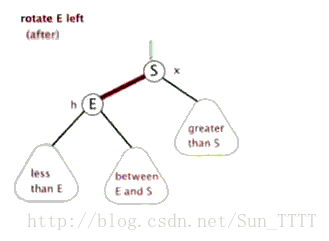
右旋:
顺时针旋转红黑树的两个结点,使得父结点被自己的左孩子取代,而自己成为自己的右孩子。

4.3 红黑树的插入调整(了解)
红黑树插入新节点的时候可以分为5种不同的局面,每种局面有不同的调整方法。
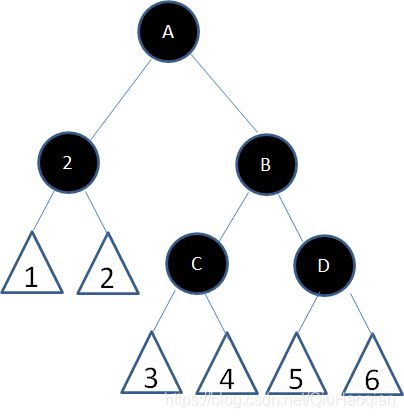
局面1: 新结点(A)位于树根,没有父结点。
空心三角形代表结点下面的子树
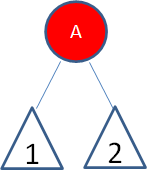
这种局面,直接让新结点变色为黑色,规则2得到满足。同时,黑色的根结点使得每条路径上的黑色结点数目都增加了1,所以并没有打破规则5。
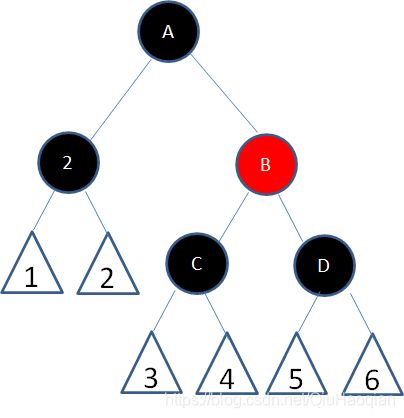
这种局面,新插入的红色结点B并没有打破红黑树的规则,所以不需要做任何调整。
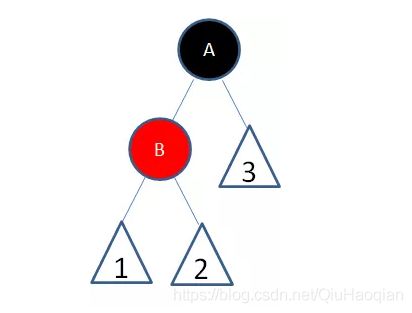
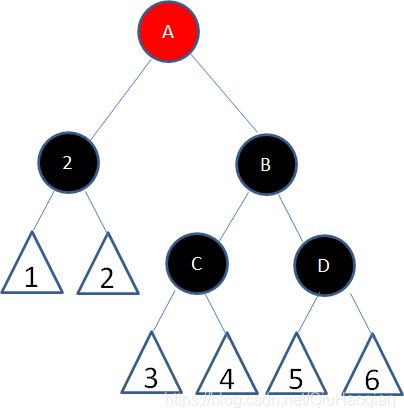
局面3:新结点(D)的父结点和叔叔结点都是红色。

这种局面,两个红色结点B和D连续,违反了规则4。因此我们先让结点B变为黑色:

这样一来,结点B所在路径凭空多了一个黑色结点,打破了规则5。因此我们让结点A变为红色:

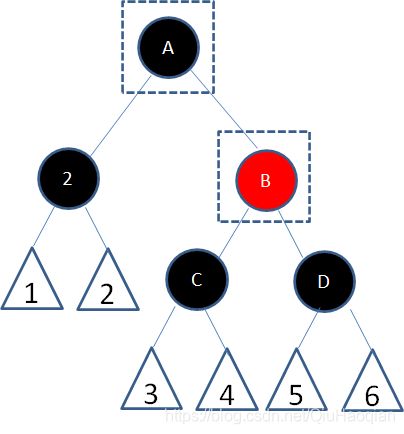
这时候,结点A和C又成为了连续的红色结点,我们再让结点C变为黑色:
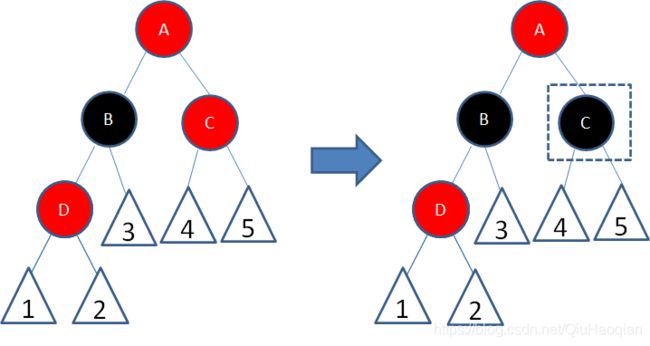
经过上面的调整,这一局部重新符合了红黑树的规则。
局面4:新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的右孩子,父结点(B)是祖父结点的左孩子。
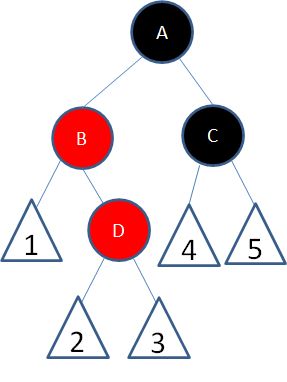
以结点B为轴,做一次左旋转,使得新结点D成为父结点,原来的父结点B成为D的左孩子:

这样一来,进入了局面5。
局面5:新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的左孩子,父结点(B)是祖父结点的左孩子。

以结点A为轴,做一次右旋转,使得结点B成为祖父结点,结点A成为结点B的右孩子:

接下来,我们让结点B变为黑色,结点A变为红色:

经过上面的调整,这一局部重新符合了红黑树的规则。
如果局面4和局面5当中的父结点B是祖父结点A的右孩子该怎么办呢?很简单,如果局面4中的父结点B是右孩子,则成为了局面5的镜像,原本的右旋操作改为左旋;如果局面5中的父结点B是右孩子,则成为了局面4的镜像,原本的左旋操作改为右旋。
下边给出一个实际案例
给定下面这颗红黑树,新插入的结点是21:

显然,新结点21和它的父结点22是连续的红色结点,违背了规则4,应该如何调整呢?
当前的情况符合局面3:“新结点的父结点和叔叔结点都是红色。”
于是首先经过三次变色,22变为黑色,25变为红色,27变为黑色:

经过上面的调整,以结点25为根的子树符合了红黑树规则,但结点25和结点17成为了连续的红色结点,违背规则4。
于是,我们把结点25看做一个新结点,正好符合局面5的镜像:“新结点的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的右孩子,父结点是祖父结点的右孩子”
于是我们以根结点13为轴进行左旋转,使得结点17成为了新的根结点:

接下来,让结点17变为黑色,结点13变为红色:
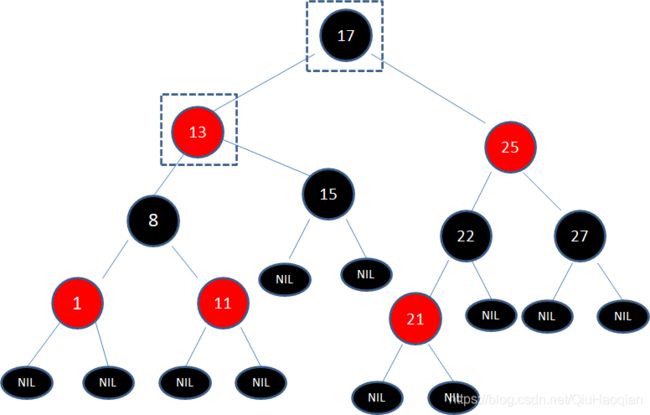
如此一来,我们的红黑树变得重新符合规则。
4.4 红黑树的删除调整(了解)
二叉查找树删除 操作可以分成三种情况。
情况1,待删除的结点没有子结点:

上图中,待删除的结点12是叶子结点,没有子节点,直接删除:

情况2,待删除的结点有一个孩子:
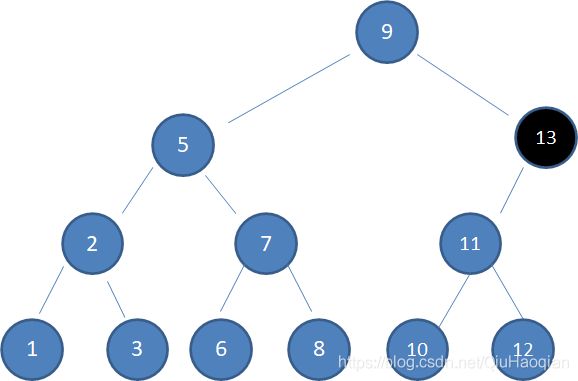
上图中,待删除的结点13只有左孩子,让左孩子结点11取代被删除的结点,结点11以下的结点关系无需变动:

情况3,待删除的结点有两个孩子:

上图中,待删除的结点5有两个孩子,这种情况比较复杂。此时,需要选择与待删除结点最接近的结点来取代它:结点3仅小于结点5,结点6仅大于结点5,两者都是合适的选择。但习惯上选择仅大于待删除结点的结点,也就是结点6来取代节点5。
被选中的结点6,仅大于结点5,因此一定没有左孩子。否则按照情况1或情况2的方式进一步处理。
红黑树的删除 规则需要在二叉树的删除规则上,再经过变色与旋转操作,使其满足二叉树的5条规则。
第一步:如果待删除结点有两个非空的孩子结点,转化成待删除结点只有一个孩子(或没有孩子)的情况。
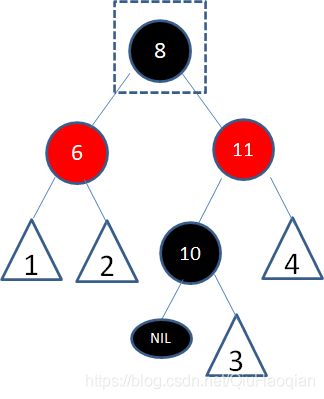
上面例子是一颗红黑树的局部,标数字的三角形代表任意形态的子树,假设结点8是待删除结点。
根据上文讲解的二叉查找树删除流程,由于结点8有两个孩子,我们选择仅大于8的结点10复制到8的位置,结点颜色变成待删除结点的颜色:
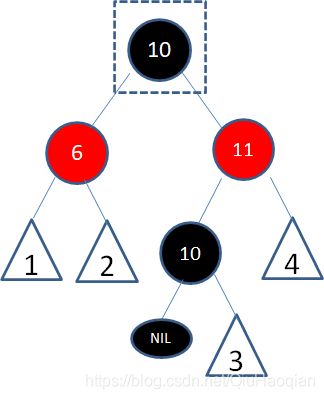
接下来我们需要删除原结点10:
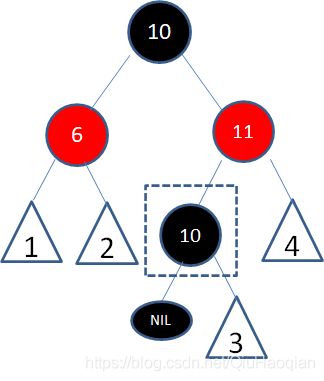
结点10能成为仅大于8的结点,必定没有左孩子结点,所以问题转换成了待删除结点只有一个右孩子(或没有孩子)的情况。接下来我们进入第二步。
第二步:根据待删除结点和其唯一子结点的颜色,分情况处理。
情况1:自身是红色,子结点是黑色:
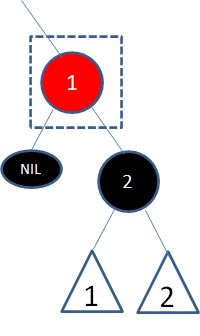
这种情况最简单,按照二叉查找树的删除操作,删除结点1即可:
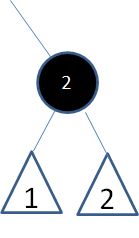
情况2:自身是黑色,子结点是红色:
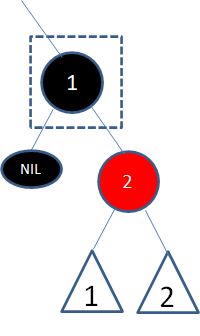
这种情况也很简单,首先按照二叉查找树的删除操作,删除结点1:
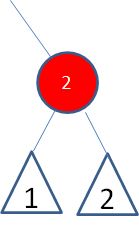
此时,这条路径凭空减少了一个黑色结点,需要把结点2变成黑色即可:

情况3:自身是黑色,子结点也是黑色,或者子结点是空叶子结点:

这种情况最复杂,涉及到很多变化。
首先还是按照二叉查找树的删除操作,删除结点1:
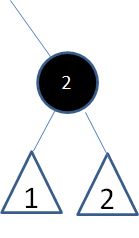
显然,这条路径上减少了一个黑色结点,而且结点2再怎么变色也解决不了。
这时候使用下边讲的第三步,专门解决父子双黑的情况。
第三步:遇到双黑结点,在子结点顶替父结点之后,分成6种子情况处理。
子情况1:结点2是红黑树的根结点:

此时所有路径都减少了一个黑色结点,并未打破规则,不需要调整。
子情况2:结点2的父亲、兄弟、侄子结点都是黑色:
此时,直接把结点2的兄弟结点B改为红色:
这样一来,原本结点2所在的路径少了一个黑色结点,现在结点B所在的路径也少了一个黑色结点,两边“扯平”了。

可是,结点A以下的每一条路径都减少了一个黑色结点,与结点A之外的其他路径又造成了新的不平衡啊?没关系,我们让结点A扮演原先结点2的角色,进行递归操作,重新判断各种情况。
子情况3,结点2的兄弟结点是红色:
首先以结点2的父结点A为轴,进行左旋

然后结点A变成红色、结点B变成黑色:

这样的意义是什么呢?结点2所在的路径仍然少一个黑色结点呀?
别急,这样的变化有可能转换成子情况4、5、6中的任意一种,在子情况4、5、6当中会进一步解决。
子情况4:结点2的父结点是红色,兄弟和侄子结点是黑色:
这种情况,我们直接让结点2的父结点A变成黑色,兄弟结点B变成红色:
这样一来,结点2的路径补充了黑色结点,而结点B的路径并没有减少黑色结点,重新符合了红黑树的规则。
子情况5:结点2的父结点随意,兄弟结点B是黑色右孩子,左侄子结点是红色,右侄子结点是黑色:
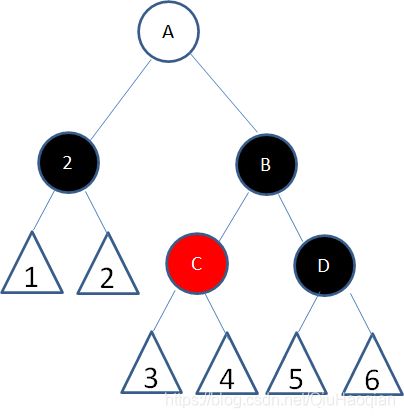
这种情况下,首先以结点2的兄弟结点B为轴进行右旋
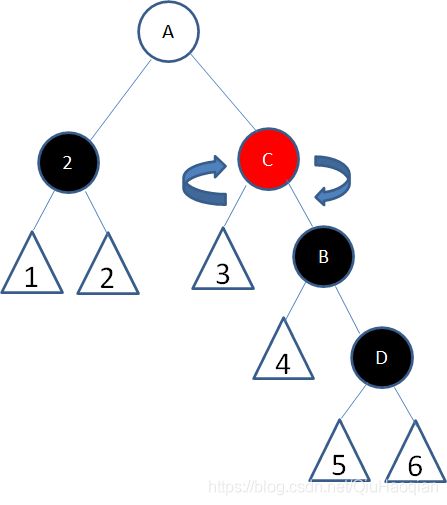
接下来结点B变为红色,结点C变为黑色:
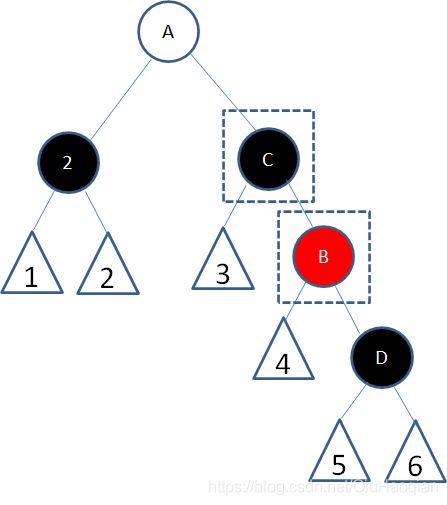
这样的变化转换成了子情况6。
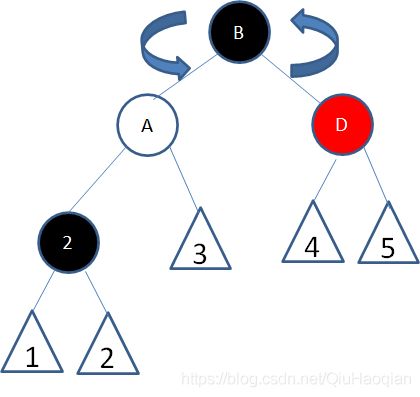
子情况6:结点2的父结点随意,兄弟结点B是黑色右孩子,右侄子结点是红色:
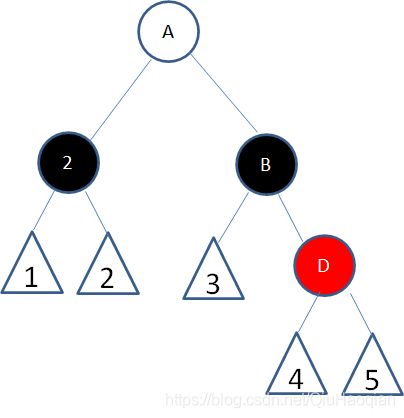
首先以结点2的父结点A为轴左旋:
接下来让结点A和结点B的颜色交换,并且结点D变为黑色:
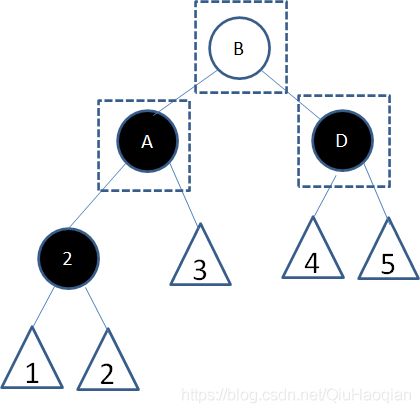
这样是否解决了问题呢?
经过结点2的路径由(随意+黑)变成了(随意+黑+黑),补充了一个黑色结点;
经过结点D的路径由(随意+黑+红)变成了(随意+黑),黑色结点并没有减少。
所以,这时候重新符合了红黑树的规则。
下边给出一个实际案例
下面这颗红黑树,待删除的是结点17:
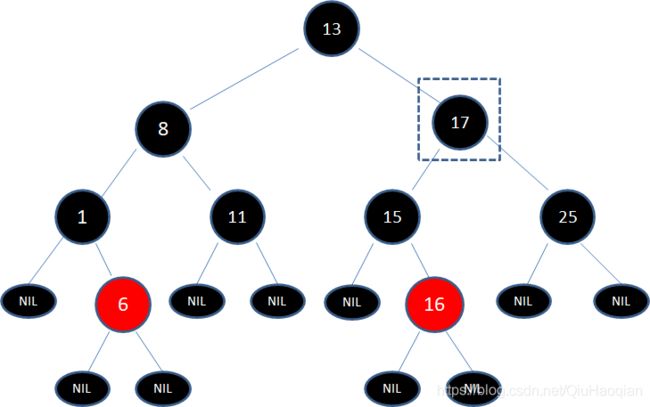
第一步: 结点17有两个孩子,子树当中仅大于17的结点是25,所以把结点25复制到17位置,保持17y原来的颜色–黑色:
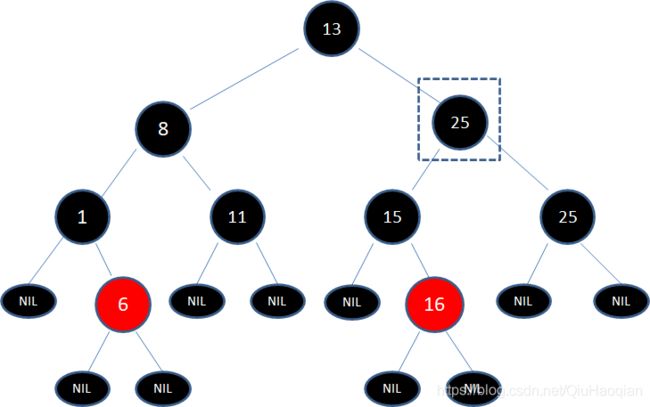
接下来,需要删除原本的结点25
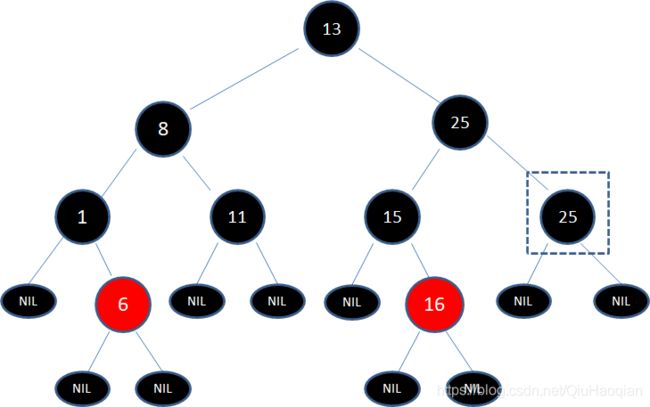
这个情况对应于 第二步的情况3,即待删除结点是黑色,子结点是空叶子结点。于是删除框中结点25,进入第三步的情况。
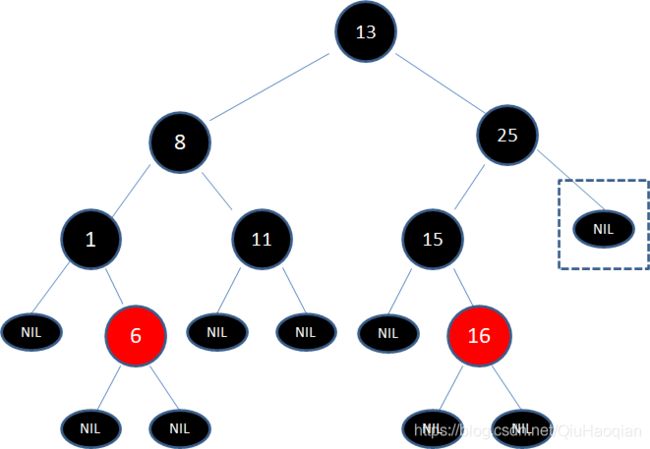
此时,框中的结点虽然是空叶子结点,但仍然可以用于判断局面,当前局面符合 第三步的子情况5 的镜像:

该情况 与 第三步的子情况5 的对比
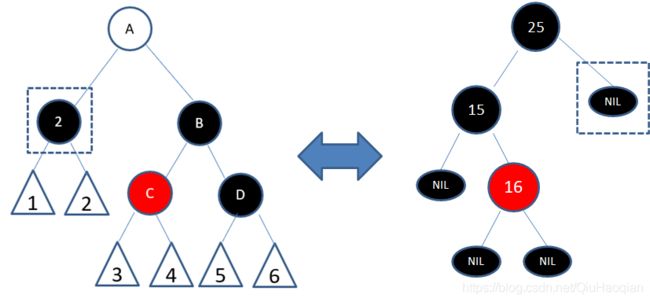
于是通过左旋和变色,把子树转换成情况6的镜像:
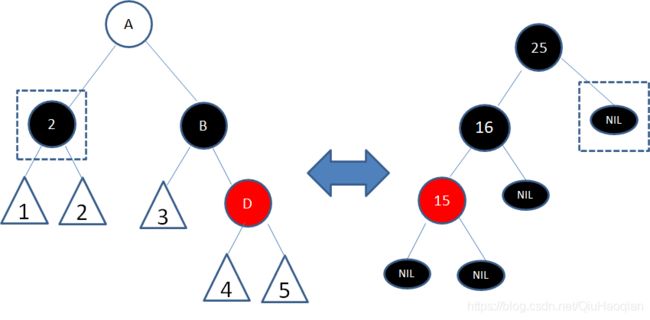
再经过右旋、变色,子树最终成为了下面的样子:
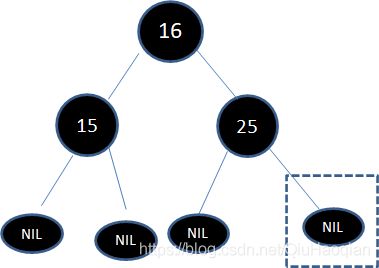
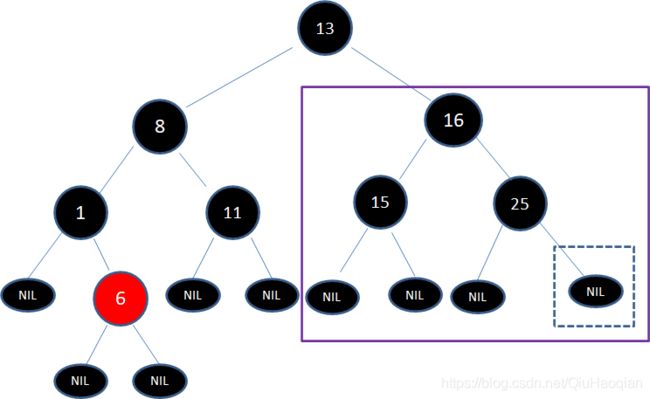
这样一来,整颗二叉树又重新符合了红黑树的规则。
4.5 应用场景
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是 O(logn),效率非常之高。
例如,Java 集合中的 TreeSet 和 TreeMap,C++ STL 中的 set、map,以及 Linux 虚拟内存的管理,都是通过红黑树去实现的。