高纬度矩阵乘法的意义

最近看到对比学习里面的loss，是比较复杂的，对于里面的矩阵乘法的意义不是很懂，自己试验了一下。

假设一个tensor（batchsize，length，feature），记为（B,L,F）。

如果用（B，L，F）和（B，F，L）相乘。

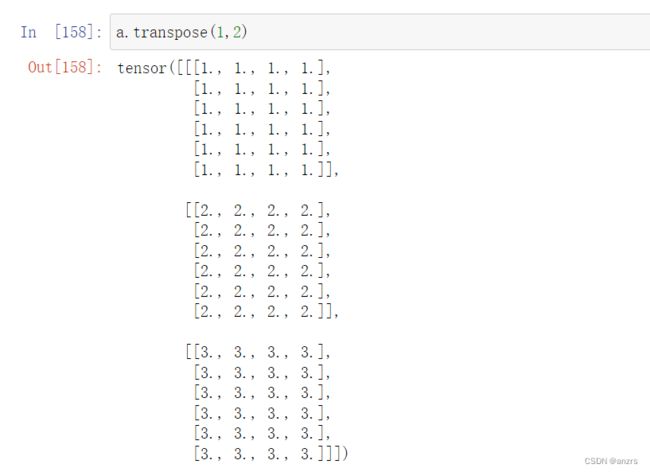
我们试验一下，也就是第一个batch全是1，第二个batch全是2，第三个batch全是3.

 那么transpose后，是这样的。

 对于这两个矩阵相乘，

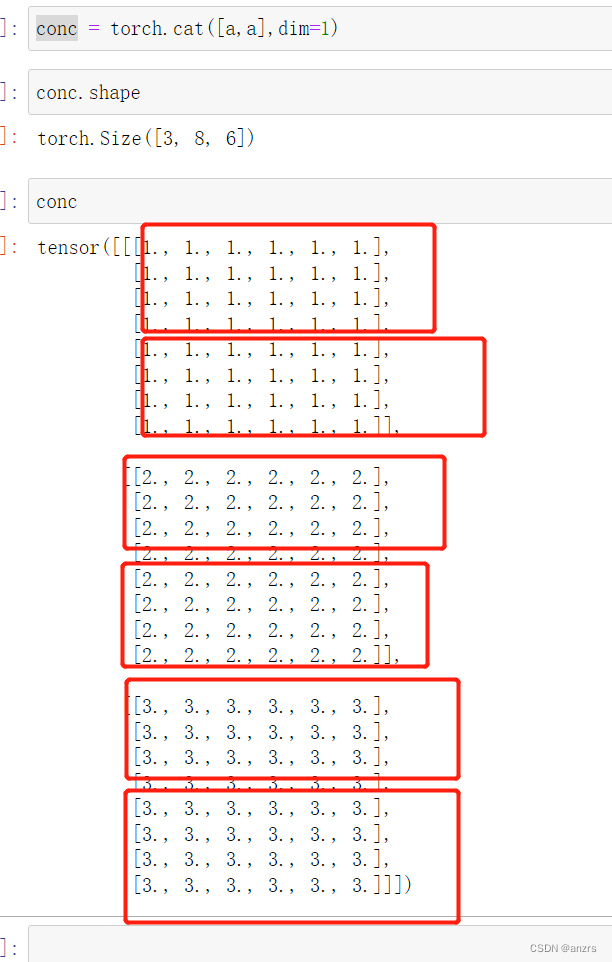
就相当于（batchsize，length，feature）乘（batchsize，feature，length）。我们看看乘出来的结果。

很明显乘法出来后的尺寸是，（batchsize，length，length），但是看里面的元素，第一个维度里面

第一个维度里面全是6，这说明做乘法的时候只是第一个维度和第一个维度做乘法。

好比这个batchsize是8，也就是说第一个batchsize里面的向量自己的乘积是得出来的第一个维度的值。固定batchsize不动，后面的做乘法，得出来的是自己的关系。

 

 

试一下对比学习的loss。

我们假设z1,是（3,4,6）的。这里的z1和z2是通过一个net的两个不同表征，差别很小。

 （1）cat后，成了这样，也就是把每个batch的相同位置的东西放在了一起，也就是说好比，第一个batch的x1，和第二个batch的x1_,放在了一起。

 （2）然后做这个sim，也就是这里的相似性。我们看看怎么做乘法做出来的。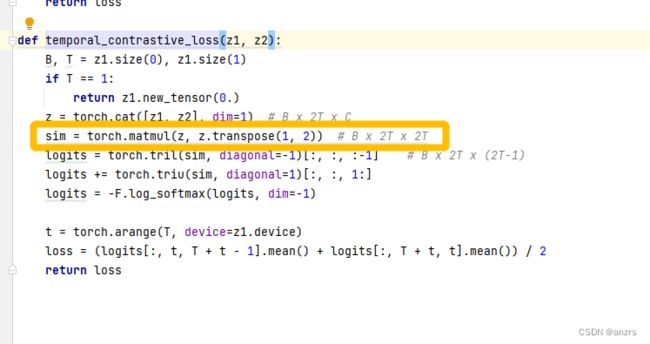

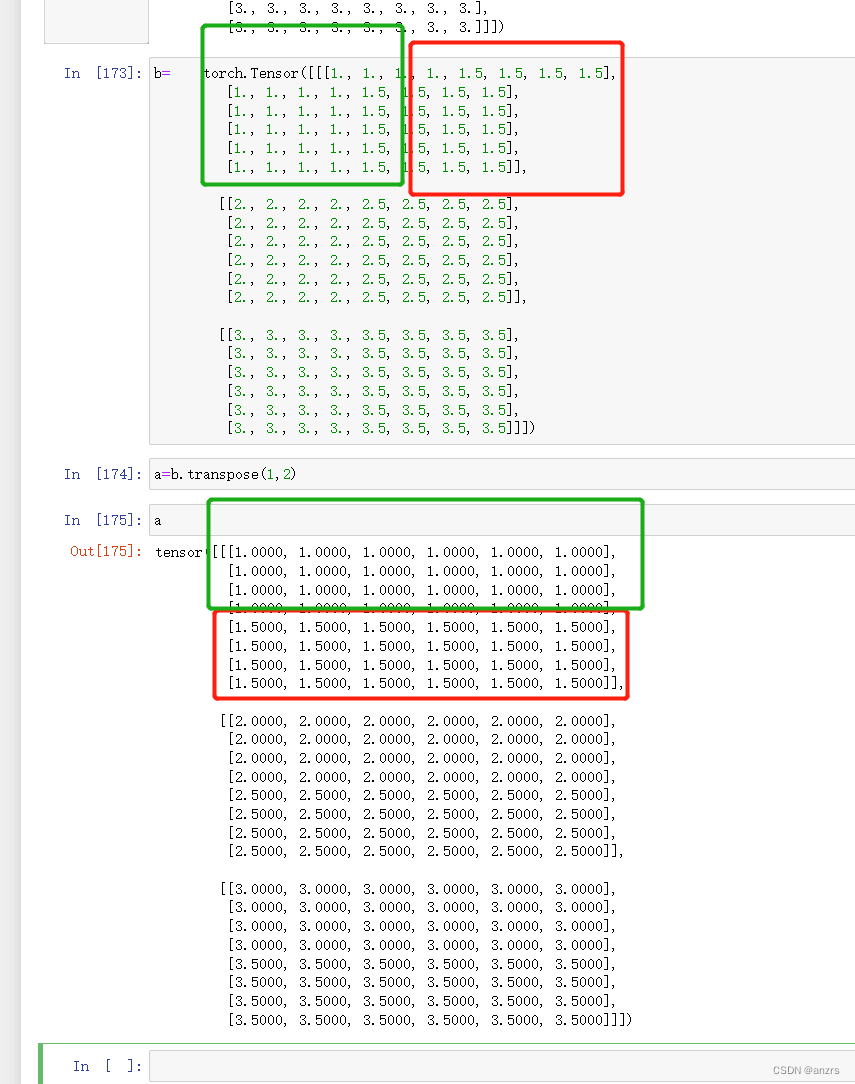
做了transpose后的就是红色的还是红色的，

 为了模拟文章的实际意义，我们用细微的区别来代替，也就是1变成了1.5，2变成了2.5.

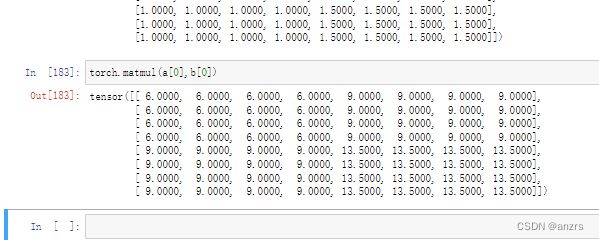
 然后另ab相乘，也就是（batchsize，8, 6）×（batchsize，6, 8）。

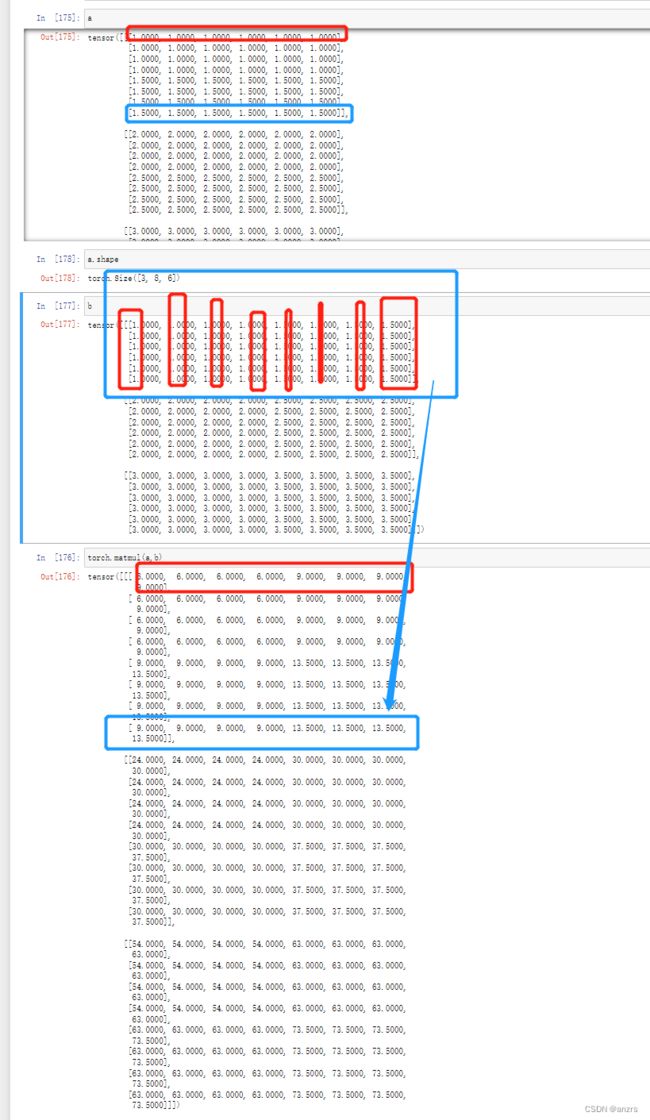
 从乘积的结果，可以看出来，好像下面这个乘积最里面的数字，都是上面的第一个维度盛出来的。确认一下，是这个结果。也就是说，

（batchsize，length，feature）x (batchsize,feature , length)->(batchsize,length,length),盛出来的一个batchsize，是维度对应的。

也就是说，如果是（3,5,4）x（3,4,5）-》（3,5,5），这个乘出来的（1,5,5）有三个，而且每一个只和对应维度才有关系。也就是说，第一个（1,5,4）x（1,4,5）-》（1,5,5）就是乘出来的第一个维度的。