一、实验目的
Ø 熟悉 掌握启发式搜索算法 A* 及其可采纳性
二、实验内容
编写程序实现 8 数码和 15 数码问题,采用至少两种估价函数
分析估价函数求解问题时候的效率差别, 分析 估价函数对搜索算法的影响
三、解题思路
3.1解题思路
1)首先定义节点的数据结构,包含路径代价f,当前节点状态即各个格子中的值用p[N][N]表示(N为自己定义的值,若为八数码问题,则N为3,若为十五数码问题,则N为4),其父亲节点father,深度d(方便计算路径代价),还有四个方向的变量,用来判断有哪个方向不需要进行拓展,例如某一节点其父亲节点经过向下移动得到此节点,则此节点就不需要再向上移动进行拓展了。
2)建立open表和close表并将初始节点放入open表中,我是用vector容器实现的这两个表。
3)接下来进行搜索循环,首先取出open表表首节点n
4)再对n节点进行搜索扩展(在拓展时同时判断是否找到目标节点),计算路径代价,并将新拓展出的节点的,如果扩展出的节点是全新的节点,则直接加入到open表中,如果拓展出的节点已经出现在open表中(假设老节点即出现在open表中的节点为n1,新节点为n2),则比较n2和n1的路径代价,如果n2>n1,则维持不变,如果n2
5)将首节点从open表中删除并添加到close表中
6)按照路径代价从小到大的顺序重新排列open表中
7)如果没有找到,则重复这个搜索循环的过程,如果找到了,则进行输出
四、实验代码:
#include
#define N 3
//#define N 4
#include
#include
using namespace std;
/*测试用例
八数码:1 0 3
2 7 5
6 8 4
十五数码: 1 2 0 4
12 13 14 5
11 3 15 6
10 9 8 7
*/
int target[N][N]={{1,2,3},{8,0,4},{7,6,5}};//八数码问题的目标
//int target[N][N]={{1,2,3,4},{12,13,14,5},{11,0,15,6},{10,9,8,7}};//十五数码问题的目标
struct Node{//节点的结构体
int f;//存放路径代价
int p[N][N];//存放当前状态
Node *father;//存放父亲节点
int d;//深度
int up;//记录是由那个移动操作得到的此节点,之后便不再扩展
int down;
int left;
int right;
};
Node *s=new Node;//初始节点s
vectoropen;//open表
vectorclose;//close表
int flag=0;//判断有没有找到的标志量
int pj(Node *t){//评价函数1
int i,j;
int h=0;//启发式值
for(i=0;ip[i][j]!=target[i][j]){
h++;
}
}
}
return h;
}
//int pj(Node *t){//评价函数2
// int i,j;
// int m,n;
// int flag2=0;
// int h=0;//启发式值
// for(m=0;mp[i][j]==a){
// h+=abs(i-m)+abs(j-n);
// flag2=1;
// }
// if(flag2==1){
// break;
// }
// }
// if(flag2==1){
// break;
// }
// }
// }
// }
// return h;
//}
bool same(Node *t,Node *a){//判断是否相同
int i,j;
for(i=0;ip[i][j]!=a->p[i][j]){
return false;
}
}
}
return true;
}
int ifopen(Node *t){//判断是否在open表里,是则返回在open表的序号,不是则返回-1
int i;
for(i=0;iff;
}
void scNode(Node *n){
int i,j;
cout<<" ";
for(i=0;ip[i][j]);
}
cout<ans;
Node *a=open[open.size()];//找到的目标节点必在open表最后一位
ans.push_back(a);
a=a->father;
while(same(a,s)==false){
ans.push_back(a);
a=a->father;
}
reverse(ans.begin(),ans.end());//将ans反转
int i;
for(i=0;ip[a][b]==0){
x=a;
y=b;
flag0=1;
break;
}
}
if(flag0==1){
break;
}
}
if(x!=0&&n->up){//可以向上移
// cout<<"上"<p[i][j]=n->p[i][j];
}
}
//进行移动
t->p[x][y]=t->p[x-1][y];
t->p[x-1][y]=0;
t->father=n;
t->up=1;
t->down=0;
t->left=1;
t->right=1;
t->d=n->d+1;
t->f=pj(t)+t->d;
if(pj(t)==0){//说明找到了目标节点
flag=1;
}
int a=ifopen(t);//判断是否出现在open表里
int c=ifclose(t);//判断是否出现在close表里
if(a!=-1){//如果出现在open表里
Node *b=open[a];
if(b->f>t->f){
b->f=t->f;
b->father=n;
b->d=t->d;
b->down=t->down;
b->up=t->up;
b->left=t->left;
b->right=t->right;
}
}else if(c!=-1){//如果出现在close表里
Node *e=close[c];
if(e->f>t->f){
e->f=t->f;
e->father=n;
e->d=t->d;
e->down=t->down;
e->up=t->up;
e->left=t->left;
e->right=t->right;
deletefromclose(c);//将此节点从close表中删去
open.push_back(e);//加入到open表中
}
}else{//全新节点
open.push_back(t);//加入到open表中
}
}
if(x!=N-1&&n->down){//可以向下移
// cout<<"下"<p[i][j]=n->p[i][j];
}
}
//进行移动
t->p[x][y]=t->p[x+1][y];
t->p[x+1][y]=0;
t->father=n;
t->up=0;
t->down=1;
t->left=1;
t->right=1;
t->d=n->d+1;
t->f=pj(t)+t->d;
if(pj(t)==0){//说明找到了目标节点
flag=1;
}
int a=ifopen(t);//判断是否出现在open表里
int c=ifclose(t);//判断是否出现在close表里
if(a!=-1){//如果出现在open表里
Node *b=open[a];
if(b->f>t->f){
b->f=t->f;
b->father=n;
b->d=t->d;
b->down=t->down;
b->up=t->up;
b->left=t->left;
b->right=t->right;
}
}else if(c!=-1){//如果出现在close表里
Node *e=close[c];
if(e->f>t->f){
e->f=t->f;
e->father=n;
e->d=t->d;
e->down=t->down;
e->up=t->up;
e->left=t->left;
e->right=t->right;
deletefromclose(c);//将此节点从close表中删去
open.push_back(e);//加入到open表中
}
}else{//全新节点
open.push_back(t);//加入到open表中
}
}
if(y!=N-1&&n->right){//可以向右移
// cout<<"右"<p[i][j]=n->p[i][j];
}
}
//进行移动
t->p[x][y]=t->p[x][y+1];
t->p[x][y+1]=0;
t->father=n;
t->up=1;
t->down=1;
t->left=0;
t->right=1;
t->d=n->d+1;
t->f=pj(t)+t->d;
if(pj(t)==0){//说明找到了目标节点
flag=1;
}
int a=ifopen(t);//判断是否出现在open表里
int c=ifclose(t);//判断是否出现在close表里
if(a!=-1){//如果出现在open表里
Node *b=open[a];
if(b->f>t->f){
b->f=t->f;
b->father=n;
b->d=t->d;
b->down=t->down;
b->up=t->up;
b->left=t->left;
b->right=t->right;
}
}else if(c!=-1){//如果出现在close表里
Node *e=close[c];
if(e->f>t->f){
e->f=t->f;
e->father=n;
e->d=t->d;
e->down=t->down;
e->up=t->up;
e->left=t->left;
e->right=t->right;
deletefromclose(c);//将此节点从close表中删去
open.push_back(e);//加入到open表中
}
}else{//全新节点
open.push_back(t);//加入到open表中
}
}
if(y!=0&&n->left){//可以向左移
// cout<<"左"<p[i][j]=n->p[i][j];
}
}
//进行移动
t->p[x][y]=t->p[x][y-1];
t->p[x][y-1]=0;
t->father=n;
t->up=1;
t->down=1;
t->left=1;
t->right=0;
t->d=n->d+1;
t->f=pj(t)+t->d;
if(pj(t)==0){//说明找到了目标节点
flag=1;
}
int a=ifopen(t);//判断是否出现在open表里
int c=ifclose(t);//判断是否出现在close表里
if(a!=-1){//如果出现在open表里
Node *b=open[a];
if(b->f>t->f){
b->f=t->f;
b->father=n;
b->d=t->d;
b->down=t->down;
b->up=t->up;
b->left=t->left;
b->right=t->right;
}
}else if(c!=-1){//如果出现在close表里
Node *e=close[c];
if(e->f>t->f){
e->f=t->f;
e->father=n;
e->d=t->d;
e->down=t->down;
e->up=t->up;
e->left=t->left;
e->right=t->right;
deletefromclose(c);//将此节点从close表中删去
open.push_back(e);//加入到open表中
}
}else{//全新节点
open.push_back(t);//加入到open表中
}
}
}
void A(Node *s){
int i,j;
while(1){
Node *n=open[0];//取出open表表首节点n
kzjd(n);
deletefromopen();//将首节点删除
close.push_back(n);//将此节点加入到close表中
sort(open.begin(),open.end(),cmp);//利用sort函数排序open表
if(flag==1){//如果找到了
break;
}
}
sc();//进行输出
}
int main(){
cout<<"请输入初始状态"<>s->p[i][j];
}
}
cout<<" ";
s->f=0;
s->father=NULL;
s->d=0;
s->up=1;
s->down=1;
s->left=1;
s->right=1;
open.push_back(s);
A(s);
cout<<"总拓展节点"<
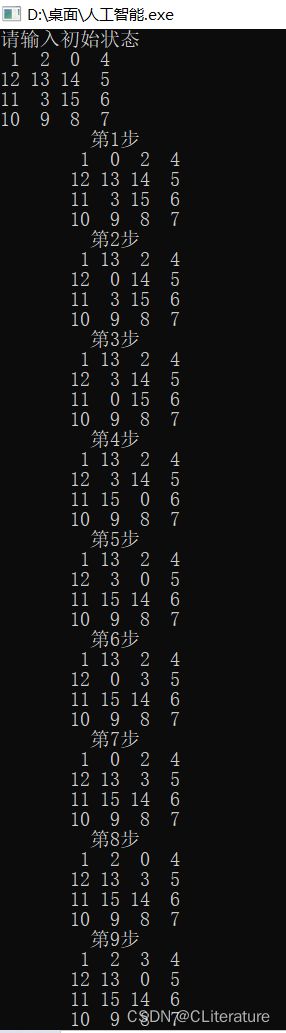
五、测试数据:
八数码问题:1 0 3
2 7 5
6 8 4
十五数码问题:1 2 0 4
12 13 14 5
11 3 15 6
10 9 8 7
六、输出结果:
八数码问题:
采用评价函数1:

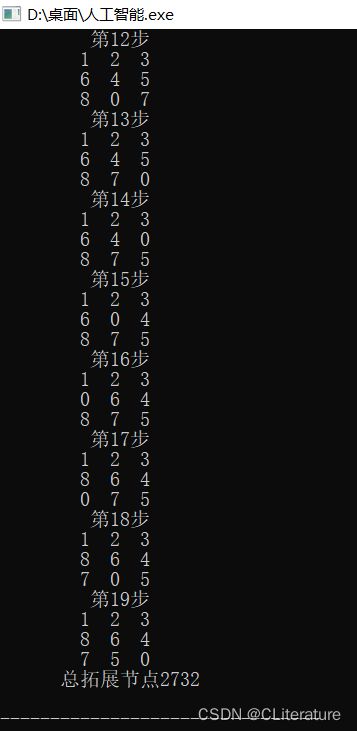
采用评价函数2:

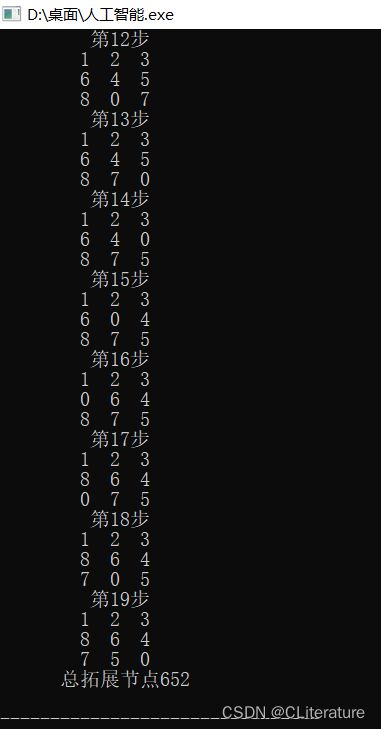
十五数码问题:
采用评价函数1:


采用评价函数2: