如何解释线性回归、逻辑回归、softmax回归?
Reference:
https://www.cnblogs.com/eilearn/p/8990073.html
回归是什么意思?
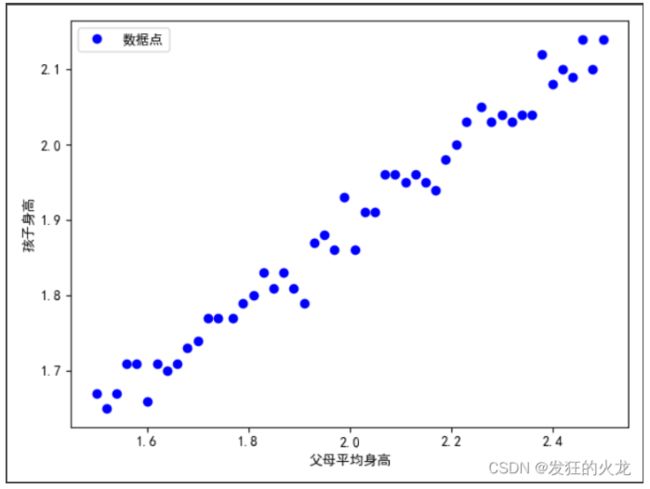
回归=预测,高尔顿使用最小二乘法研究父母与孩子身高时发现,孩子有回归至平均身高的倾向。高尔顿当时拟合了父母平均身高x和子女平均身高y的经验方程:Y= 0. 8567+0. 516X (单位为米)。可以看到,父代身高每增加一个单位,其成年子女的平均身高只增加0.516个单位,“回归”到正常人平均身高(由下图形化展示可以看出,父母高孩子相对矮,父母矮孩子相对高),因此将找到Y= 0. 8567+0. 516X 函数所使用的方法命名为线性回归。因此回归其实就是通过父母升高去预测子女身高。
如何解释线性回归?
线性:一条直线或线段。(Y= 0. 8567+0. 516X是线性的)
高尔顿使用最小二乘法研究父母与孩子身高时发现,孩子有回归至平均身高的倾向。高尔顿当时拟合了父母平均身高x和子女平均身高y的经验方程:Y= 0. 8567+0. 516X (单位为米)。可以看到,父代身高每增加一个单位,其成年子女的平均身高只增加0.516个单位,“回归”到正常人平均身高(由下图形化展示可以看出,父母高孩子相对矮,父母矮孩子相对高),因此将找到Y= 0. 8567+0. 516*X 函数所使用的方法命名为线性回归。
回归:预测
线性回归是一种预测方法。就是构建一条线段(线性函数),根据已知输入数据去预测输出数据,比如根据父母身高预测子女身高。
题目:已知50对数据(x0:父母平均身高,y0孩子身高),使用线性回归的方法求一个线性函数反应父母平均身高与与孩子身高的映射关系。(说白了就是找一条直线函数y = kx+b,能够反映父母身高与孩子身高数据的规律)
x0 ([1.5 , 1.52, 1.54, 1.56, 1.58, 1.6 , 1.62, 1.64, 1.66, 1.68, 1.7 ,
1.72, 1.74, 1.77, 1.79, 1.81, 1.83, 1.85, 1.87, 1.89, 1.91, 1.93,
1.95, 1.97, 1.99, 2.01, 2.03, 2.05, 2.07, 2.09, 2.11, 2.13, 2.15,
2.17, 2.19, 2.21, 2.23, 2.26, 2.28, 2.3 , 2.32, 2.34, 2.36, 2.38,
2.4 , 2.42, 2.44, 2.46, 2.48, 2.5 ])
y0 ([1.67, 1.65, 1.67, 1.71, 1.71, 1.66, 1.71, 1.7 , 1.71, 1.73, 1.74,
1.77, 1.77, 1.77, 1.79, 1.8 , 1.83, 1.81, 1.83, 1.81, 1.79, 1.87,
1.88, 1.86, 1.93, 1.86, 1.91, 1.91, 1.96, 1.96, 1.95, 1.96, 1.95,
1.94, 1.98, 2. , 2.03, 2.05, 2.03, 2.04, 2.03, 2.04, 2.04, 2.12,
2.08, 2.1 , 2.09, 2.14, 2.1 , 2.14])
图形化展示
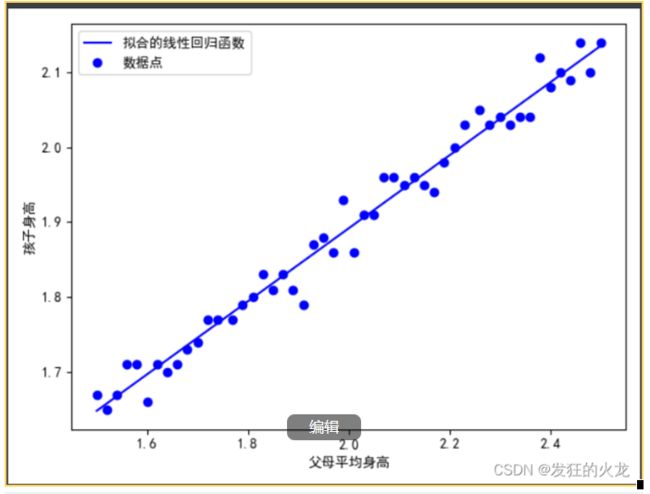
线性回归方法:使用最小二乘法求这个函数最合适的参数值,这里我试图使用一次函数拟合数据,设函数为y=wx+b,w、b就是我需要求的参数,结果如图所示:
python代码
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
# 数据x0:父母平均身高 y0:孩子身高
x0 = np.array([1.5, 1.52, 1.54, 1.56, 1.58, 1.6, 1.62, 1.64, 1.66, 1.68, 1.7,
1.72, 1.74, 1.77, 1.79, 1.81, 1.83, 1.85, 1.87, 1.89, 1.91, 1.93,
1.95, 1.97, 1.99, 2.01, 2.03, 2.05, 2.07, 2.09, 2.11, 2.13, 2.15,
2.17, 2.19, 2.21, 2.23, 2.26, 2.28, 2.3, 2.32, 2.34, 2.36, 2.38,
2.4, 2.42, 2.44, 2.46, 2.48, 2.5]
)
y0 = np.array([1.67, 1.65, 1.67, 1.71, 1.71, 1.66, 1.71, 1.7, 1.71, 1.73, 1.74,
1.77, 1.77, 1.77, 1.79, 1.8, 1.83, 1.81, 1.83, 1.81, 1.79, 1.87,
1.88, 1.86, 1.93, 1.86, 1.91, 1.91, 1.96, 1.96, 1.95, 1.96, 1.95,
1.94, 1.98, 2., 2.03, 2.05, 2.03, 2.04, 2.03, 2.04, 2.04, 2.12,
2.08, 2.1, 2.09, 2.14, 2.1, 2.14]
)
np.random.seed(0) # 随机数种子
n = int(input("输入拟合函数次数(整数):"))
w_b = np.around(np.random.randn(n), 2) # 随机生成多项式参数,w_b拟合函数参数array([1.76405235, 0.40015721])
# **计算误差
def residuals_func(w_b, x, y):
# f = np.poly1d(p) polyid是多项式函数,若n=1,w_b=1.76,f(x)=p=1.76。若n=2,w_b=[1.76 0.4],f(x)=1.76x+0.4。
# 若n=3,w_b=[1.76 0.4 0.98],f(x)=1.76x^2+0.4x+0.98等等......
# np.poly1d(w_b)(x) = f(x)
ret = np.poly1d(w_b)(x) - y
return ret
plsq = leastsq(residuals_func, w_b, args=(x0, y0)) # 最小二乘法黑箱计算,参数为(误差函数,误差函数的参数,样本点) 目的:调整w_b的数据,拟合数据点
# 绘制
plt.xlabel('父母平均身高')
plt.ylabel('孩子身高')
plt.plot(x0, np.poly1d(plsq[0])(x0), c='b', label='拟合的线性回归函数')
# plt.plot(x0, np.poly1d(w_b)(x0), c='b', label='拟合的线性回归函数')
plt.plot(x0, y0, 'bo', label='数据点')
plt.legend(loc='best') # 如果画图中有加lable,记得加上plt.legend(loc='best')
plt.show()
总结:线性回归是一种得到数据之间关系的方法。这种关系由一个确定的函数表示,如父母平均身高与孩子身高采用线性回归方法后得到y=1.76x+0.4
附录:
函数:在数学中为两不为空集的集合间的一种对应关系。例子:实数x对应x2 = 函数 = (f(x) = x2),函数的概念并不局限于数之间的映射关系。例子:Captital(U.K.) = London
维基百科
线性回归(英语:linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
回归分析(英语:Regression Analysis)是一种统计学上分析数据的方法,目的在于了解两个或多个变量间是否相关、相关方向与强度,并建立数学模型以便观察特定变量来预测研究者感兴趣的变量。
如何解释逻辑回归?
目的:从训练数据特征学习出一个0/1分类模型,离散型输出。
如何解释Softmax回归模型?
当多分类问题时,logistic推广为softmax.