基于Python实现的机器人自动走迷宫

资源下载地址：https://download.csdn.net/download/sheziqiong/85631466

机器人自动走迷宫

一 题目背景

1.1 实验题目

在本实验中，要求分别使用基础搜索算法和 Deep QLearning 算法，完成机器人自动走迷宫。

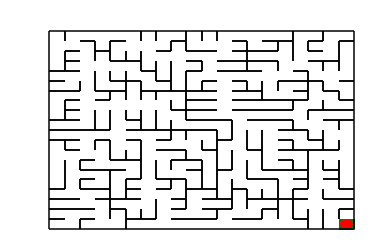
图1 地图（size10）

如上图所示，左上角的红色椭圆既是起点也是机器人的初始位置，右下角的绿色方块是出口。

游戏规则为：从起点开始，通过错综复杂的迷宫，到达目标点(出口)。

• 在任一位置可执行动作包括：向上走 'u'、向右走 'r'、向下走 'd'、向左走 'l'。

• 执行不同的动作后，根据不同的情况会获得不同的奖励，具体而言，有以下几种情况。

  • 撞墙
  • 走到出口
  • 其余情况

• 需要您分别实现基于基础搜索算法和 Deep QLearning 算法的机器人，使机器人自动走到迷宫的出口。

1.2 实验要求

• 使用 Python 语言。
• 使用基础搜索算法完成机器人走迷宫。
• 使用 Deep QLearning 算法完成机器人走迷宫。
• 算法部分需要自己实现，不能使用现成的包、工具或者接口。

1.3 实验使用重要python包

import os
import random
import numpy as np
import torch

二 迷宫介绍

通过迷宫类 Maze 可以随机创建一个迷宫。

1. 使用 Maze(maze_size=size) 来随机生成一个 size * size 大小的迷宫。
2. 使用 print() 函数可以输出迷宫的 size 以及画出迷宫图
3. 红色的圆是机器人初始位置
4. 绿色的方块是迷宫的出口位置

图2 gif地图（size10）

Maze 类中重要的成员方法如下：

1. sense_robot() ：获取机器人在迷宫中目前的位置。

return：机器人在迷宫中目前的位置。

2. move_robot(direction) ：根据输入方向移动默认机器人，若方向不合法则返回错误信息。

direction：移动方向, 如:“u”, 合法值为： [‘u’, ‘r’, ‘d’, ‘l’]

return：执行动作的奖励值

3. can_move_actions(position)：获取当前机器人可以移动的方向

position：迷宫中任一处的坐标点

return：该点可执行的动作，如：[‘u’,‘r’,‘d’]

4. is_hit_wall(self, location, direction)：判断该移动方向是否撞墙

location, direction：当前位置和要移动的方向，如(0,0) , “u”

return：True(撞墙) / False(不撞墙)

5. draw_maze()：画出当前的迷宫

三 算法介绍

3.1 深度优先算法

算法具体步骤：

• 选取图中某一顶点$V_i$为出发点，访问并标记该顶点；

• 以Vi为当前顶点，依次搜索$V_i$的每个邻接点$V_j$，若$V_j$未被访问过，则访问和标记邻接点$V_j$，若$V_j$已被访问过，则搜索$V_i$的下一个邻接点；

• 以$V_j$为当前顶点，重复上一步骤），直到图中和$V_i$有路径相通的顶点都被访问为止；

• 若图中尚有顶点未被访问过（非连通的情况下），则可任取图中的一个未被访问的顶点作为出发点，重复上述过程，直至图中所有顶点都被访问。

时间复杂度：

查找每个顶点的邻接点所需时间为$O(n^2)$，n为顶点数，算法的时间复杂度为$O(n^2)$

3.2 强化学习QLearning算法

Q-Learning 是一个值迭代（Value Iteration）算法。与策略迭代（Policy Iteration）算法不同，值迭代算法会计算每个”状态“或是”状态-动作“的值（Value）或是效用（Utility），然后在执行动作的时候，会设法最大化这个值。 因此，对每个状态值的准确估计，是值迭代算法的核心。通常会考虑最大化动作的长期奖励，即不仅考虑当前动作带来的奖励，还会考虑动作长远的奖励。

3.2.1 Q值计算与迭代

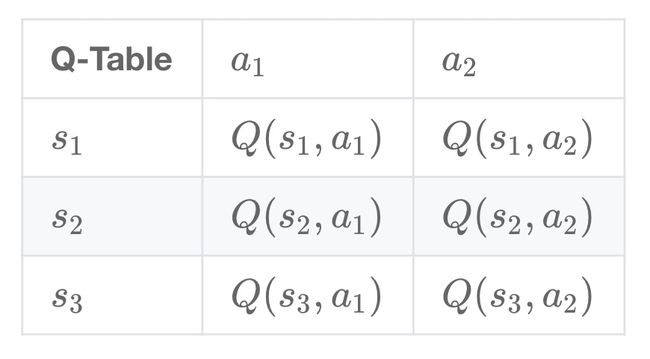
Q-learning 算法将状态（state）和动作（action）构建成一张 Q_table 表来存储 Q 值，Q 表的行代表状态（state），列代表动作（action）：

在 Q-Learning 算法中，将这个长期奖励记为 Q 值，其中会考虑每个 ”状态-动作“ 的 Q 值，具体而言，它的计算公式为：
$$Q(s_t,a)=R_{t+1}+\gamma \times \underset{a}{\max }Q(a,s_{t+1})$$

也就是对于当前的“状态-动作” $(s_t,a)$，考虑执行动作 $a$ 后环境奖励 $R_{t+1}$，以及执行动作 $a$ 到达 $s_{t+1}$后，执行任意动作能够获得的最大的Q值 ${\max }_{a}Q(a,s_{t+1})$，$\gamma$ 为折扣因子。

计算得到新的 Q 值之后，一般会使用更为保守地更新 Q 表的方法，即引入松弛变量 $alpha$ ，按如下的公式进行更新，使得 Q 表的迭代变化更为平缓。
$$Q(s_t,a)=(1-\alpha )\times Q(s_t,a)+\alpha \times (R_{t+1}+\gamma \times \underset{a}{\max }Q(a,s_{t+1}))$$

3.2.2 机器人动作的选择

在强化学习中，探索-利用 问题是非常重要的问题。 具体来说，根据上面的定义，会尽可能地让机器人在每次选择最优的决策，来最大化长期奖励。但是这样做有如下的弊端：

1. 在初步的学习中，Q 值是不准确的，如果在这个时候都按照 Q 值来选择，那么会造成错误。
2. 学习一段时间后，机器人的路线会相对固定，则机器人无法对环境进行有效的探索。

因此需要一种办法，来解决如上的问题，增加机器人的探索。通常会使用 epsilon-greedy 算法：

1. 在机器人选择动作的时候，以一部分的概率随机选择动作，以一部分的概率按照最优的 Q 值选择动作。
2. 同时，这个选择随机动作的概率应当随着训练的过程逐步减小。

3.2.3 Q-Learning 算法的学习过程

3.2.4 Robot 类

在本作业中提供了 QRobot 类，其中实现了 Q 表迭代和机器人动作的选择策略，可通过 from QRobot import QRobot 导入使用。

QRobot 类的核心成员方法

1. sense_state()：获取当前机器人所处位置

return：机器人所处的位置坐标，如： (0, 0)

2. current_state_valid_actions()：获取当前机器人可以合法移动的动作

return：由当前合法动作组成的列表，如： [‘u’,‘r’]

3. train_update()：以训练状态，根据 QLearning 算法策略执行动作

return：当前选择的动作，以及执行当前动作获得的回报, 如： ‘u’, -1

4. test_update()：以测试状态，根据 QLearning 算法策略执行动作

return：当前选择的动作，以及执行当前动作获得的回报, 如：‘u’, -1

5. reset()

return：重置机器人在迷宫中的位置

3.2.5 Runner 类

QRobot 类实现了 QLearning 算法的 Q 值迭代和动作选择策略。在机器人自动走迷宫的训练过程中，需要不断的使用 QLearning 算法来迭代更新 Q 值表，以达到一个“最优”的状态，因此封装好了一个类 Runner 用于机器人的训练和可视化。可通过 from Runner import Runner 导入使用。

Runner 类的核心成员方法：

1. run_training(training_epoch, training_per_epoch=150): 训练机器人，不断更新 Q 表，并讲训练结果保存在成员变量 train_robot_record 中

training_epoch, training_per_epoch: 总共的训练次数、每次训练机器人最多移动的步数

2. run_testing()：测试机器人能否走出迷宫

3. generate_gif(filename)：将训练结果输出到指定的 gif 图片中

filename：合法的文件路径,文件名需以 .gif 为后缀

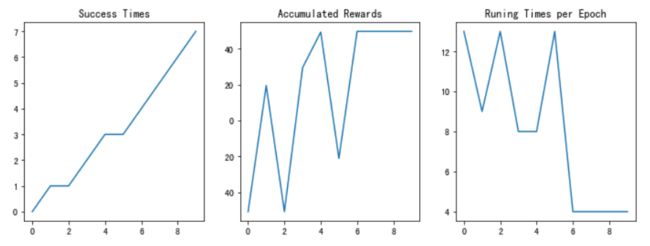
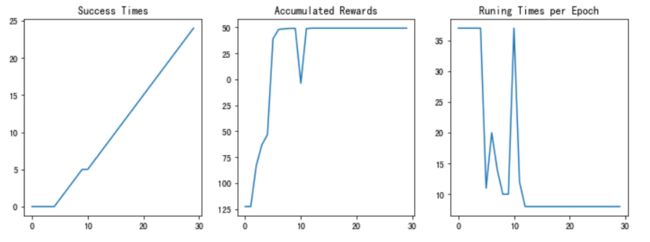
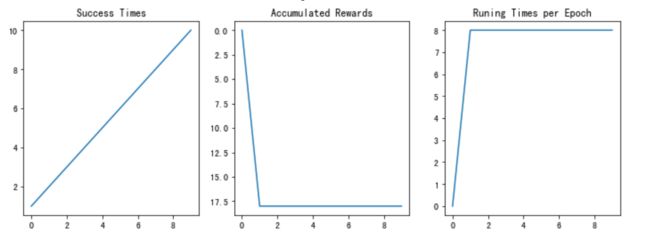
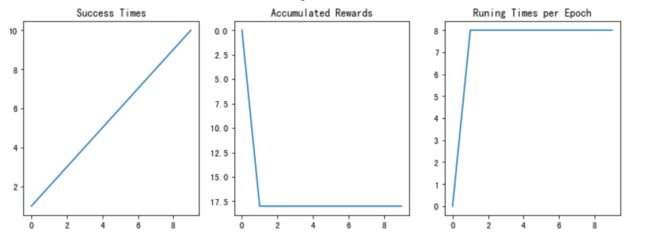
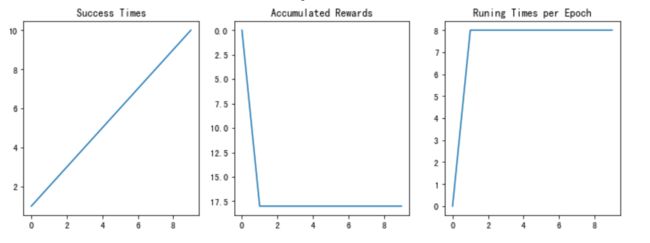
4. plot_results()：以图表展示训练过程中的指标：Success Times、Accumulated Rewards、Runing Times per Epoch

3.3 DQN

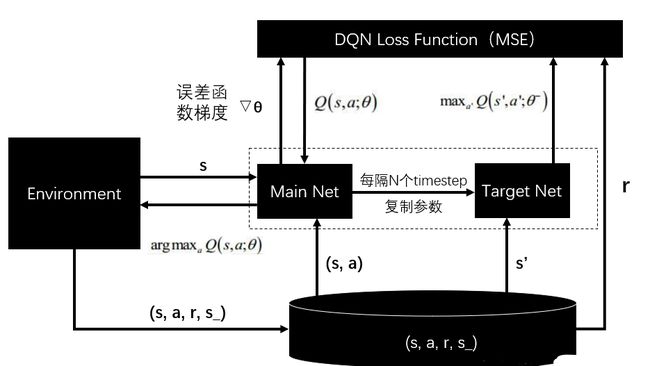
DQN 算法使用神经网络来近似值函数，算法框图如下。

在本次实验中，使用提供的神经网络来预计四个动作的评估分数，同时输出评估分数。

ReplayDataSet 类的核心成员方法

• add(self, state, action_index, reward, next_state, is_terminal) 添加一条训练数据

state: 当前机器人位置

action_index: 选择执行动作的索引

reward： 执行动作获得的回报

next_state：执行动作后机器人的位置

is_terminal：机器人是否到达了终止节点（到达终点或者撞墙）

• random_sample(self, batch_size)：从数据集中随机抽取固定batch_size的数据

batch_size: 整数，不允许超过数据集中数据的个数

• build_full_view(self, maze)：开启金手指，获取全图视野

maze: 以 Maze 类实例化的对象

四 求解结果

4.1 深度优先

编写深度优先搜索算法，并进行测试，通过使用堆栈的方式，来进行一层一层的迭代，最终搜索出路径。主要过程为，入口节点作为根节点，之后查看此节点是否被探索过且是否存在子节点，若满足条件则拓展该节点，将该节点的子节点按照先后顺序入栈。若探索到一个节点时，此节点不是终点且没有可以拓展的子节点，则将此点出栈操作，循环操作直到找到终点。

测试结果如下：

• 若maze_size=5，运行基础搜索算法，最终成果如下：

搜索出的路径： ['r', 'd', 'r', 'd', 'd', 'r', 'r', 'd']
恭喜你，到达了目标点
Maze of size (5, 5)

图3 基础搜索地图（size5）

• 若maze_size=10，运行基础搜索算法，最终成果如下：

搜索出的路径： ['r', 'r', 'r', 'r', 'r', 'r', 'r', 'd', 'r', 'd', 'd', 'd', 'r', 'd', 'd', 'd', 'l', 'd', 'd', 'r']
恭喜你，到达了目标点
Maze of size (10, 10)

图4 基础搜索地图（size10）

• 若maze_size=20，运行基础搜索算法，最终成果如下：

搜索出的路径： ['d', 'r', 'u', 'r', 'r', 'r', 'r', 'd', 'r', 'd', 'r', 'r', 'r', 'r', 'd', 'd', 'r', 'd', 'd', 'd', 'd', 'r', 'r', 'r', 'r', 'r', 'd', 'r', 'r', 'd', 'r', 'd', 'd', 'l', 'l', 'd', 'd', 'd', 'd', 'd', 'r', 'd', 'd', 'r']
恭喜你，到达了目标点
Maze of size (20, 20)

图5 基础搜索地图（size20）

部分代码如下：

def myDFS(maze):
        """
        对迷宫进行深度优先搜索
        :param maze: 待搜索的maze对象
        """
        start = maze.sense_robot()
        root = SearchTree(loc=start)
        queue = [root]  # 节点堆栈，用于层次遍历
        h, w, _ = maze.maze_data.shape
        is_visit_m = np.zeros((h, w), dtype=np.int)  # 标记迷宫的各个位置是否被访问过
        path = []  # 记录路径
        peek = 0
        while True:
            current_node = queue[peek]  # 栈顶元素作为当前节点
            #is_visit_m[current_node.loc] = 1  # 标记当前节点位置已访问
            if current_node.loc == maze.destination:  # 到达目标点
                path = back_propagation(current_node)
                break
            if current_node.is_leaf() and is_visit_m[current_node.loc] == 0:  # 如果该点存在叶子节点且未拓展
                is_visit_m[current_node.loc] = 1  # 标记该点已拓展
                child_number = expand(maze, is_visit_m, current_node)
                peek+=child_number  # 开展一些列入栈操作
                for child in current_node.children:
                    queue.append(child)  # 叶子节点入栈
            else:
                queue.pop(peek)  # 如果无路可走则出栈
                peek-=1
        return path

4.2 QLearning

在算法训练过程中，首先读取机器人当前位置，之后将当前状态加入Q值表中，如果表中已经存在当前状态则不需重复添加。之后，生成机器人的需要执行动作，并返回地图奖励值、查找机器人现阶段位置。接着再次检查并更新Q值表，衰减随机选取动作的可能性。

QLearning算法实现过程中，主要是对Q值表的计算更新进行了修改和调整，调整后的Q值表在运行时性能优秀，计算速度快且准确性、稳定性高。之后调节了随机选择动作可能性的衰减率。因为在测试过程中发现，如果衰减太慢的话会导致随机性太强，间接的减弱了奖励的作用，故最终通过调整，发现衰减率取0.5是一个较为优秀的且稳定的值。

部分代码如下：

    def train_update(self):
        """
        以训练状态选择动作，并更新相关参数
        :return :action, reward 如："u", -1
        """
        self.state = self.maze.sense_robot()  # 获取机器人当初所处迷宫位置

        # 检索Q表，如果当前状态不存在则添加进入Q表
        if self.state not in self.q_table:
            self.q_table[self.state] = {a: 0.0 for a in self.valid_action}

        action = random.choice(self.valid_action) if random.random() < self.epsilon else max(self.q_table[self.state], key=self.q_table[self.state].get)  # action为机器人选择的动作
        reward = self.maze.move_robot(action)  # 以给定的方向移动机器人,reward为迷宫返回的奖励值
        next_state = self.maze.sense_robot()  # 获取机器人执行指令后所处的位置

        # 检索Q表，如果当前的next_state不存在则添加进入Q表
        if next_state not in self.q_table:
            self.q_table[next_state] = {a: 0.0 for a in self.valid_action}

        # 更新 Q 值表
        current_r = self.q_table[self.state][action]
        update_r = reward + self.gamma * float(max(self.q_table[next_state].values()))
        self.q_table[self.state][action] = self.alpha * self.q_table[self.state][action] +(1 - self.alpha) * (update_r - current_r)

        self.epsilon *= 0.5  # 衰减随机选择动作的可能性

        return action, reward

测试结果如下：

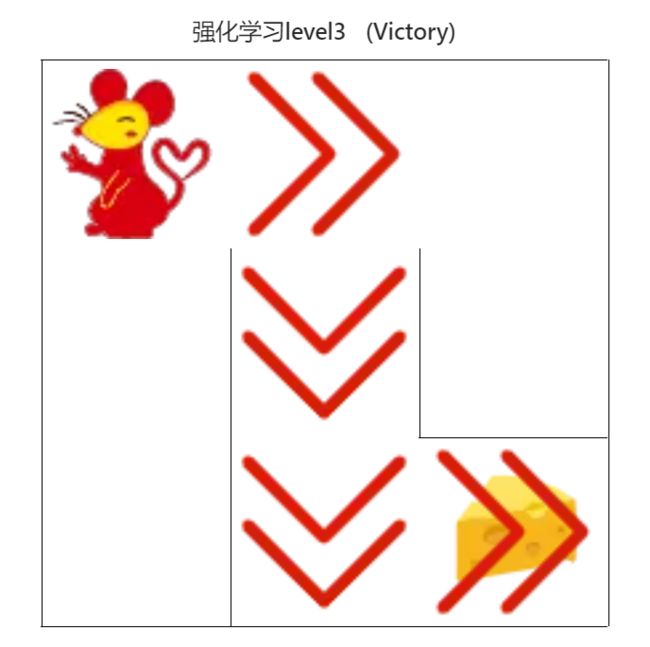
• 若maze_size=3，运行强化学习搜索算法，最终成果如下：

图6 强化学习搜索gif地图（size3）

图7 训练结果

• 若maze_size=5，运行强化学习搜索算法，最终成果如下：

图8 强化学习搜索gif地图（size5）

图9 训练结果

• 若maze_size=10，运行强化学习搜索算法，最终成果如下：

图10 强化学习搜索gif地图（size10）

图11 训练结果

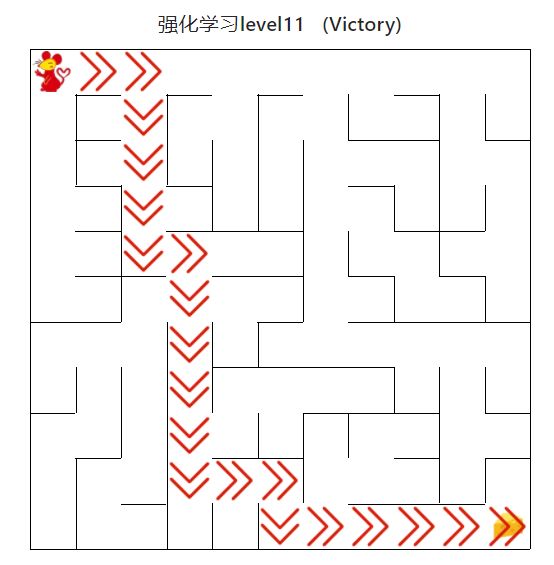
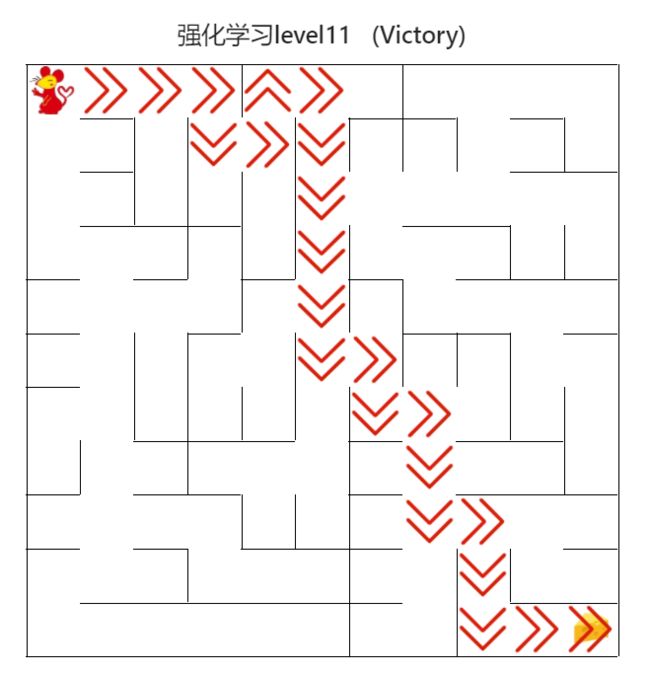
• 若maze_size=11，运行强化学习搜索算法，最终成果如下：

图12 强化学习搜索gif地图（size11）

图13 训练结果

经过测试，强化学习搜索算法可以快速给出走出迷宫的路径并且随着训练轮次增加，成功率也逐渐上升。当训练轮次足够时，最终后期准确率可以达到100%。

4.3 DQN

在Q-Learning 的基础上，使用神经网络来估计评估分数，用于决策之后的动作。只需在Q-Learning相应部分替换为神经网络的输出即可。

测试结果如下：

• 若maze_size=3，运行DQN算法，最终成果如下：

  

  图14 训练结果

• 若maze_size=5，运行DQN算法，最终成果如下：

  

  图15 训练结果

• 若maze_size=10，运行DQN算法，最终成果如下：

  

  图16 训练结果

4.4 提交结果测试

4.4.1 基础搜索算法测试

图17 基础搜索算法路径

用时0秒

4.4.2 强化学习算法（初级）

图18 强化学习算法（初级）

用时0秒

4.4.3 强化学习算法（中级）

图19 强化学习算法（中级）

用时0秒

4.4.4 强化学习算法（高级）

图20 强化学习算法（高级）

用时0秒

4.4.5 DQN算法（初级）

图21 DQN算法（初级）

用时2秒

4.4.6 DQN算法（中级）

图22 DQN算法（中级）

用时3秒

4.4.7 DQN算法（高级）

图23 DQN算法（高级）

资源下载地址：https://download.csdn.net/download/sheziqiong/85631466