【论文笔记+代码解读】《ATTENTION, LEARN TO SOLVE ROUTING PROBLEMS!》

介绍

本文提出了一种注意力层+强化学习的训练模型，以解决TSP、VRP、OP、PCTSP等路径问题。文章致力于使用相同的超参数，解决多种路径问题。文中采用了贪心算法作为基线，相较于值函数效果更好。

注意力模型

文中定义了Attention Model以解决TSP问题，针对其它问题，不需要改变模型，只需要修改输入、掩码、解码上下文等参量。模型采用编码-解码结构，编码器生成所有输入节点的嵌入，解码器依次生成输入节点的序列π。以下都以TSP问题举例：

编码器

本文中的编码器部分与Transformer架构中的编码器类似，但不使用位置编码。编码器结点输入维度是2，经过一个线性网络将特征维度扩展到128维；之后经过N个子层得到输出。其中，每个子层都是由一个8头注意力层和一个全连接层组成，每层都采用了残差连接，经过了批归一化得到输出。
输入：
x (batch_size, graph_size, embed_dim)
输出：
h (batch_size, graph_size, embed_dim)结点嵌入
h.mean (batch_size, embed_dim)图嵌入

*
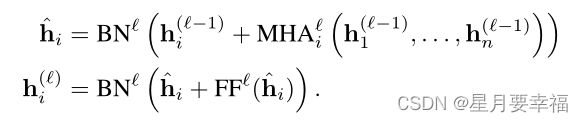结点编码类class GraphAttentionEncoder：*

class GraphAttentionEncoder(nn.Module):
    def __init__(
            self,
            n_heads,
            embed_dim,
            n_layers,
            node_dim=None,
            normalization='batch',
            feed_forward_hidden=512
    ):
        super(GraphAttentionEncoder, self).__init__()

        # To map input to embedding space
        self.init_embed = nn.Linear(node_dim, embed_dim) if node_dim is not None else None

        self.layers = nn.Sequential(*(
            MultiHeadAttentionLayer(n_heads, embed_dim, feed_forward_hidden, normalization)
            for _ in range(n_layers)
        ))

    def forward(self, x, mask=None):

        assert mask is None, "TODO mask not yet supported!"

        # Batch multiply to get initial embeddings of nodes
        h = self.init_embed(x.view(-1, x.size(-1))).view(*x.size()[:2], -1) if self.init_embed is not None else x

        h = self.layers(h)

        return (
            h,  # (batch_size, graph_size, embed_dim)
            h.mean(dim=1),  # average to get embedding of graph, (batch_size, embed_dim)
        )

子层MHA+FF class MultiHeadAttentionLayer:

class MultiHeadAttentionLayer(nn.Sequential):

    def __init__(
            self,
            n_heads,
            embed_dim,
            feed_forward_hidden=512,
            normalization='batch',
    ):
        super(MultiHeadAttentionLayer, self).__init__(
            SkipConnection(
                MultiHeadAttention(
                    n_heads,
                    input_dim=embed_dim,
                    embed_dim=embed_dim
                )
            ),
            Normalization(embed_dim, normalization),
            SkipConnection(
                nn.Sequential(
                    nn.Linear(embed_dim, feed_forward_hidden),
                    nn.ReLU(),
                    nn.Linear(feed_forward_hidden, embed_dim)
                ) if feed_forward_hidden > 0 else nn.Linear(embed_dim, embed_dim)
            ),
            Normalization(embed_dim, normalization)
        )

解码器

输出：
cost (batch_size) 总路径
_log_p (batch_size, graph_size) 结点输出概率和
pi (batch_size, graph_size) 游走序列
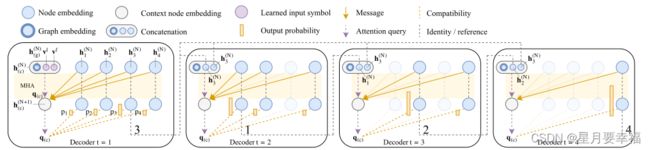
解码器是由两层attention层组成，先经过一层多头注意力层，再经过一层单头注意力层得到相关性分数logits。
结点经过编码器后进行解码，解码过程中使用了一个上下文结点c来表示解码上下文。上下文结点是由编码过程中得到的图嵌入、序列中第一个结点嵌入、序列中上一步添加的结点嵌入三者经过线性变换作为query，编码后的结点通过线性变换作为key、value：
特别的，选取第一个结点时，采用两个可学习的参数代替第一个结点和上一步结点。上下文结点嵌入定义如下：
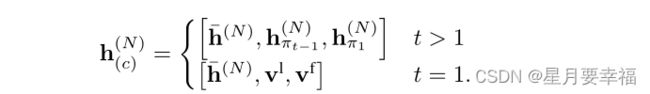这里的[ · · ]组合文中说是三个向量的连接，但是代码中不是这样，代码中是将图嵌入经过一个线性网络后与两个结点嵌入连接后经过线性网络相加得到：

query = fixed.context_node_projected + self.project_step_context(self._get_parallel_step_context(fixed.node_embeddings, state))

特别说明：两次注意力机制中的glimpse key、glimpse value、logit key是通过一个线性网络self.project_node_embeddings = nn.Linear(embedding_dim, 3 * embedding_dim, bias=False) 实现的。
经过一次8头注意力网络后得到新的上下文结点$h_c^{(N+1)}$，经过线性变换后得到单头注意力层的query，经过单头注意力机制后得到相关性分数logits：
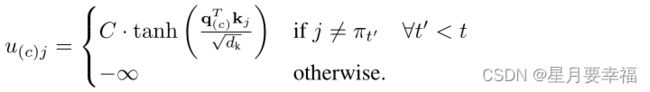这里的注意力层没有采用跳跃连接、批归一化、全连接层操作，直接得到相关性分数。
def _one_to_many_logits得到每一次经过两层注意力层后的相关性分数

def _one_to_many_logits(self, query, glimpse_K, glimpse_V, logit_K, mask):

  batch_size, num_steps, embed_dim = query.size()
  key_size = val_size = embed_dim // self.n_heads

  # Compute the glimpse, rearrange dimensions so the dimensions are (n_heads, batch_size, num_steps, 1, key_size)
  glimpse_Q = query.view(batch_size, num_steps, self.n_heads, 1, key_size).permute(2, 0, 1, 3, 4)

  # Batch matrix multiplication to compute compatibilities (n_heads, batch_size, num_steps, graph_size)
  compatibility = torch.matmul(glimpse_Q, glimpse_K.transpose(-2, -1)) / math.sqrt(glimpse_Q.size(-1))
  if self.mask_inner:
      assert self.mask_logits, "Cannot mask inner without masking logits"
      compatibility[mask[None, :, :, None, :].expand_as(compatibility)] = -math.inf

  # Batch matrix multiplication to compute heads (n_heads, batch_size, num_steps, val_size)
  heads = torch.matmul(torch.softmax(compatibility, dim=-1), glimpse_V)

  # Project to get glimpse/updated context node embedding (batch_size, num_steps, embedding_dim)
  glimpse = self.project_out(
      heads.permute(1, 2, 3, 0, 4).contiguous().view(-1, num_steps, 1, self.n_heads * val_size))

  # Now projecting the glimpse is not needed since this can be absorbed into project_out
  # final_Q = self.project_glimpse(glimpse)
  final_Q = glimpse
  # Batch matrix multiplication to compute logits (batch_size, num_steps, graph_size)
  # logits = 'compatibility'
  logits = torch.matmul(final_Q, logit_K.transpose(-2, -1)).squeeze(-2) / math.sqrt(final_Q.size(-1))

  # From the logits compute the probabilities by clipping, masking and softmax
  if self.tanh_clipping > 0:
      logits = torch.tanh(logits) * self.tanh_clipping
  if self.mask_logits:
      logits[mask] = -math.inf

  return logits, glimpse.squeeze(-2)

通过采样/贪心策略选择结点，得到序列
def _inner输出每一步概率与最终结点序列

def _inner(self, input, embeddings):

  outputs = []
  sequences = []

  state = self.problem.make_state(input)

  # Compute keys, values for the glimpse and keys for the logits once as they can be reused in every step
  fixed = self._precompute(embeddings)

  batch_size = state.ids.size(0)

  # Perform decoding steps
  i = 0
  while not (self.shrink_size is None and state.all_finished()):

      if self.shrink_size is not None:
          unfinished = torch.nonzero(state.get_finished() == 0)
          if len(unfinished) == 0:
              break
          unfinished = unfinished[:, 0]
          # Check if we can shrink by at least shrink_size and if this leaves at least 16
          # (otherwise batch norm will not work well and it is inefficient anyway)
          if 16 <= len(unfinished) <= state.ids.size(0) - self.shrink_size:
              # Filter states
              state = state[unfinished]
              fixed = fixed[unfinished]

      log_p, mask = self._get_log_p(fixed, state)

      # Select the indices of the next nodes in the sequences, result (batch_size) long
      selected = self._select_node(log_p.exp()[:, 0, :], mask[:, 0, :])  # Squeeze out steps dimension
      
      state = state.update(selected)

      # Now make log_p, selected desired output size by 'unshrinking'
      if self.shrink_size is not None and state.ids.size(0) < batch_size:
          log_p_, selected_ = log_p, selected
          log_p = log_p_.new_zeros(batch_size, *log_p_.size()[1:])
          selected = selected_.new_zeros(batch_size)

          log_p[state.ids[:, 0]] = log_p_
          selected[state.ids[:, 0]] = selected_

      # Collect output of step
      outputs.append(log_p[:, 0, :])
      sequences.append(selected)

      i += 1

  # Collected lists, return Tensor
  return torch.stack(outputs, 1), torch.stack(sequences, 1)  # (512,20,20)  (512,20)

训练

1. 定义model
2. 初始化baseline：baseline = RolloutBaseline(model, problem, opts) 构建了数据集（10000，20，2），batch_size=1024，设置搜索方式为贪心，初始化baseline参数
3. 训练：
   for epoch in range(n_epochs–100):
   train_epoch:
   ----构建数据集（1280000，20，2），batch_size=512；设置搜索方式为采样：
   ----for batch in training_dataloader：
   ----train_batch：
   --------分别计算baseline和model通过attention后的cost（512，1）
   --------计算平均损失
   ​--------optimizer优化
   ​----对比二者的cost，通过baseline.epoch_callback()判断是否更新参数

• 代码中初始化baseline和训练过程中数据集的大小是不一样的
• 每经过一个epoch，才判断baseline是否更新（不是batch_size)

实验

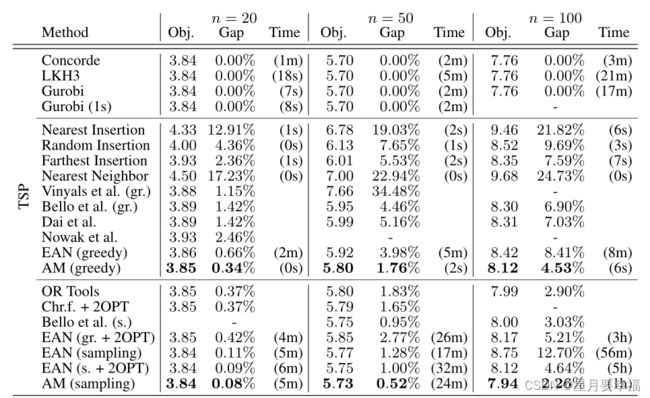
AM模型相比于其它深度学习模型，准确率更佳。
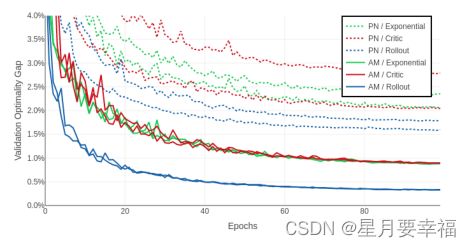
对比注意力网络和指针网络，注意力网络表现更好；相同网络中Rollout基线表现更好。

特别感谢：https://zhuanlan.zhihu.com/p/375218972
完整代码：https://github.com/wouterkool/attention-learn-to-route