论文精读:《FCOS3D: Fully Convolutional One-Stage Monocular 3D Object Detection》
文章目录
- 论文精读
-
- 摘要(Abstract)
- 1. 介绍(Introduction)
- 2. 相关工作(Related Work)
- 3. 方法(Approach)
-
- 3.1 框架总览(Framework Overview)
- 3.2 2D引导的多层次3D预测(2D Guided Multi-Level 3D Prediction)
- 3.3 二维高斯分布的三维中心度(3D Center-ness with 2D Gaussian Distribution)
论文精读
摘要(Abstract)
单目三维目标检测具有成本低的优点,是自动驾驶的一项重要任务。 由于其固有的不适定特性,其主要表现为缺乏深度信息,因而比传统的二维情形更具挑
战性。 二维检测的最新进展为更好地解决这一问题提供了机会。 然而,使一个通用的自适应二维探测器在这种三维任务中工作是不简单的。 本文以一个全卷积的单级检测器为例,对该问题进行了研究,并提出了一个通用框FCOS3D。 具体来说,我们首先将统一定义的7自由度三维目标变换到图像域,将它们解耦为二维和三维属性。 然后,根据目标的二维尺度将其分配到不同的特征层,并仅根据训练过程中指定的三维中心进行分配。 再者, 在三维中心的基础上,用二维高斯分布重新定义中心度,以拟合三维目标公式。所有这些使得该框架简单而有效,摆脱了任何2D检测或2D-3D关联先验。 在NeurIPS 2020的Nuscenes 3D检测中,我们的解决方案在所有的纯视觉方法中排名第一。
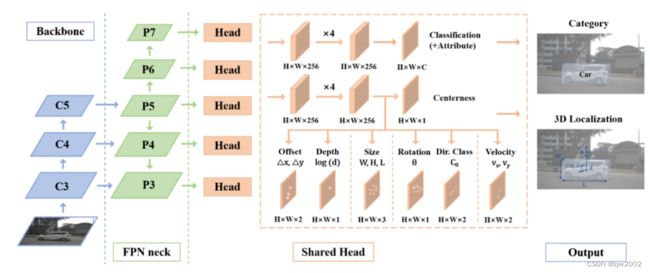
图1: 2D检测和单目3D对象检测的说明。 给定输入的RGB图像,二维无锚检测器需要预测从前景点到四个方框边的距离。 相比之下,单目3D无锚检测器需要预测转换后的3D中心、3D大小和物体的方向。
1. 介绍(Introduction)
目标检测是计算机视觉中的一个基本问题。 它的目的是识别图像中感兴趣的对象,并用相应的二维约束检测盒预测它们的类别。 随着深度学习的快速进展,二维物体检测近年来得到了很好的探索。 Faster R-CNN[27]、RetinaNet[18]、FCOS[31]等各种模型显著推动了该领域的进步,并有益于自动驾驶等各种应用。 然而,对于一个智能代理来说,二维信息不足以感知三维现实世界。 例如,当自动驾驶车辆需要在道路上平稳、安全地行驶时,它必须拥有周围物体的精确三维信息,才能做出安全决策。 因此,三维目标检测在这些机器人应用中变得越来越重要。 大多数最先进的方法[39、14、29、32、41、42]依赖于激光雷达点云提供的精确3D信息,但在每辆车上安装昂贵的激光雷达是一个沉重的负担。 因此,单目三维目标检测作为一种简单、廉价的部署环境,成为当今一个非常有意义的研究课题。
考虑到单目二维和三维目标检测具有相同的输入而不同的输出,单目三维目标检测的一个简单解决方案是遵循二维领域的做法,增加额外的分量来预测目标的额外三维属性。 以前的一些工作[30,20]继续预测2D盒子,并进一步在2D中心和感兴趣的区域上回归3D属性。 其他[1,9,2]用对应于每个2D锚点的3D先验值同时预测2D和3D盒。 另一种基于冗余3D信息[13,16]的方法流预测最终优化结果的额外关键点。 总之,如何将三维目标分配到具有二维对应关系的二维域中,并对其进行预测是一个基本的问题。
在本文中,我们采用了一种简单而有效的方法,使二维检测器能够预测三维定位。 我们首先将一般定义的7自由度三维位置投影到二维图像上,得到投影的中心点,相对于以前的二维中心,我们将其命名为三维中心。 通过这种投影,三维中心包含2.5D信息,即2D位置及其对应的深度。 2D位置可以进一步简化为图像上某一点的2D偏移量,该偏移量作为唯一可以在不同特征级别之间归一化的2D属性,就像在2D检测中一样。 相比之下,深度、3D大小和方向被视为解耦后的3D属性。 这样,我们用基于中心的范式对三维目标进行变换,避免了任何必要的2D检测或2D-3D对应先验。
作为一个实际的实现,我们将我们的方法建立在FCOS[31]上,这是一个简单的无锚的全卷积单级检测器。 首先根据目标的二维尺度将其分布到不同的特征层。 然后仅根据投影的三维中心来分配每个训练样本的回归目标。 与用距离表示中心度的FCOS不同,我们用基于三维中心的二维高斯分布来表示三维中心度。 我们在一个流行的大规模数据集Nuscenes[3]上评估了我们的方法,并在没有任何先验信息的情况下在该基准的相机跟踪中获得了第一名。 而且,我们只需要少2倍的计算资源,就可以在一天内训练一个性能与以前最好的开源方法CenterNet[38]相当的基线模型,也比它快3倍。 两者都表明我们的框架是简单和高效的。 详细的消融研究显示了每个组成部分的重要性。
2. 相关工作(Related Work)
- 2D目标检测
二维目标检测随着深度学习方法的突破,二维目标检测的研究取得了长足的进展。 根据初始猜测的基础,现代方法可分为基于锚点和无锚点两大分支。 基于锚点的方法[10,27,19,26]受益于预定义的锚点,因为回归更加容易,同时有许多超参数要调优。 相比之下,无锚点方法[12,25,31,15,38]不需要这些先前的设置,因此更加整洁,具有更好的通用性。 为了简单起见,考虑到FCOS对重叠地面实况的处理能力和尺度方差问题,本文采用了具有代表性的无锚检测器FCOS作为基线。 从另一个角度看,单目三维检测是与二维检测密切相关的一项难度更大的任务。 但对二者的联系和区别却鲜有研究,这使得二者相互孤立,无法从彼此的进步中获益。 本文旨在以FCOS为例,进一步在这两个任务之间建立更紧密的联系。
- 单目3维目标检测
单目三维目标检测单目三维目标检测比传统的二维目标检测复杂。 潜在的关键问题是输入的二维数据模型和输出的三维预测不一致。
涉及子网络的方法 (Methods involving sub-networks)
第一批作品借助子网络辅助三维检测。 仅举几个例子,3DOP[4]和MLFusion[36]使用深度估计网络,而Deep3Dbox[21]使用2D物体探测器。 它们严重依赖子网络的性能,甚至依赖外部数据和预先训练的模型,使得整个系统复杂且不便于训练。
转换成3D表示 (Transform to 3D representations)
另一类方法将输入的RGB图像转换为其他3D表示,如体素[28]和点云[35]。 最近的工作[37,23,34,24]遵循这一方法取得了很大进展,并显示出有希望的性能。 然而,它们仍然依赖于密集的深度标签,因此不被视为纯粹的单目方法。 不同深度传感器和激光雷达之间也存在领域差距,这使得它们很难顺利地推广到新的实践环境中。 另外,将这些方法应用到现实场景中,很难处理大量的点云。
端到端的设计(End-to-end design like 2D detection)
端到端的设计,如2D检测,最近的工作注意到这些缺点,并开始设计端到端的框架,如2D检测器。 例如,M3D-RPN[1]提出了一种具有端到端区域建议网络和深度感知卷积的单级检测器。 SS3D[13]检测二维关键点,并进一步预测具有不确定性的物体特征。 Monodis[30]改进了多任务学习与解纠缠损失。 这些方法遵循基于锚点的方式,因此需要定义一致的2D和3D锚点。 其中一些还需要多个培训阶段或手工制作的优化后阶段。 相比之下,无锚方法[38,16,5]不需要对给定的数据进行统计。 将它们的简单设计推广到具有更多不同类或不同内在设置的更复杂的情况更方便。 因此,我们选择遵循这一范式。
然而,这些工作很少研究将一般的二维检测器应用于单目三维检测的关键难点。 在提出它们的新框架时,很少讨论其中应保留或调整的内容。 相比之下,本文对这一点进行了研究,为将一个典型的二维检测器框架应用于密切相关的任务提供了参考。 在此基础上,更深入地了解这两项任务之间的联系和区别,也将有利于双方社区的进一步研究。
3. 方法(Approach)
目标检测是场景理解中最基本、最具挑战性的问题之一。 传统的二维目标检测的目标是预测每个感兴趣对象的二维包围盒和类别标签。 相比之下,单目三维检测需要我们预测三维包围盒,而这些包围盒需要解耦并转换到二维图像平面。 本节将首先概述我们采用的三维目标重构框架,然后详细阐述两种相应的技术设计,即二维引导的多级三维预测(2D guided multi-level 3D prediction)和二维高斯分布的三维中心度(3D center-ness with 2D Gaussian distribution)。 这些技术设计共同作用使二维探测器FCOS具有探测三维物体的能力。
3.1 框架总览(Framework Overview)
全卷积单级检测器通常由三个部分组成:用于特征提取的主干、用于多级分支构造的颈和用于密集预测的检测头。 然后我们简单地介绍了每一个。
图2:我们的检测流程的概述。 为了充分利用发展良好的二维特征提取器,我们基本上遵循典型的二维检测器骨干和颈部的设计。 对于检测头,我们首先用基于中心的范式对三维目标进行重构,将其解耦为多任务学习。 对多级目标分配和中心采样策略进行了相应的调整,使该框架具有更好的处理重叠真实框和尺度方差问题的能力。
Backbone
我们使用预训练的Resnet101[11,8]和deformable convolutions[7]进行特征提取。 在我们的实验中,它在精度和效率之间取得了很好的折衷。 我们固定了第一个卷积块的参数,以避免更多的内存开销。
Neck
第二个模块是特征金字塔网络[17],它是在不同尺度上检测物体的主要部件。 为了精确的澄清,我们将3到7级的特征图表示为P3到P7,如图所示 2. 我们遵循原始FCOS得到P3到P5,并用两个卷积块对P5下采样得到P6和P7。 所有这五个特征图都负责不同尺度的预测。
Detection Head
最后,对于共享检测头,我们需要处理两个关键问题。 首先是如何将目标分配到不同的特征层和不同的点。 它是不同探测器的核心问题之一。 二是如何进行架构设计。 我们遵循RetinaNet[18]和FCOS[31]的常规设计。 每个共享头由4个共享卷积块和针对不同目标的小头组成。 在经验上,用不同的测量为回归目标建立额外的分离头更有效,所以我们为每个目标设置一个小头(图2)。 到目前为止,我们已经介绍了我们网络架构的总体设计。 接下来,我们将更正式地阐述这个问题,并给出详细的训练和推理程序。
Regression Targets
首先,我们回顾了FCOS中用于目标检测的无锚点方式。 在主干的第 i i i层给出一个特征映射,表示为 F i ∈ R H × W × C F_i \in \mathbb{R}^{H \times W \times C} Fi∈RH×W×C,我们需要根据该特征映射上的每个点来预测目标,这些点对应于原始输入图像上均匀分布的点。 形式上,对于特征图 F i F_i Fi上的每个位置 ( x , y ) (x,y) (x,y),假设直到图层I的总步幅为 s s s,则原始图像上对应的位置应为 ( s x + ⌊ s 2 ⌋ , s y + ⌊ s 2 ⌋ ) \left(s x+\left\lfloor\frac{s}{2}\right\rfloor, s y+\left\lfloor\frac{s}{2}\right\rfloor\right) (sx+⌊2s⌋,sy+⌊2s⌋)。与基于锚点的检测器通过预先定义的锚点作为参考来回归目标不同,我们直接根据这些位置来预测目标。 而且,由于我们不依赖主播,判断一个点是否来自前景的标准将不再是主播与地面真理之间的IOU(交集对并)。 相反,只要点足够靠近盒子中心,它就可以是前景点。
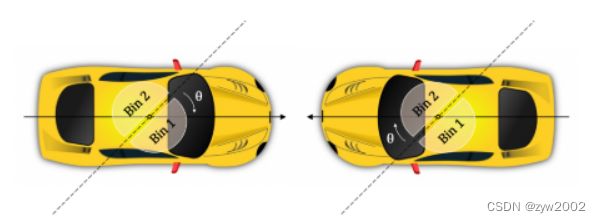
在二维情况下,模型需要将点的距离回归到顶/底/左/右,在图中表示为 t , b , l , r t,b,l,r t,b,l,r 然而,在3D情况下,将距离回归到3D包围盒的六个面是不平凡的。 相反,一个更直接的实现是将通常定义的7自由度回归目标转换为2.5D中心和3D大小。 2.5D的中心可以很容易地转换回三维空间与相机的内在矩阵。 对2.5D中心的回归可以进一步简化为分别回归从中心到特定前景点的偏移量,Δx,Δy及其对应的深度d。 另外,为了预测物体的异心方位,我们将其分为角度θ随周期π和2-bin方向分类两部分。 第一个组件自然地用基本的真实框来模拟我们预测的IOU,而第二个组件侧重于两个盒子具有相反方向的对抗性情况。 利用这种角度编码,我们的方法在定位精度方面超过了另一种基于中心的框架CenterNet,并将在实验中进行比较。 在图3中说明了旋转编码方案。
除了这些与目标位置和方向相关的回归目标外,我们还回归了一个类似FCOS的二元目标中心度(center-ness) c c c。 它作为一个软二值分类器来确定哪些点更接近中心,并帮助抑制那些远离目标中心的低质量预测。
综上所述,回归分支需要预测的对象是 x 、 y 、 d 、 w 、 l 、 h 、 θ 、 v x 、 v y x、y、d、w、l、h、θ、v_x、v_y x、y、d、w、l、h、θ、vx、vy
、方向类 C θ C_θ Cθ和中心度 c c c,分类分支则需要输出对象的类标签和属性标签(图2)。
Loss
对于分类和
不同的回归目标,我们分别定义了它们的损失,并以它们的加权总和作为总损失。 首先,对于分类分支,我们使用了常用的焦点损失[18],用于对象分类损失:
L c l s = − α ( 1 − p ) γ log p L_{c l s}=-\alpha(1-p)^\gamma \log p Lcls=−α(1−p)γlogp
其中 p p p是预测框的类概率。 我们遵循原论文的设置, α = 0.25 \alpha=0.25 α=0.25 和 γ = 2 \gamma=2 γ=2。 对于属性分类,我们使用一个简单的Softmax分类损失,表示为 L a t t r L_{a t t r} Lattr
对于回归分支,我们对除中心度外的每个回归目标使用光滑的 L 1 L_1 L1损失,并考虑其尺度,给出相应的权重:
L l o c = ∑ b ∈ ( Δ x , Δ y , d , w , l , h , θ , v x , v y ) SmoothL1 ( Δ b ) L_{l o c}=\sum_{b \in\left(\Delta x, \Delta y, d, w, l, h, \theta, v_x, v_y\right)} \operatorname{SmoothL1}(\Delta b) Lloc=b∈(Δx,Δy,d,w,l,h,θ,vx,vy)∑SmoothL1(Δb)
其中, Δ x , Δ y , w , l , h , θ \Delta x, \Delta y, w, l, h, \theta Δx,Δy,w,l,h,θ 误差的权重为1, d d d 的权重为0.2, v x , v y v_x, v_y vx,vy 的权重为0.05。 注意,虽然我们使用exp(x)进行深度预测,但我们仍然在原始深度空间而不是日志空间中计算损失。 它的经验结果,更准确的深度估计最终。 我们使用Softmax分类损失和二元交叉熵(BCE)损失进行方向分类和中心度回归,分别表示为 L d i r L_{d i r} Ldir 和。 最后,总损失为:
L = 1 N p o s ( β c l s L c l s + β a t t r L a t t r + β l o c L l o c + β d i r L d i r + β c t L c t ) L=\frac{1}{N_{p o s}}\left(\beta_{c l s} L_{c l s}+\beta_{a t t r} L_{a t t r}+\beta_{l o c} L_{l o c}+\beta_{d i r} L_{d i r}+\beta_{c t} L_{c t}\right) L=Npos1(βclsLcls+βattrLattr+βlocLloc+βdirLdir+βctLct)
其中 N pos N_{\text {pos }} Npos 是预测的正样本, β c l s = β a t t r = β l o c = β d i r = β c t = 1 \beta_{c l s}=\beta_{a t t r}=\beta_{l o c}=\beta_{d i r}=\beta_{c t}=1 βcls=βattr=βloc=βdir=βct=1.
Inference
在推理过程中,给定一个输入图像,我们通过框架转发它,并获得包含它们的类分数、属性分数和中心预测的包围盒。 我们将类得分和中心度相乘作为每个预测的置信度,并在鸟视图中进行旋转非最大抑制(NMS)作为大多数三维检测器来得到最终结果。
图3:我们利用的旋转编码方案。 基于2-bin边界,两个方向相反的物体共享相同的旋转偏移量,从而具有相同的sin值。 为了区分它们,我们从回归分支中预测一个额外的方向类。
3.2 2D引导的多层次3D预测(2D Guided Multi-Level 3D Prediction)
如前所述,要用金字塔网络训练一个检测器,我们需要设计一个策略来将目标分配到不同的特征级别。 FCOS[31]在其中讨论了两个关键问题:1)如何使无锚点检测器实现与基于锚点的检测器相似的最佳可能召回(BPR);2)由地面真值盒重叠引起的难以解决的模糊性问题。 原论文中的比较很好地解决了第一个问题。 结果表明,通过FPN进行多级预测可以改善业务流程再造,甚至比基于锚点的方法取得更好的效果。 同样,这个问题的结论在我们的改编框架中也是适用的。 第二个问题将涉及回归目标的具体设置,我们接下来将讨论这个问题。
原始的FCOS在不同级别的特征映射中检测不同大小的物体。 与基于锚点的方法不同的是,它不是指定不同大小的锚点,而是直接将不同大小的地面真相盒分配到不同层次的特征图中。 形式上,首先计算每个位置在每个特征层的二维回归目标 l ∗ , r ∗ , t ∗ , b ∗ l^*, r^*, t^*, b^* l∗,r∗,t∗,b∗. 位置满足 max ( l ∗ , r ∗ , t ∗ , b ∗ ) > m i \max \left(l^*, r^*, t^*, b^*\right)>m_i max(l∗,r∗,t∗,b∗)>mi 和 max ( l ∗ , r ∗ , t ∗ , b ∗ ) < m i − 1 \max \left(l^*, r^*, t^*, b^*\right)
接下来,我们将讨论如何处理歧义问题。 具体地说,当一个点在同一特征级别的多个地面真值盒内时,应该给它分配哪个盒子? 通常的方式是根据二维包围盒的面积进行选择。 选择面积较小的框作为此点的目标框。 我们称此方案为基于区域的准则。 该方案有一个明显的缺点:大对象将被这样的处理所关注的较少,这也被我们的实验(图4)所验证。 考虑到这一点,我们提出了一个基于距离的准则,即选择中心较近的方框作为回归目标。 该方案与自适应的基于中心的回归目标定义机制是一致的。 此外,由于离目标中心较近的点可以获得更全面、更均衡的局部区域特征,从而容易产生更高质量的预测结果,因此这种方法也是合理的。 通过简单的验证(图4),我们发现该方案显著提高了大型物体的最佳可能召回率(BPR)和MAP,并提高了整体MAP(约1%),这将在消融研究中呈现。
除了基于中心的模糊处理方法外,我们还使用三维中心来确定前景点,即只有足够靠近中心的点才被视为正样本。 我们定义了一个超参数,半径,来测量这个中心部分。 在我们的实验中,半径为1.5时,距离小于半径×步幅的点被认为是正的。
最后,我们将不同回归分支的每个输出 x x x替换为6个,以区分不同特征级别的共享头。 这里 s i s_i si是一个可训练标量,用于调整特征级别 i i i的指数函数基。 它在检测性能方面带来了微小的改进。
3.3 二维高斯分布的三维中心度(3D Center-ness with 2D Gaussian Distribution)
在FCOS的原始设计中,中心度C是由二维回归目标 l ∗ , r ∗ , t ∗ , b ∗ : l^*,r^*,t^*,b^*: l∗,r∗,t∗,b∗:
c = min ( l ∗ , r ∗ ) max ( l ∗ , r ∗ ) × min ( t ∗ , b ∗ ) max ( t ∗ , b ∗ ) c=\sqrt{\frac{\min \left(l^*, r^*\right)}{\max \left(l^*, r^*\right)} \times \frac{\min \left(t^*, b^*\right)}{\max \left(t^*, b^*\right)}} c=max(l∗,r∗)min(l∗,r∗)×max(t∗,b∗)min(t∗,b∗)
由于回归目标改为基于三维中心的范式,我们以投影的三维中心为原点,用二维高斯分布定义中心度。 二维高斯分布简化为:
c = e − α ( ( Δ x ) 2 + ( Δ y ) 2 ) c=e^{-\alpha\left((\Delta x)^2+(\Delta y)^2\right)} c=e−α((Δx)2+(Δy)2)
这里用 α α α来调节从中心到外围的光强衰减,在我们的实验中设置为2.5。 我们将其作为中心性的基本真理,并从回归分支中对其进行预测,以过滤低质量的预测。 如前所述,该中心度目标的范围为0到1,因此我们使用二进制交叉熵(BCE)损失来训练该分支。