递归算法应用

一、计算数的阶乘函数

二、计算数的非负整数次幂

三 、插入排序的递归算法

问题：对具有n个元素的数组进行非递减排序

输入：数组A[]，数组中的元素个数为n

输出：按非递减顺序排列的数组A[]

思路：当数组元素个数多余一个时，递归排好前n-1个元素的顺序，然后循环找到第n个元素合适的位置

四、多项式求值的递算法

问题：计算n阶多项式的值：=++......++

输入：存放于数组的多项式系数A[]及x，多项式的阶数n

输出：阶数为n的多项式的值

思路：使用秦九韶算法将公式改写：

=++......++

=((...(((()x+)x+)+)+...)x+)x+

1.当n=0时，=(A[0])

2.=

   =

   .....

3.对于任意的k（k=1,2,3,...,n）,前面的k-1步已经计算出,即

        

         所以：(A[k])

         即(A[n])

注意：多项式系数的在数组中是这样存放的，存放在A[0]中，存放在A[1]中，以此类推。。

 五、排列问题的递归算法

问题：将具有n个元素的数组A进行排列，找到所有排列顺序，对它们的编号为1,2，..，n

输入：数组A[]，数组的元素个数为n，当前递归层次需要完成排列的元素个数为k

输出：数组A[]的全部排列情况

思想步骤:

一、

1.数组的第一个元素为1，生成后面的n-1个元素的排列

2.将第一个元素与第二个元素交换，使第一个元素为2，然后生成后面n-1个元素的排列

。。。。

将第一个元素与第n个元素交换，使第一个元素为n，然后生成后面n-1个元素的排列

二、在上面步骤中，为了生成后面n-1个元素的排列，继续采取以下步骤

1.数组的第二个元素为2，生成后面的n-2个元素的排列

2.将第二个元素与第三个元素交换，是第二个元素为3，然后生成后面n-2个元素的排列

。。。

将第二个元素与第n个元素交换，使第二个元素为n，然后生成后面n-2个元素的排列

三、为了完成生成后面n-2个元素的排列，需要交换第三个元素

。。。。

N-1、数组的第n-1个元素为n-1,将数组的第n-1个元素与第n个元素交换，使数组的第n-1个元素为n，生成后面1个元素的排列，此时数组已经完成了一个排列

如果排列算法pl_alm(A,k,n)表示生成数组后面的k个元素的排列，通过上面的分析，得出以下结论：

1.当k=1时，只有一个元素，已经形成了一个排序

2.对于任意的k(k=2,3,...)，可以根据算法pl_alm(A,k-1,n)完成数组后面k-1个元素的排序，那么要完成pl_alm(A,k,n)数组后面k个元素的排序，需要将数组中的第n-k个元素逐一与数组中n-k~n元素进行交换，每次交换都要进行一次pl_alm(A,k-1,n)，然后还要将交换的元素交换回来，保证每次交换时第k个元素为k

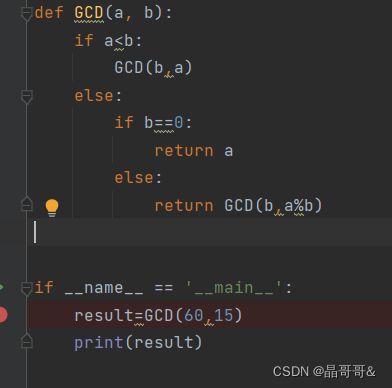
 六、最大公约数的递归算法

问题：求两个数的最大公约数

辗转相除法原理（学习CSDN博主：哈哈哈哈嘻哈从）：

1、辗转相除法与更相减损术在求最大公约数有相同的核心原理：

举例解释更相减损术，例如求161与63的最大公约数，设最大公约数为m

161=63+98,63与98的和161的最大公约数是m，63的最大公约数也是m，所以98也可被m整除

所以就转换成98与63的最大公约数

98=63+35,63与35的和98的最大公约数是m，63的最大公约数也是m，所以35也可被m整除

所以就转换成35与63的最大公约数

同理63=35+28，所以就转换成28与35的最大公约数

然后是7与28的最大公约数

然后是7与21的最大公约数

。。。

然后是7与7的最大公约数

然后是7与0的最大公约数

由此可以看出最大公约数为7

2、辗转相除法原理：小将较大数除以较小数，得到的余数，在余数（第一次余数）和前面的除数中进行比较大小，然后继续用大的除以小的得到新的余数，然后在将得到的新的余数（第二次余数）与前面的除数比较大小，继续进行相除得余数，反复如此，直至进行比较的两个数中有一个为0，结束算法，另一个数即为最大公约数

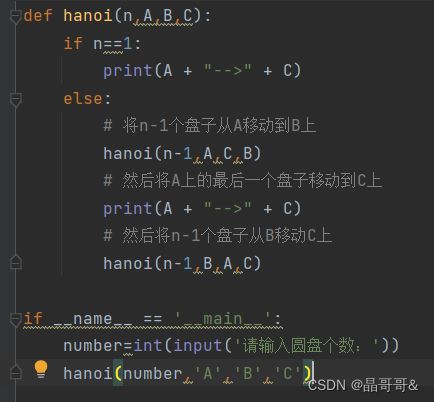
 七、汉诺塔问题

问题：圆盘的个数为n，圆盘最开始在A柱子上，然后将这n个圆盘移动到C柱子上，B柱子为过渡柱子，其中每次只能移动一个圆盘，且大盘子不能压在小盘子上

思路：（全局观看问题）

将A柱子上的n-1个盘子利用递归算法移动到B柱子上，然后将A柱子上的一个圆盘移动到C柱子上，然后将B柱子上的n-1个圆盘利用递归算法移动到C柱子上。

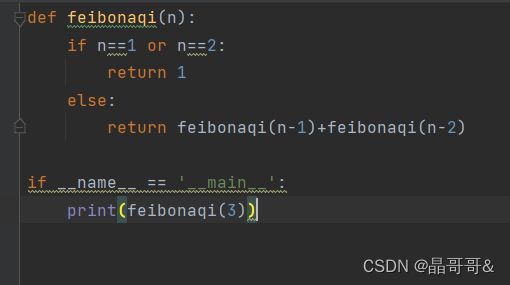
 八、斐波那契数递归算法

问题：求斐波那契数的第n（n>=1）个数是多少

思路：斐波那契数的规律是当前数等于该数的前两个数的和