CNN 图像分类

CNN实现对FashionMNIST图像分类

卷积神经网络相对于全连接神经网络的优势：

1. 参数少 -> 权值共享
   因为全连接神经网络输入的图片像素较大， 所以参数较多
   而卷积神经网络的参数主要在于核上， 而且核的参数可以共享给其他通道
2. 全连接神经网络会将输入的图片拉直， 这样就会使图片损失原来的效果，从而导致效果不佳
   而卷积神经网络不会将图片拉直，用步长去移动核
3. 可以手动选取特征，训练好权重，特征分类效果比全连接神经网络的效果好

CNN过程：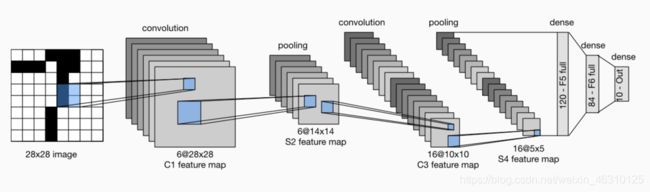

conolution层： 实现对feature map局部采样(相似于感受野)
pooling层: 增加感受野
dense层: 也就是全连接层

大概思路

1. 加载数据集
2. 构建CNN模型
3. 训练函数
4. 训练模型
5. 可视化效果

使用pytorch实现CNN

使用的是Fashimnist数据集， 和以前的线性回归加载数据集的方式一样

日常导入需要用到的python库

import torch
import torch.nn as nn
import torch.optim as optim
import torch.functional as F
import torchvision
import torchvision.transforms as transforms
import numpy as np

import matplotlib.pyplot as plt

加载数据集

与线性回归一样， 就不再阐述

# 加载数据集
train_data = torchvision.datasets.FashionMNIST("/home/kesci/input/FashionMNIST2065",
                train=True,
                transform=transforms.ToTensor(),
                download=False)
                
test_data = torchvision.datasets.FashionMNIST("/home/kesci/input/FashionMNIST2065",
                train=False,
                transform=transforms.ToTensor(),
                download=False)

# 批量加载数据
train_iter = torch.utils.data.DataLoader(train_data, batch_size=64,
                shuffle=True,
                num_workers=4)
test_iter = torch.utils.data.DataLoader(train_data, batch_size=64,
                shuffle=False,
                num_workers=4)

构建模型

与上面的图片相似

简述一下第一层卷积层， 第二次卷积层原理一样

输入通道为1（ 因为我们输入的图片是灰度图）
输出通道为6
使用5 * 5 的核
并在图片边缘各加两行两列的全0填充
使用默认的步长1

卷积的计算公式

Input(N_batch, C_inchannel, H_inheight, W_inweight)
Output(N_batch, C_inchannel, H_outheight, W_outweight)
H_outheight = (H_inheight + 2 * padding - (kernel_h - 1) - 1) / s + 1
W_outweight = (W_outweight + 2 * padding - (kernel_w - 1) - 1) / s + 1

第一层卷积：
输入（batch_size， 1， 28， 28）
h_out = (28 + 2 * 2 - (5 - 1) - 1) / 1 + 1 = 28
w_out = (28 + 2 * 2 - (5 - 1) - 1) / 1 + 1 = 28
输出（batch_size， 6， 28， 28)
第一层池化层：
输入（batch_size， 6， 28， 28）
输出（batch_size， 6， 14， 14）
第二层卷积：
输入（batch_size， 6， 14， 14）
输出（batch_size， 16， 10， 10）
第二层池化层：
输入（batch_size， 16， 10， 10）
输出（batch_size， 16， 5， 5）
全连接层：
（batch_size， 16 * 5 * 5） -> （batch_size， 120）-> （batch_size， 84）-> （batch_size， 10）

# 构建模型
from collections import OrderedDict
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Sequential(OrderedDict([
                # (28 + 2 * 2 - (5 - 1) - 1) / 1 + 1 = 28
                ("conv", nn.Conv2d(1, 6, 5, padding=2)),
                ("relu", nn.ReLU()),
                ("pool", nn.MaxPool2d(2, 2)),
            ]))
            
        self.conv2 = nn.Sequential(OrderedDict([
                # (14 - (5 - 1) - 1) / 1 + 1 = 10
                ("conv", nn.Conv2d(6, 16, 5)),
                ("relu", nn.ReLU()),
                ("pool", nn.MaxPool2d(2, 2)),
            ]))
        
        self.fc = nn.Sequential(OrderedDict([
                ("flatten", nn.Flatten()),
                ("fc1", nn.Linear(400, 120)),
                ("dropout1", nn.Dropout(.4)),
                ("fc2", nn.Linear(120, 84)),
                ("dropout2", nn.Dropout(.4)),
                ("fc_out", nn.Linear(84, 10))
            ]))
        
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.fc(x)
    
        return x

训练函数

基本思路

def train(net, lr=.01, epochs=20):
    opt = optim.Adam(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    for epoch in range(1, epochs + 1):
        train_loss = 0
        test_loss = 0
        for x, y in train_iter:
            out = net(x)
            l = loss(out, y)
            
            net.zero_grad()
            l.backward()
            opt.step()
            
            train_loss += l.item()
        
        acc = 0.0
        if epoch % 4 == 0:
            for x, y in train_iter:
                out = net(x)
                l = loss(out, y)
                test_loss += l.item()
                
                acc += (out.argmax(1) == y).float().mean().item()
            
            print(f"Epoch: {epoch}: \n"
                    f"Train Loss: {train_loss / len(train_iter) :.3f}\t"
                    f"Test Loss: {test_loss / len(test_iter) :.3f}\t"
                    f"Accuracy: {acc / len(test_iter) :.3f}\n")
            

训练模型和可视化

model = Model()
train(model)

结果：
Epoch: 4:
Train Loss: 0.541 Test Loss: 0.538 Accuracy: 0.811

Epoch: 8:
Train Loss: 0.545 Test Loss: 0.512 Accuracy: 0.824

Epoch: 12:
Train Loss: 0.545 Test Loss: 0.548 Accuracy: 0.806

Epoch: 16:
Train Loss: 0.560 Test Loss: 0.549 Accuracy: 0.819

Epoch: 20:
Train Loss: 0.577 Test Loss: 0.568 Accuracy: 0.795

感觉是有点训练过头了

接着可视化

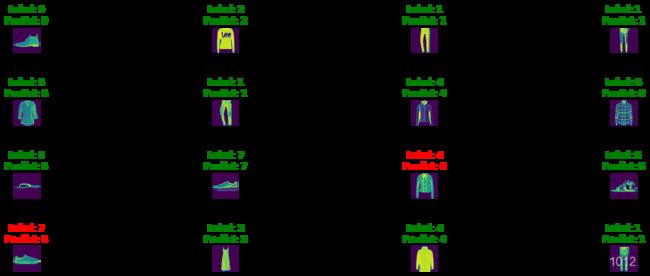
data = []
for i in range(16):
    data.append(test_data[i])
   plt.figure(figsize=(16, 6))
   
plt.subplots_adjust(wspace = 2, hspace=2)
for i in range(16):
    out = model(data[i][0].view(1, 1, 28, 28)).argmax(1).item()
    ax = plt.subplot(4, 4, i + 1)
    ax.imshow(data[i][0].view(28, 28).numpy())
    ax.set_title(f"Label: {data[i][1]}\nPredict: {out}", color="g" if out == data[i][1] else "r")
    ax.axis("off")
plt.show()

OK, 到这里也对CNN也有些了解了。
更多可以参考CNN的一些进阶模型， AlexNet、VGG、NiN、GoogLeNet等