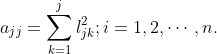数值分析·学习 | 平方根法和追赶法matlab实现

目录

一、前言：

二、算法描述：

三、实现代码：

1、平方根法：

2、改进的平方根法:

3、追赶法:

四、总结:

---

一、前言：

个人学习内容分享

---

二、算法描述：

平方根法：

        如果A为n阶对称正定矩阵，则存在一个实的非奇异下三角矩阵L,使,当限定L的对角元素为正时，这种分解是唯一的。

        下面我们用直接分解方法来确定计算L元素的递推公式，因为

                

        其中.由矩阵乘法及(当j

                

        于是得到对于求解Ax=b的平方根法计算公式：

        对于j=1,2,...,n

  

        求解Ax=b，即求解两个三角形方程组：

         ①Ly=b,求y;     ②LTx=y,求x.

        其中：

                        

所以

改进的平方根法：

        为了避免开方，我们下面用定理9的分解式A=

即 

        由矩阵乘法，并注意,得

        于是得到计算L得元及D得对角元素公式：

        对于i=1,2,...,n.

        为了避免重复计算，我们引进tij=lijdj,由上式得到按行计算L,T元素得公式：d1=a11

对于i=2,3,...,n.

        

        

        

        计算出T=LD的第i行元素tij(j=1,2,...,i-1)后，存放在A的第i行相应位置，然后再计算L的第i行元素，存放在A的第i行.D的对角线元素存放在A的相应位置。例如

        ​​​​​​​        

        对称正定矩阵A按分解和按分解计算量差不多，但分解不需要开方计算。 

        求解Ly=b,DLTx=y计算公式：

追赶法：

对于A为三对角矩阵时，可分解成以下形式

即可得到

        

从而求解Ax=f等价于解两个三角形方程组：

        ①Ly=f,求y,②Ux=y,求x.

进而追赶法公式为：

（1）计算{Bi}的递推公式

        

        

（2）解Ly=f

        

        

（3）解Ux=y

        

        

三、实现代码：

1、平方根法：

function X=squareRoot(A,b)
%%功能：平方根算法
n=length(A);
y=b;
X=y;
%变换矩阵
for k=1:n
    A(k,k)=sqrt(A(k,k));
    A(k+1:n,k)=A(k+1:n,k)/A(k,k);
    for j=k+1:n
        A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);
    end
end
%求解矩阵
for k=1:n
    y(k)=(b(k)- sum(A(k,1:k-1)*y(1:k-1)))/A(k,k);
end
A=A';
for k=n:-1:1
    X(k)=(y(k)-sum(A(k,k+1:n)*X(k+1:n)))/A(k,k);
end

---

2、改进的平方根法:

function X=ImprovedSquareRoot(A,b)
%%功能:改进的平方根公式
n=length(A);
v=b;
y=b;
X=b;
%变换矩阵
for j=1:n
    for k=1:j-1
        v(k)=A(j,k)*A(k,k);
    end
    A(j,j)=A(j,j)-sum(A(j,1:j-1)*v(1:j-1));
    for i=j+1:n
        A(i,j)=(A(i,j)-sum(A(i,k)*v(1:j-1)))/A(j,j);
    end
end
%求解矩阵
D=diag(diag(A));
A=A-D+diag(diag(ones(3)));
for k=1:n
    y(k)=(b(k)-sum(A(k,1:k-1)*y(1:k-1)))/A(k,k);
end
d=diag(D);
X(n)=y(n)/d(n);
for k=n-1:-1:1
    X(k)=y(k)/d(k)-sum(A(k+1:n,k).*X(k+1:n));
end
end

---

3、追赶法:

function X=CatchUpMethod(a,b,c,f)
%%功能：追赶法
n=length(b);
B=f;
B(1)=c(1)/b(1);
for k=2:n-1
    B(k)=c(k)/(b(k)-a(k)*B(k-1));
end
y(1)=f(1)/b(1);
for k=2:n
    y(k)=(f(k)-a(k-1)*y(k-1))/(b(k)-a(k-1)*B(k-1));
end
X(n)=y(n);
for k=n-1:-1:1
    X(k)=y(k)-B(k)*X(k+1);
end
end 

---

四、总结：