3. Python实现VRP常见求解算法——禁忌搜索（TS）

参考笔记
https://github.com/PariseC/Algorithms_for_solving_VRP

TS算法原理详解

禁忌搜索(Tabu Search)算法及python实现

• 邻域
  对于组合优化问题，给定任意可行解x，x∈D，D是决策变量的定义域，对于D上的一个映射：N：x∈D→N(x)∈2(D) 其中2(D)表示D的所有子集组成的集合，N(x)成为x的一个邻域，y∈N(x)称为x的一个邻居。
• 候选集合
  候选集合一般由邻域中的邻居组成，可以将某解的所有邻居作为候选集合，也可以通过最优提取，也可以随机提取，例如某一问题的初始解是[1,2,3]，若通过两两交换法则生成候选集合，则可以是[1,3,2],[2,1,3],[3,2,1]中的一个或几个。
• 禁忌表
  禁忌表包括禁忌对象和禁忌长度。由于在每次对当前解的搜索中，需要避免一些重复的步骤，因此将某些元素放入禁忌表中，这些元素在下次搜索时将不会被考虑，这些被禁止搜索的元素就是禁忌对象；
  禁忌长度则是禁忌表所能接受的最多禁忌对象的数量，若设置的太多则可能会造成耗时较长或者算法停止，若太少则会造成重复搜索。
• 评价函数
  用来评价当前解的好坏，TSP问题中是总旅程距离。
• 特赦规则
  禁忌搜索算法中，迭代的某一步会出现候选集的某一个元素被禁止搜索，但是若解禁该元素，则会使评价函数有所改善，因此我们需要设置一个特赦规则，当满足该条件时该元素从禁忌表中跳出。
• 终止规则
  一般当两次迭代得到的局部最优解不再变化，或者两次最优解的评价函数差别不大，或者迭代n次之后停止迭代，通常选择第三种方法。

举例详述TS算法过程

现有一架飞机，从A点出发，需要经过B,C,D,E,F之后返回A点，且每个点只能经过一次，最后返回A点，求最短路径。

该问题是一个Hamilton回路问题，其中起点和终点已经固定，因此我们可以将解形式记为，例如【A,D,C,F,E,A】,每次只需变换中间两个元素即可，现在我们将禁忌长度设置为2，候选集合长度定义为4，迭代次数为100，通过以下步骤能使读者更清洗的了解TS算法的步骤。

给定任意初始解 x1=【A,D,C,F,E,A】f(x1)=10，历史最优为10

我们发现对x1交换D和E时，f最优，此时x2=【A,E,C,F,D,A】 f(x2)=6，历史最优为6，将D-E放入禁忌表中

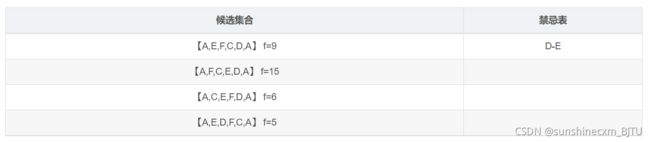
我们发现对x2交换C和D时，f最优，此时x3=【A,E,D,F,C,A】 f(x3)=5，历史最优为5，将D-C放入禁忌表中

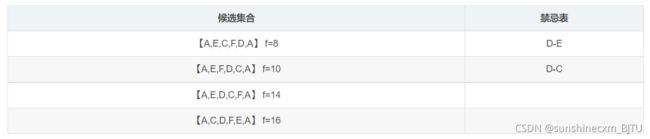
此时我们发现对x3交换D和C时最优，但是由于D-C已经在禁忌表中，因此我们退而求其次，对x3交换F和D，此时x4=【A,E,F,D,C,A】 f(x4)=10，历史最优为5， 将F-D放入禁忌表中，由于禁忌长度为2，因此将最先放入禁忌表中的D-E移除禁忌表

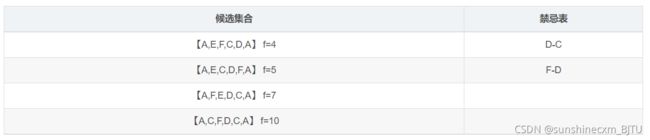
此时我们发现对x4交换D和C时最优，虽然D-C已经在禁忌表中，但是f(D-C)<历史最优5，因此满足特赦规则，现在将D-C移除禁忌表，此时x5=【A,E,F,C,D,A】 f(x5)=4，历史最优为4，然后再将D-C放入禁忌表

依次迭代下去，当迭代次数超过100时停止迭代，历史最优值即为输出解

1. 适用场景

• 求解CVRP
• 车辆类型单一
• 车辆容量不小于需求节点最大需求
• 单一车辆基地

2. 问题分析

CVRP问题的解为一组满足需求节点需求的多个车辆的路径集合。
假设某物理网络中共有10个顾客节点，编号为1~10，一个车辆基地，编号为0，在满足车辆容量约束与顾客节点需求约束的条件下，此问题的一个可行解可表示为：[0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0]，即需要4个车辆来提供服务，车辆的行驶路线分别为0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0。

由于车辆的容量固定，基地固定，因此可以将上述问题的解先表示为[1-2-3-4-5-6-7-8-9-10]的有序序列，然后根据车辆的容量约束，对序列进行切割得到若干车辆的行驶路线。 因此可以将CVRP问题转换为TSP问题进行求解，得到TSP问题的优化解后再考虑车辆容量约束进行路径切割，得到CVRP问题的解。这样的处理方式可能会影响CVRP问题解的质量，但简化了问题的求解难度。

3. 数据格式

以xlsx文件储存网络数据，其中第一行为标题栏，第二行存放车辆基地数据。在程序中车辆基地seq_no编号为-1，需求节点seq_id从0开始编号。可参考github主页相关文件。

4. 分步实现

（1）数据结构

为便于数据处理，定义Sol()类，Node()类，Model()类，其属性如下表：

• Sol()类，表示一个可行解

属性	描述
nodes_seq	需求节点seq_no有序排列集合，对应TSP的解
obj	优化目标值
action_id	解所对应的算子id，用于禁用算子
routes	车辆路径集合，对应CVRP的解

• Node()类，表示一个网络节点

属性	描述
id	物理节点id，可选
name	物理节点名称，可选
seq_no	物理节点映射id，基地节点为-1，需求节点从0编号
x_coord	物理节点x坐标
y_coord	物理节点y坐标
demand	物理节点需求

• Model()类，存储算法参数

属性	描述
best_sol	全局最优解，值类型为Sol()
node_list	物理节点集合，值类型为Node()
node_seq_no_list	物理节点映射id集合
depot	车辆基地，值类型为Node()
number_of_nodes	需求节点数量
tabu_list	禁忌表
TL	算子禁忌长度
opt_type	优化目标类型，0：最小车辆数，1：最小行驶距离
vehicle_cap	车辆容量

（2）文件读取

def readXlsxFile(filepath,model):
    # It is recommended that the vehicle depot data be placed in the first line of xlsx file
    node_seq_no = -1#the depot node seq_no is -1,and demand node seq_no is 0,1,2,...
    df = pd.read_excel(filepath)
    for i in range(df.shape[0]):
        node=Node()
        node.id=node_seq_no
        node.seq_no=node_seq_no
        node.x_coord= df['x_coord'][i]
        node.y_coord= df['y_coord'][i]
        node.demand=df['demand'][i]
        if df['demand'][i] == 0:
            model.depot=node
        else:
            model.node_list.append(node)
            model.node_seq_no_list.append(node_seq_no)
        try:
            node.name=df['name'][i]
        except:
            pass
        try:
            node.id=df['id'][i]
        except:
            pass
        node_seq_no=node_seq_no+1
    model.number_of_nodes=len(model.node_list)

（3）初始解生成

def genInitialSol(node_seq):
    node_seq=copy.deepcopy(node_seq)
    random.seed(0)
    random.shuffle(node_seq)
    return node_seq

（4）定义邻域生成算子

这里主要定义三类算子：

算子1：单节点交换，即将nodes_seq序列前半部分与后半部分对应位置的需求节点交换；
算子2：双节点交换，即将nodes_seq序列前半部分紧邻两个位置的需求节点与对应的后半部分紧邻位置的需求节点交换；
算子3：指定长度的片段反序；

def createActions(n):
    action_list=[]
    nswap=n//2
    #Single point exchange
    for i in range(nswap):
        action_list.append([1,i,i+nswap])
    #Two point exchange
    for i in range(0,nswap,2):
        action_list.append([2,i,i+nswap])
    #Reverse sequence
    for i in range(0,n,4):
        action_list.append([3,i,i+3])
    return action_list

（5）生成邻域

def doACtion(nodes_seq,action):
    nodes_seq=copy.deepcopy(nodes_seq)
    if action[0]==1:
        index_1=action[1]
        index_2=action[2]
        temporary=nodes_seq[index_1]
        nodes_seq[index_1]=nodes_seq[index_2]
        nodes_seq[index_2]=temporary
        return nodes_seq
    elif action[0]==2:
        index_1 = action[1]
        index_2 = action[2]
        temporary=[nodes_seq[index_1],nodes_seq[index_1+1]]
        nodes_seq[index_1]=nodes_seq[index_2]
        nodes_seq[index_1+1]=nodes_seq[index_2+1]
        nodes_seq[index_2]=temporary[0]
        nodes_seq[index_2+1]=temporary[1]
        return nodes_seq
    elif action[0]==3:
        index_1=action[1]
        index_2=action[2]
        nodes_seq[index_1:index_2+1]=list(reversed(nodes_seq[index_1:index_2+1]))
        return nodes_seq

（6）目标值计算

目标值计算依赖 " splitRoutes " 函数对TSP可行解分割得到车辆行驶路线和所需车辆数， " calDistance " 函数计算行驶距离。

def splitRoutes(nodes_seq,model):
    num_vehicle = 0
    vehicle_routes = []
    route = []
    remained_cap = model.vehicle_cap
    for node_no in nodes_seq:
        if remained_cap - model.node_list[node_no].demand >= 0:
            route.append(node_no)
            remained_cap = remained_cap - model.node_list[node_no].demand
        else:
            vehicle_routes.append(route)
            route = [node_no]
            num_vehicle = num_vehicle + 1
            remained_cap =model.vehicle_cap - model.node_list[node_no].demand
    vehicle_routes.append(route)
    return num_vehicle,vehicle_routes
def calDistance(route,model):
    distance=0
    depot=model.depot
    for i in range(len(route)-1):
        from_node=model.node_list[route[i]]
        to_node=model.node_list[route[i+1]]
        distance+=math.sqrt((from_node.x_coord-to_node.x_coord)**2+(from_node.y_coord-to_node.y_coord)**2)
    first_node=model.node_list[route[0]]
    last_node=model.node_list[route[-1]]
    distance+=math.sqrt((depot.x_coord-first_node.x_coord)**2+(depot.y_coord-first_node.y_coord)**2)
    distance+=math.sqrt((depot.x_coord-last_node.x_coord)**2+(depot.y_coord - last_node.y_coord)**2)
    return distance
def calObj(nodes_seq,model):
    # calculate obj value
    num_vehicle, vehicle_routes = splitRoutes(nodes_seq, model)
    if model.opt_type==0:
        return num_vehicle,vehicle_routes
    else:
        distance=0
        for route in vehicle_routes:
            distance+=calDistance(route,model)
        return distance,vehicle_routes

（7）绘制收敛曲线

def plotObj(obj_list):
    plt.rcParams['font.sans-serif'] = ['SimHei']  #show chinese
    plt.rcParams['axes.unicode_minus'] = False  # Show minus sign
    plt.plot(np.arange(1,len(obj_list)+1),obj_list)
    plt.xlabel('Iterations')
    plt.ylabel('Obj Value')
    plt.grid()
    plt.xlim(1,len(obj_list)+1)
    plt.show()

（8）输出结果

def outPut(model):
    work = xlsxwriter.Workbook('result.xlsx')
    worksheet = work.add_worksheet()
    worksheet.write(0, 0, 'opt_type')
    worksheet.write(1, 0, 'obj')
    if model.opt_type == 0:
        worksheet.write(0, 1, 'number of vehicles')
    else:
        worksheet.write(0, 1, 'drive distance of vehicles')
    worksheet.write(1, 1, model.best_sol.obj)
    for row, route in enumerate(model.best_sol.routes):
        worksheet.write(row + 2, 0, 'v' + str(row + 1))
        r = [str(i) for i in route]
        worksheet.write(row + 2, 1, '-'.join(r))
    work.close()