相机标定 Camera Calibration

相机标定 Camera Calibration

将相机抽象成针孔模型进行建模，同时因为透镜的存在，光线投影到成像平面的过程中会产生畸变(distortion)

相机标定的目的：寻找像素坐标系到世界坐标系之间的转换关系。

相机标定标什么？

相机内参：f_x f_y c_x c_y f(这个可以已知，可能和d_x d_y 包含到f_x f_y) 畸变项：k₁ k₂ k₃ p₁ p₂

相机外参：R T

四个坐标系与针孔模型

相机针孔模型

camera pinhole model

• 成像平面(image plane)：相机的CCD平面，图像在这个平面上形成，注意后续讨论的image plane一般会是指的呈现正像的那个平面Virtual image plane。
• Focal lenth 相机焦距

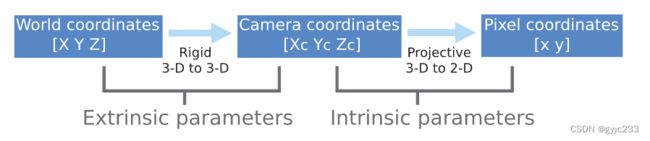
四个坐标系

相机标定涉及以下四个坐标系

• 世界坐标系world coordinate (x_w,y_w,z_w)，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。
• 相机坐标系camera coordinate (x_c,y_c,z_c)，原点位于镜头光心处（针孔模型中的针孔），x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。
• 图像坐标系：物理成像平面，原点是相机光轴与成像平面的交点，是图像的中心点，坐标用x,y表示
• 像素坐标系：是图像像素坐标，($u$,$v$)表示，原点在图像左上角

世界坐标系到相机坐标系转换

[ X c Y c Z c 1 ] = [ R t 0 1 ] [ X w Y w Z w 1 ] \begin{bmatrix}{X_{c}}\\{Y_{c}}\\{Z_{c}}\\{1}\\\end{bmatrix} =\begin{bmatrix}{R}&{t}\\{0}&{1}\\\end{bmatrix} \begin{bmatrix}{X_{w}}\\{Y_{w}}\\{Z_{w}}\\{1}\\\end{bmatrix} ​Xc​Yc​Zc​1​ ​=[R0​t1​] ​Xw​Yw​Zw​1​ ​

假设物体在空间中的三维点坐标为(X_w,Y_w,Z_w)，通过一个刚体变换（左乘该刚体 rigid 变换），变换到相机坐标系，此时坐标变为(X_c,Y_c,Z_c)。为了满足矩阵乘法，添加了1

相机坐标系到图像坐标系的转换

相机坐标系中的点，根据相似三角形关系，映射到光信后方的成像平面（倒像）。根据虚拟成像平面得到正像。

• 根据比例关系，图像坐标系中点的单位为mm
• 相机坐标系点(X_c,Y_c,Z_c) 图像坐标系点(x,y)

$$\begin{gathered} x/f=X_c/Z_c \\ y/f=Y_c/Z_c \end{gathered}$$

$$\begin{gathered} x=X_c\ast f/Z_c \\ y=Y_c\ast f/Z_c \end{gathered}$$

等式两边配平

[ x y 1 ] = [ f / Z c 0 0 0 0 f / Z c 0 0 0 0 1 / Z c 0 ] [ X c Y c Z c ] \begin{bmatrix}x\\y\\1\end{bmatrix} =\begin{bmatrix}{f/Z_{c}}&0&0&0\\0&{f/Z_{c}}&0&0\\0&0&{1/Z_{c}}&0\end{bmatrix} \begin{bmatrix}{X_{c}}\\{Y_{c}}\\{Z_{c}}\end{bmatrix} ​xy1​ ​= ​f/Zc​00​0f/Zc​0​001/Zc​​000​ ​ ​Xc​Yc​Zc​​ ​

图像坐标系到像素坐标系的转换

像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。我们设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍。

像素坐标单位是pixel，不含有mm这些距离相关的信息。

假设：

• 图像x方向每个像素对应d_x mm的物理距离（在物距为f时），图像y方向每个像素对应d_y mm的物理距离（在物距为f时）
  • 1/d_x 含义： x方向每毫米的像素数
  • 1/d_y 含义： y方向每毫米的像素数
• [c_x,c_y]是图像坐标系原点在像素坐标系下的坐标

$$\{\begin{array}{c}u=c_x+x/d_x\\ v=c_y+y/d_y\end{array}$$

等式两边配平
[ u v 1 ] = [ 1 / d x 0 c x 0 1 / d y c y 0 0 1 ] [ x y 1 ] \begin{bmatrix}u\\v\\1\end{bmatrix} =\begin{bmatrix} 1/{d_{x}}&0&{c_{x}}\\ 0&1/{d_{y}}&{c_{y}}\\ 0&0&1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix} ​uv1​ ​= ​1/dx​00​01/dy​0​cx​cy​1​ ​ ​xy1​ ​

世界坐标系到像素坐标系的转换

[ u v 1 ] = [ 1 / d x 0 c x 0 1 / d y c y 0 0 1 ] [ f / Z c 0 0 0 0 f / Z c 0 0 0 0 1 / Z c 0 ] [ R t 0 1 ] [ X w Y w Z w 1 ] \begin{bmatrix} u\\v\\1 \end{bmatrix} =\begin{bmatrix} 1/{d_{x}}&0&{c_{x}}\\ 0&1/{d_{y}}&{c_{y}}\\ 0&0&1 \end{bmatrix} \begin{bmatrix}{f/Z_{c}}&0&0&0\\0&{f/Z_{c}}&0&0\\0&0&{1/Z_{c}}&0\end{bmatrix} \begin{bmatrix}{R}&{t}\\{0}&{1}\\\end{bmatrix} \begin{bmatrix}{X_{w}}\\{Y_{w}}\\{Z_{w}}\\{1}\\\end{bmatrix} ​uv1​ ​= ​1/dx​00​01/dy​0​cx​cy​1​ ​ ​f/Zc​00​0f/Zc​0​001/Zc​​000​ ​[R0​t1​] ​Xw​Yw​Zw​1​ ​

相机内参 intrinsics parameters

将以下矩阵的乘积成为相机内参矩阵intrinsics matrix

• 解释了相机坐标系到像素坐标系的变换关系
• (2)式一般称为内参矩阵

[ 1 / d x 0 c x 0 1 / d y c y 0 0 1 ] [ f / Z c 0 0 0 0 f / Z c 0 0 0 0 1 / Z c 0 ] (1) \begin{bmatrix} 1/{d_{x}}&0&{c_{x}}\\ 0&1/{d_{y}}&{c_{y}}\\ 0&0&1 \end{bmatrix} \begin{bmatrix}{f/Z_{c}}&0&0&0\\0&{f/Z_{c}}&0&0\\0&0&{1/Z_{c}}&0\end{bmatrix} \tag{1} ​1/dx​00​01/dy​0​cx​cy​1​ ​ ​f/Zc​00​0f/Zc​0​001/Zc​​000​ ​(1)

[ f x s c x 0 0 f y c y 0 0 0 1 0 ] (2) \begin{bmatrix} {f_{x}}&s&{c_{x}}&0\\ 0&{f_{y}}&{c_{y}}&0\\ 0&0&1&0 \end{bmatrix} \tag{2} ​fx​00​sfy​0​cx​cy​1​000​ ​(2)

s的定义，普通计算时，一般将s假设为0

相机外参 extrinsics parameters

刚体变换。相机外参矩阵extrinsics matrix 4*4

• 可以用来表示相机在世界坐标系中的位姿

$$\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]$$

畸变模型

由透镜引起的畸变称为径向畸变 Radial distortion

桶形畸变 barrel distortion 越靠近图像中心，图像越被放大

枕型畸变 pincushion distortion 越远离图像中心，图像越被放大

由于透镜与成像平面不平行而导致的畸变成为切向畸变 Tangential Distortion

两种畸变计算(x_distorted, y_distorted)
$$\{\begin{array}{c}{x}_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+[2\ast p_1\ast x\ast y+p_2(r^2+2\ast x^2)]\\ y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+[2\ast p_1\ast (r^2+2\ast y^2)+p_2\ast x\ast y]\end{array}$$
在没有畸变时，相机坐标系到像素坐标系的转换
$$\{\begin{array}{c}u=f_x\ast X_c+c_x\\ v=f_x\ast Y_c+c_y\end{array}$$
引入畸变后
$$\{\begin{array}{c}u=f_x\ast X_{distorted}+c_x\\ v=f_x\ast Y_{distorted}+c_y\end{array}$$

径向畸变模型

坐标点沿着长度方向发生了变化，也就是距离原点的长度发生变化

(x_distorted, y_distorted)

r² = x²+y² (将x,y 转成极坐标表示[r,/σ])

k₁ k₂k₃ 径向畸变系数
$$\{\begin{array}{c}{x}_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\\ y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\end{array}$$

切向畸变模型

坐标点沿着切线方向发生变化，水平夹角发生变化

(x_distorted, y_distorted)

r² = x²+y²
$$\{\begin{array}{c}{x}_{distorted}=x+[2\ast p_1\ast x\ast y+p_2(r^2+2\ast x^2)]\\ y_{distorted}=y+[2\ast p_1\ast (r^2+2\ast y^2)+p_2\ast x\ast y]\end{array}$$

畸变总结

径向畸变 k1 k2 k3

切向畸变 p1 p2

• 实际使用中可以灵活选择畸变模型，如k1 p1 p2 三项

去畸变 undistort

• 将整张图片进行去畸变处理，得到去畸变图像（更常用）
• 从畸变图像某个点出发，按照畸变模型，找到去畸变后的点

圆点与棋盘格

结论： 圆点标定板的标定精度优于棋盘格

圆点标定板：中心拟合精度高，但是存在偏心误差问题。

• 圆的中心的投影，不等于投影出的圆的中心

棋盘格标定板：中心拟合精度低，但是不存在偏心误差问题

圆环的优化方法：

• 将椭圆通过透视投影，投影成正圆
• 检测正圆圆心
• 再将正圆圆心投影回椭圆平面

OpenCV 相机标定

• 让标定板覆盖整个相机平面。永远在中间的话，畸变参数会不准
• 改变角度
• 数量10-20张
• cv::calibrationCamera 返回 重投影误差 这个参数，一般来说，重投影误差越小，表示这次标定精度越好

标定结果的评价

• 重投影误差 re-projection error

• 影响因素：

  • 角点检测精度

  • 相机本身噪声，相机固定

  • 相机分辨率，其他条件相同，分辨率高的话，re-projection error可能会更大（单位是像素）

  • 相机本身的标定算法的最优化

其它思路：

1. 通过图像上某两个角点反向投影到3D空间，计算距离，与其实际物理距离进行比较

相机内参标定后的应用

PnP问题

solvePnP

已知n点之间的对应关系，怎么求它们之间的关系。

已知3D点，对应2D角点，图像坐标系到像素坐标系的变换，畸变参数，去求某一张图片的外参

其它

• 使用背光板
• 过渡带越长，越影响检测

• 快门时间调低，光圈调小