【lstm预测】基于灰狼优化算法改进的lstm预测matlab源码

1 简介

为了解决短期负荷预测精度低,准确性差等问题,采用一种使用灰狼优化算法(GWO)优化长短期记忆网络(LSTM)的短期负荷预测模型.针对模型的参数较难选择的问题,利用GWO对LSTM模型参数寻优.通过实例验证了预测模型的有效性,结果表明GWO-LSTM比LSTM模型具有更好的效果.

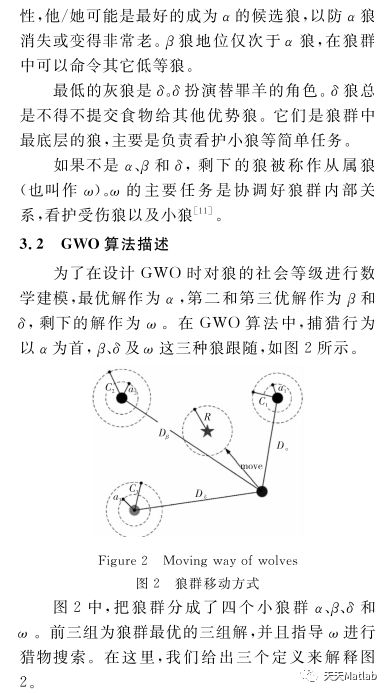
1.1 灰狼优化算法

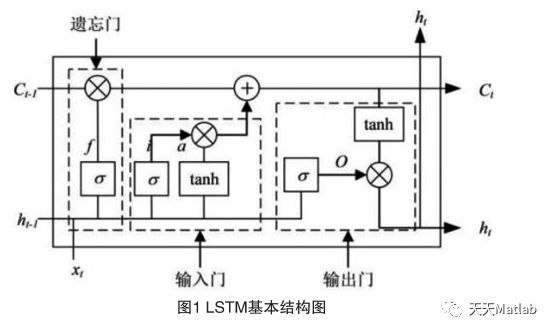
1.2 LSTM模型

1.3 基于鲸鱼算法优化LSTM流程

2 部分代码

%% Get cuckoos by ramdom walk

function nest=get_cuckoos(nest,best,Lb,Ub)

% Levy flights

n=size(nest,1);

% Levy exponent and coefficient

% For details, see equation (2.21), Page 16 (chapter 2) of the book

% X. S. Yang, Nature-Inspired Metaheuristic Algorithms, 2nd Edition, Luniver Press, (2010).

beta=3/2;

sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);

for j=1:n,

    s=nest(j,:);

    % This is a simple way of implementing Levy flights

    % For standard random walks, use step=1;

    %% Levy flights by Mantegna's algorithm

    u=randn(size(s))*sigma;

    v=randn(size(s));

    step=u./abs(v).^(1/beta);

  

    % In the next equation, the difference factor (s-best) means that 

    % when the solution is the best solution, it remains unchanged.     

    stepsize=0.001*step.*(s-best);

    % Here the factor 0.01 comes from the fact that L/100 should the typical

    % step size of walks/flights where L is the typical lenghtscale; 

    % otherwise, Levy flights may become too aggresive/efficient, 

    % which makes new solutions (even) jump out side of the design domain 

    % (and thus wasting evaluations).

    % Now the actual random walks or flights

    s=s+stepsize.*randn(size(s));

   % Apply simple bounds/limits

   nest(j,:)=simplebounds(s,Lb,Ub);

end

% Application of simple constraints

function s=simplebounds(s,lb,ub)

Flag4ub=s>ub;

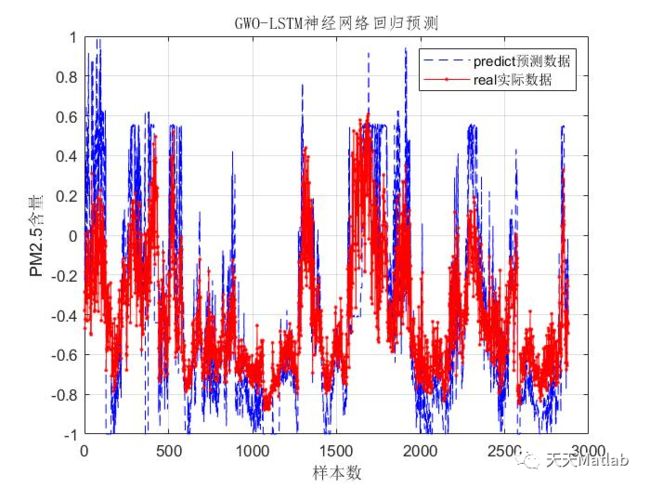
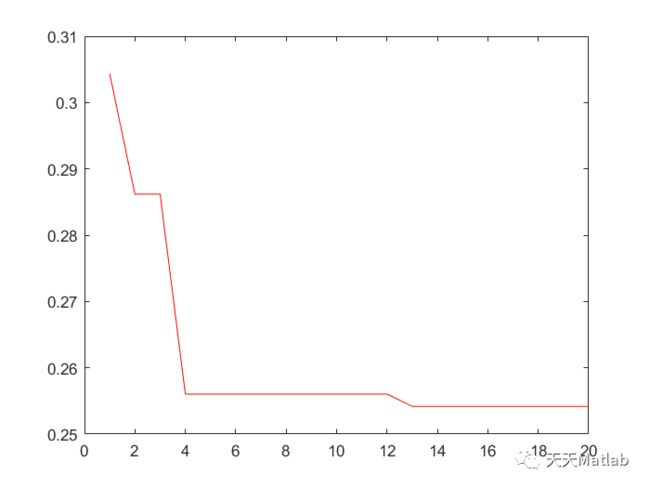
Flag4lb=s

s=s.*(~(Flag4ub+Flag4lb))+ub.*Flag4ub+lb.*Flag4lb;

  % Apply the lower bound

%   ns_tmp=s;

%   I=ns_tmp

%   ns_tmp(I)=Lb(I);

%   

%   % Apply the upper bounds 

%   J=ns_tmp>Ub;

%   ns_tmp(J)=Ub(J);

%   % Update this new move 

%   s=ns_tmp;

3 仿真结果

4 参考文献

[1]曹开田, 高莘尧, 姜梦彦. 一种基于鲸鱼算法优化LSTM的频谱感知方法:.

[2]刘昊东, 邹必昌. 基于鲸鱼算法优化长短期记忆网络的短期负荷预测[J]. 电子世界(3):2.