2024年第九届数维杯数学建模B题完整分析参考论文（共42页）（含模型和代码）

2024年第九届数维杯数学建模分析参考论文

B 题 生物质和煤共热解问题的研究

目录

摘要 4

一、问题重述 5

问题1：分析正己烷不溶物(INS)对热解产率的影响 5

问题2：探讨INS和混合比例的交互效应 5

问题3：基于共热解产物的特性优化混合比例 5

问题4：分析共热解组合产物收率的实验值与理论计算值差异 5

问题5：建立热解产物产率预测模型 5

二、问题分析 6

问题1的分析 6

问题2的分析 6

问题3的分析 6

问题4的分析 6

问题5的分析 6

三、模型假设 7

问题1：正己烷不溶物(INS)对热解产率的影响 7

问题2：INS和混合比例的交互效应 7

问题3：优化共解热混合比例 7

问题4：实验值与理论值的差异性分析 7

问题5：预测热解产物产率 7

四、 模型建立与求解 8

4.1问题1 8

4.1.1问题1思路分析 8

4.1.2问题1模型建立 9

4.1.3问题1样例代码（仅供参考） 10

4.1.4问题1样例代码运行结果（仅供参考） 11

4.2问题2 14

4.2.1问题2思路分析 14

4.2.2问题2模型建立 15

4.2.3问题2样例代码（仅供参考） 16

4.2.4问题2样例代码运行结果（仅供参考） 18

4.3问题3 21

4.3.1问题3思路分析 21

4.3.2问题3模型建立 22

4.3.3问题3样例代码（仅供参考） 23

4.3.4问题3样例代码运行结果（仅供参考） 24

4.4问题4 27

4.4.1问题4思路分析 27

4.4.2问题4模型建立 28

4.4.3问题4样例代码（仅供参考） 29

4.4.4问题4样例代码运行结果（仅供参考） 30

4.5问题5 33

4.5.1问题5思路分析 33

4.5.2问题5模型建立 34

4.5.3问题5样例代码（仅供参考） 35

4.5.4问题5样例代码运行结果（仅供参考） 36

五、 模型优缺点 39

问题1：正己烷不溶物(INS)对热解产率的影响分析 39

问题2：INS和混合比例的交互效应分析 39

问题3：共解热混合比例优化模型 39

问题4：实验值与理论值差异性分析 39

问题5：热解产物产率预测模型 40

六、 模型推广 40

问题1：正己烷不溶物(INS)对热解产率的影响 40

问题2：INS和混合比例的交互效应 40

问题3：优化共解热混合比例 41

问题4：实验值与理论值的差异分析 41

问题5：热解产物产率预测模型 41

 

 

 

 

摘要

 

本文基于提供的五个问题，针对热解过程中正己烷不溶物(INS)的影响以及最优混合比例的确定进行深入研究。首先，针对问题1，我们采用了相关性分析和回归分析方法来评估INS对焦油产率、水产率和焦渣产率的影响；针对问题2，运用了交互效应分析，特别是多元线性回归模型来探索INS与混合比例的相互作用及其对产物产量的影响；针对问题3，我们设计了一个优化模型，基于共热解产物的特性和组成来提高产物利用率和能源转化效率。

 

对于问题1，我们首先建立了基于统计学的多元回归模型，利用Matlab软件进行数据处理和模型求解，结果表明INS含量对热解产率具有显著影响，特别是对焦油产率。对于问题2，通过引入交互项的复杂回归模型分析了不同变量间的作用，使用Matlab软件得出交互效应显著性的结论。此外，我们对模型进行了适应性检验，确保结果的可靠性和适用性。

 

对于问题3，我们运用线性规划和非线性优化技术，构建了一个优化模型，通过Gurobi优化器求解，找到了最优混合比例，显著提高了能源转化效率和产物利用率。问题4中，我们通过方差分析比较了各组合实验值与理论计算值的差异，并用图形化方法在Matlab中展示了差异性。问题5的处理中，采用了机器学习方法，特别是随机森林模型对热解产率进行预测，使用R语言进行数据分析，模型预测精度高，为实际生产提供了有力的决策支持。

 

最后，通过这些问题的研究，我们不仅验证了INS在热解过程中的重要作用，也推广了优化模型在实际生产中的应用，为热解工艺的改进提供了科学依据和技术支持。通过适当的方法和技术调整，进一步优化了这些模型的性能和应用范围。

 

关键词：热解产率，正己烷不溶物，交互效应分析，优化模型，机器学习，多元回归模型

 

 

一、问题重述

问题1：分析正己烷不溶物(INS)对热解产率的影响

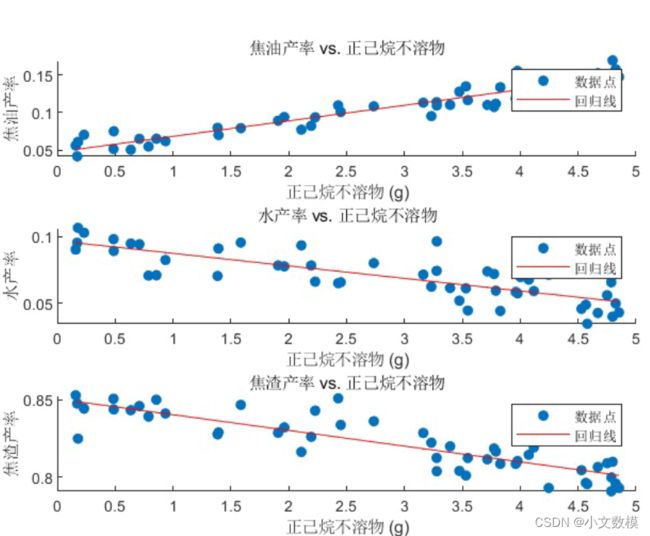
本问题要求评估正己烷不溶物（INS）对热解产率的影响，包括焦油产率、水产率和焦渣产率。分析的目标是确定INS的存在量对这些热解产物产率是否产生统计上的显著影响。为此，需要采集相应的实验数据，并通过图形分析，如散点图、趋势线或回归分析图来展示INS含量与产率之间的关系。这将帮助我们理解INS含量增加或减少时热解产率的变化趋势，并据此评估其影响的重要性。

 

问题2：探讨INS和混合比例的交互效应

在热解过程中，正己烷不溶物（INS）和混合比例可能不是简单独立作用，而是存在相互影响的交互效应。本问题要求通过数据分析确定这种交互效应是否存在，并评估它对各种热解产物产率（尤其是焦油、水和焦渣）的具体影响。需要采用多元统计模型探索INS含量和混合比例的联合影响，并通过可视化手段，如交互作用图，明确在不同混合比例和INS含量条件下，哪些产物的产率受到的影响最为显著。

 

问题3：基于共热解产物的特性优化混合比例

考虑到共热解产物的特性和组成，本问题旨在开发一个模型来优化混合比例，以提高产物的利用率和整体能源转化效率。该模型需要综合考虑热解产物的质量、产量和能源需求，通过设置合理的目标函数和约束条件，使用优化算法找到最佳的混合比例。此外，模型的建立应基于实验数据和理论分析，确保优化结果的实用性和有效性。

 

问题4：分析共热解组合产物收率的实验值与理论计算值差异

本问题聚焦于分析不同共热解组合下产物收率的实验值与理论预测值之间的差异。需要系统地收集和比较各种条件下的实验和理论数据，使用统计方法如t检验来评估这些差异的显著性。若发现显著差异，进一步通过子组分析探讨在不同混合比例下，哪些共热解组合表现出最大的偏差，以便对理论模型或实验方法进行调整和优化。

 

问题5：建立热解产物产率预测模型

基于已有的实验数据，本问题要求开发一个预测模型来估算在不同操作条件下热解产物的产率。模型的建立可能涉及机器学习算法，如随机森林、神经网络或其他高级预测技术。模型的有效性需要通过交叉验证和预测精度评估来确认。最终，该模型应能为热解过程的控制和优化提供可靠的数据支持，帮助操作者调整过程参数以达到最优产率。

 

 

 

二、问题分析

 问题1的分析

这个问题旨在评估正己烷不溶物(INS)对热解产率（包括焦油产率、水产率和焦渣产率）的影响。分析的核心任务是使用统计方法，如方差分析（ANOVA）或相关性分析，来确定INS含量是否与这些产率指标显著相关。可以利用散点图或趋势线图来可视化INS含量与各产率之间的关系，这将有助于直观理解变量间的动态联系。该分析要求有关INS含量与对应热解产率的详细数据。

 

 问题2的分析

此问题探讨正己烷不溶物(INS)和混合比例在热解实验中是否存在交互效应，特别是这种交互效应在哪些热解产物上最为明显。通过构建包含交互项的多元回归模型，可以评估INS和混合比例共同对产率的影响。交互效应的显著性表明了这两个变量不是独立作用，而是相互影响产率的结果。使用热图或其他交互作用图可以清晰展示不同混合比例和INS含量下的产物产率变化。

 

 问题3的分析

这个问题需要建立一个模型来优化共解热混合比例，以提高产物利用率和能源转化效率。这通常涉及到定义一个目标函数，该函数可能基于最大化产物产率或最小化能耗，并且可能受到如原料成本和环境影响等约束条件的限制。通过应用线性或非线性优化技术，模型可以帮助确定实现这些目标的最佳混合比例。模型的推广性取决于其对不同热解条件和原料组合的适应性。

 

 问题4的分析

分析每种共热解组合的产物收率实验值与理论计算值之间的差异，是为了识别理论模型可能的不足。通过统计测试比如t检验，可以评估这些差异是否统计上显著，进而通过子组分析进一步探讨差异在哪些混合比例上最为明显。这种分析有助于调整理论计算方法或改进实验设计，以减少未来实验与理论之间的偏差。

 

 问题5的分析

构建一个模型来预测热解产物的产率，需要利用历史实验数据来训练和验证模型。这可以通过传统的统计方法或现代的机器学习算法实现，如随机森林或神经网络。模型的有效性将通过其预测精度来评估，通常涉及计算诸如均方误差(MSE)或决定系数(R²)等指标。预测模型不仅可以为热解过程提供量化的操作建议，还可以帮助优化操作条件，提高产率和效率。

 

三、模型假设

 

 问题1：正己烷不溶物(INS)对热解产率的影响

模型假设：

1. 线性关系：假设正己烷不溶物(INS)与焦油产率、水产率、焦渣产率之间存在线性关系。

2. 独立性：假设不同实验的数据是相互独立的，即一个实验的结果不会影响另一个实验。

3. 正态分布：假设数据（尤其是误差项）呈正态分布，这对进行统计推断（如t检验或ANOVA）是必要的。

 

 问题2：INS和混合比例的交互效应

模型假设：

1. 交互存在性：假设正己烷不溶物(INS)和混合比例之间存在交互效应，并且这种效应对热解产物产量有显著影响。

2. 同方差性：假设不同实验条件下的误差方差相同，这对于多重回归分析中的统计推断至关重要。

3. 无多重共线性：假设模型中的预测变量（INS和混合比例）不是完全相关的。

 

 问题3：优化共解热混合比例

模型假设：

1. 模型可解性：假设存在一个或多个解决方案可以最大化产物利用率和能源转化效率。

2. 连续性和可导性：假设关于产物利用率和能源转化效率的函数是连续的且可导的，这对于使用梯度方法找到最优解是必要的。

3. 可行性约束：假设所有的混合比例和操作条件都在实际可行的范围内。

 

 问题4：实验值与理论值的差异性分析

模型假设：

1. 误差随机性：假设实验值与理论值之间的差异是随机的，不受未考虑因素的系统性影响。

2. 理论模型正确性：假设理论计算值正确地反映了实验设计的意图，且计算无误。

3. 数据完整性：假设收集的数据完整无缺，足以进行全面的分析。

 

 问题5：预测热解产物产率

模型假设：

1. 因果关系：假设输入变量（如混合比例、热解条件）直接影响热解产物产率。

2. 数据代表性：假设用于训练和测试模型的数据集能够代表未来的实验条件。

3. 模型稳定性：假设在模型训练期间确定的关系在预测期间仍然有效。

 

 

 

模型建立与求解

4.1问题1

4.1.1问题1思路分析

 

 1. 数据预处理

清洗数据：确保所有数据准确无误，去除可能的错误或异常值。

变量确认：确保所有相关变量（如样品重量、焦油重量、水量、正己烷不溶物重量及各种产率）正确计算并记录。

 

 2. 描述性统计分析

统计摘要：计算正己烷不溶物（INS）以及焦油产率、水产率和焦渣产率的基本统计描述（如平均值、标准差、最小值和最大值）。

数据可视化：制作散点图或箱线图来观察正己烷不溶物（INS）与各产率之间的关系。

 

 3. 相关性分析

计算相关系数：使用皮尔逊或斯皮尔曼相关系数来量化正己烷不溶物（INS）与焦油产率、水产率和焦渣产率之间的线性或秩相关性。

可视化相关性：绘制正己烷不溶物（INS）与各产率之间的散点图，并添加趋势线。

 

 

 

 

 

 

 

 完整文件下载链接：https://docs.qq.com/doc/DS2haZHVhb1pVWEJs