FCM模糊聚类算法
如何理解模糊聚类
事物间的界线,有些是明确的,有些则是模糊的。当聚类涉及到事物之间的模糊界线时,需要运用模糊聚类分析方法。
如何理解模糊聚类的“模糊”呢:假设有两个集合分别是A、B,有一成员a,传统的分类概念a要么属于A要么属于B,在模糊聚类的概念中a可以0.3属于A,0.7属于B,这就是其中的“模糊”概念。
模糊聚类分析有两种基本方法:系统聚类法和逐步聚类法。
系统聚类法个人理解类似于密度聚类算法,逐步聚类法类是中心点聚类法。(这里有不对的地方请指正)
逐步聚类法是一种基于模糊划分的模糊聚类分析法。它是预先确定好待分类的样本应分成几类,然后按照最优原则进行在分类,经多次迭代直到分类比较合理为止。在分类过程中可认为某个样本以某一隶属度隶属某一类,又以某一隶属度隶属于另一类。这样,样本就不是明确的属于或不属于某一类。若样本集有n个样本要分成c类,则他的模糊划分矩阵为c×n。
该矩阵有如下特性:
①. 每一样本属于各类的隶属度之和为1。
②. 每一类模糊子集都不是空集。
模糊C-means聚类算法
模糊c-均值聚类算法fuzzy c-means (FCM)。在众多模糊聚类算法中,模糊C-均值(FCM)算法应用最广泛且成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而对样本进行自动分类。
FCM算法原理
假定我们有数据集X,我们要对X中的数据进行分类,如果把这些数据划分成c个类的话,那么对应的就有c个类中心为Ci,每个样本Xj属于某一类Ci的隶属度定为Uij,那么定义一个FCM目标函数及其约束条件如下:
![]()
![]()
目标函数(式1)由相应样本的隶属度与该样本到各类中心的距离相乘组成的,式2为约束条件,也就是一个样本属于所有类的隶属度之和要为 1 。
式1中的m是一个隶属度的因子,一般为2 ,||Xj - Ci|| 表示Xj到中心点Ci的欧式距离。
目标函数J越小越好,说以我们要求得目标函数J的极小值,这里如何求极小值就不推导了(对推导感兴趣的可以看这篇文章:https://blog.csdn.net/on2way/article/details/47087201),直接给出结论:
Uij的迭代公式:
![]()
Ci的迭代公式:
![]()
我们发现Uij和Ci是相互关联的,彼此包含对方,那么问题来了,fcm算法开始的时候既没有Uij也没有Ci,那么如何求解呢?很简单,程序一开始的时候我们会随机生成一个Uij,只要数值满足条件即可,然后开始迭代,通过Uij计算出Ci,有了Ci又可以计算出Uij,反反复复,这个过程中目标函数J一直在变化,逐渐绉向稳定。那么当J不在变化时就认为算法收敛到一个较好的结果了。
Python FCM支持
参考文章:https://blog.csdn.net/FrankieHello/article/details/79581315
安装相关库
pip install -U scikit-fuzzy
skfuzzy.cmeans函数说明
def cmeans(data, c, m, error, maxiter, init=None, seed=None)
参数:
- data:训练数据,这里需要注意data的格式,应为(特征数目,数据个数),与很多训练数据的shape正好相反。
- c:需要指定的聚类个数。
- m:隶属度指数,是一个加权指数,一般为2 。
- error:当隶属度的变化小于此则提前结束迭代。
- maxiter:最大迭代次数。
返回值:
- cntr:聚类中心
- u:最后的隶属度矩阵
- u0:初始化的隶属度矩阵
- d:是一个矩阵,记录每一个点到聚类中心的欧式距离
- jm:是目标函数的优化历史
- p:p是迭代的次数
- fpc:全称是fuzzy partition coefficient, 是一个评价分类好坏的指标,它的范围是0到1, 1表示效果最好,后面可以通过它来选择聚类的个数。
代码实现
import numpy as np
import matplotlib.pylab as plt
from sklearn.cluster import KMeans
from skfuzzy.cluster import cmeans
cp = np.random.uniform(1, 100, (100, 2))
train = cp[:50]
test = cp[50:]
train = train.T
center, u, u0, d, jm, p, fpc = cmeans(train, c=3, m=2, error=0.005, maxiter=1000)
for i in u:
label = np.argmax(u, axis=0)
for i in range(50):
if label[i] == 0:
plt.scatter(train[0][i], train[1][i], c = 'r')
elif label[i] == 1:
plt.scatter(train[0][i], train[1][i], c = 'g')
elif label[i] == 2:
plt.scatter(train[0][i], train[1][i], c = 'b')
plt.show()
运行结果
![]()
FCM算法实现(python)
参考文章:https://blog.csdn.net/a19990412/article/details/89361038
算法流程
-
随机初始化模糊矩阵U(描述每个点在不同类的隶属度)
-
有了模糊矩阵U通过下面公式计算类中心
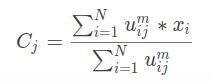
-
通过下面公式根据计算出的类中心,更新模糊矩阵U
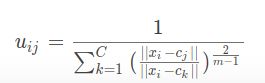
-
当U的变化不大时结束迭代,否则回到第二步
代码实现
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
print(iris.data.shape)
def FCM(X, c_clusters=3, m=2, eps=10):
membership_mat = np.random.random((len(X), c_clusters)) # 生成随机二维数组shape(150,3),随机初始化隶属矩阵
# 这一步的操作是为了使Xi的隶属度总和为1
membership_mat = np.divide(membership_mat, np.sum(membership_mat, axis=1)[:, np.newaxis])
while True:
working_membership_mat = membership_mat ** m # shape->(150,3)
# 根据公式计算聚类中心点Centroids.shape->(3,4)
Centroids = np.divide(np.dot(working_membership_mat.T, X), np.sum(working_membership_mat.T, axis=1)[:, np.newaxis])
# 该矩阵保存所有实点到每个聚类中心的欧式距离
n_c_distance_mat = np.zeros((len(X), c_clusters)) # shape->(150,3)
for i, x in enumerate(X):
for j, c in enumerate(Centroids):
n_c_distance_mat[i][j] = np.linalg.norm(x-c, 2) # 计算l2范数(欧氏距离)
new_membership_mat = np.zeros((len(X), c_clusters))
# 根据公式计算模糊矩阵U
for i, x in enumerate(X):
for j, c in enumerate(Centroids):
new_membership_mat[i][j] = 1. / np.sum((n_c_distance_mat[i][j] / n_c_distance_mat[i]) ** (2 / (m-1)))
if np.sum(abs(new_membership_mat - membership_mat)) < eps:
break
membership_mat = new_membership_mat
return np.argmax(new_membership_mat, axis=1)
print(FCM(iris.data))
代码完全是根据上述流程和公式实现的,理解起来也很简单,迭代退出条件可以优化一下,其他的可以不用改动。
实验数据集
上面代码实验所用的数据集是Iris数据集,该数据集中包含了3种鸢尾花数据,每种50个数据,共150个数据,每个数据包含4个属性:花萼长度,花萼宽度,花瓣长度,花瓣宽度,可以通过这是4个属性预测鸢尾花卉属于哪一类。
数据来源: https://www.kaggle.com/benhamner/python-data-visualizations/data
JAVA实现
参考文章:https://blog.csdn.net/u010498696/article/details/45507071#commentsedit
同样的使用iris数据集,这篇文章的隶属矩阵迭代函数和上面的迭代函数不一样,读者需注意。
实现代码:
import java.io.*;
import java.rmi.server.ExportException;
public class FcmRealize {
private static final String FILE_DATA_IN = "/home/pzs/husin/FCM/iris.data";
private static final String FILE_PAR = "";
private static final String FILE_CENTER = "/home/pzs/husin/FCM/center.data";
private static final String FILE_MATRIX = "/home/pzs/husin/FCM/umaxtrix.txt";
public int numpattern;
public int dimension;
public int cata;
public int maxcycle;
public double m;
public double limit;
public FcmRealize(int numpattern, int dimension, int cata, int maxcycle, double m, double limit){
this.numpattern = numpattern; // 样本数
this.dimension = dimension; // 每个样本点的维度
this.cata = cata; // 需要聚类的类别数
this.maxcycle = maxcycle; // 最大迭代次数
this.m = m; // 参数m
this.limit = limit; // 迭代提前结束条件
}
/**
* 读取样本
* @param pattern 保存iris数据的数组
* **/
public boolean getPattern(double[][] pattern){
BufferedReader br = null;
try{
br = new BufferedReader(new FileReader(FILE_DATA_IN));
}catch (FileNotFoundException e){
e.printStackTrace();
}
String line = null;
String regex = ","; // regex = ","
int row = 0;
while(true){
try{
line = br.readLine();
}catch(IOException e){
e.printStackTrace();
}
if(line == null){
break;
}
String[] split = line.split(regex);
for(int i=0;i maxValue){
maxValue = a[i];
}
}
minmax[0] = minValue;
minmax[1] = maxValue;
return minmax;
}
/**
* 标准化样本,为什么这里要标准化,省略也可以
* @param pattern 样本
* @param numpattern 样本数量
* @param dimension 样本属性个数
* @return
* **/
public static boolean Normalized(double pattern[][], int numpattern, int dimension){
double min_max[] = new double[2];
double a[] = new double[pattern.length];
double copypattern[][] = new double[numpattern][dimension];
for(int i = 0;i= numpattern || m<=1){
return false;
}
// 标准化样本
Normalized(pattern, numpattern, dimension);
int dai = 0, testflag = 0; // 迭代次数,迭代结束标志
// 随机初始化隶属矩阵
double temp[][] = new double[cata][numpattern];
for(int i=0; i f){
f = cha[i][j];
}
}
}
if(f <= 1e-6 || dai>maxcycle){
testflag = 1;
System.out.print("maxcycle : ");
System.out.println(maxcycle);
}
dai += 1;
}
return true;
}
/**
* 输出隶属度矩阵和聚类中心
* @param umatrix
* @param rescenter
* **/
public void Export(double[][] umatrix, double[][] rescenter){
String str = null;
String tab = "\t";
// 矩阵转置,便于在txt中显示
double[][] new_umatrix = new double[numpattern][cata];
for(int i=0; i maxVlue){
maxVlue = new_umatrix[i][j];
maxVlueIndex = j;
}
}
System.out.println(maxVlueIndex);
}
// 输出隶属矩阵
try{
FileWriter maxtrixFileWrite = new FileWriter(FILE_MATRIX);
for(int i=0; i FCM的缺点
FCM是对J目标函数求极小值,也就是说我们得到的结果可能是目标函数的局部极值点或者是鞍点。