TransE模型学习笔记

目录

一、知识表示学习的引入

二、论文摘要

三、方法介绍

（一）建模多关系数据

（二）关系嵌入到向量空间中的翻译

四、TransE模型

（一）学习实体和关系的低维嵌入向量

（二）基于“能量”的计算方法

五、算法流程

（一）算法流程图 

（二）算法伪代码

六、实验

（一）数据集

1. Freebase数据集格式

2. TranE训练数据集格式

 （二）算法实现细节

1. 输入输出

2. L2范式归一化

3. 使用deepcopy函数更新向量

4. 模型参数更新

5. 训练并更新向量的细节

6. 测试环节，将测试集分为Raw及Filter两种情况

7. loss函数的理解

（四）实验设置

1. 评估指标

2. 测试方式

3. 参数设置

4. 构建负样本

（五）链接预测

（六）详细结果

（七）学习预测新关系

七、结论

参考文档

---

今天分享的是NIPS 2013的一篇经典论文《Translating Embeddings for Modeling Multi-relational Data》

原文连接：https://proceedings.neurips.cc/paper/2013/file/1cecc7a77928ca8133fa24680a88d2f9-Paper.pdf

前言：知识图谱又称为科学知识图谱，在图书情报界称为知识域可视化，或知识领域映射地图，用来显示知识发展进程与结构关系的一系列各种不同的图形，用可视化技术描述知识资源及载体，挖掘、分析、构建、绘制和显示知识及他们互相之间的关系。

知识图谱的基础结构是（头实体h,关系r,尾实体t）构成。例如（中国，首都，北京），其中 中国 和 北京 是实体，首都 对应关系。

一、知识表示学习的引入

通常，我们使用三元组(head, relation, tail)来表示知识。在这里，头和尾是实体。例如，(sky tree, location, Tokyo)。我们可以用独热向量来表示这个知识。但实体和关系太多，维度太大。当两个实体或关系很近时，独热向量无法捕捉相似度。受Wrod2Vec模型的启发，我们想用分布表示来表示实体和关系。 

知识表示学习是针对知识图谱的表示学习。表示学习的任务是得到表示主题的低维向量化表示，从而为一些下游任务的计算提供便利，在减少复杂度的同时又能尽可能满足对不同含义的主体进行表征的需求。

知识表示学习学习是将知识图谱中的三元组的元素表示为低维向量。它的下游任务有链接预测和节点分类。

知识图谱数据较网络表示学习面对的数据更为复杂多样，实体和关系类型更为丰富。所以基于数据本身的特性，产生了一些特殊的问题，一些算法只能处理关系简单的数据，而无法处理复杂数据，如具有对称关系、可逆关系的数据。 

二、论文摘要

处理多关系数据大多采用学习潜在特征的方法，模型结构较为复杂且易过拟合。为解决这一问题，作者提出了一种将实体和关系嵌入到低维向量空间中进行计算的建模方法——TransE，该方法较为简单、参数较少，是基于平移距离建模的开山之作。在两个知识库上的实验证明，TransE在链接预测任务中取得了较理想的效果，优于当时的最新方法。

三、方法介绍

本文介绍了一种对多关系数据进行建模的方法。多关系数据是指有向图，节点对应于形式为三元组（头实体，关系，尾实体）（表示为 （h, l, t）），每个三元组都表明实体的头和尾的名称之间存在关系。大型知识库（例如Freebase，Google Knowledge Graph或GeneOntology等）中的知识大多是通过三元组的形式进行表达的。知识库（KB）中的每个实体代表世界的抽象概念或具体的实体，而关系是表示其中两个事实实体的谓词。

本文的工作重点是为知识库（Wordnet和Freebase中的知识库）建立多关系数据建模，目的是提供一种有效的工具，通过自动添加新事实来完成这些数据，而无需额外的知识。下面介绍本文解决的问题和解决方法。

（一）建模多关系数据

本文解决的主要问题在于如何建模多关系型数据。建模关系型数据的困难之处在于无论是实体还是关系都有许多不同的类别并会同时出现，所以对多关系数据建模要用更通用的方法，需要适当的方法来提取出模式。

目前处理多关系数据大多数方法采用的是学习潜在特征的方法。然而大多数模型均较为复杂，会使得正则化项难以设置导致过拟合，过多的局部极小值点带来的非凸优化问题会导致欠拟合。然而有研究表明简单的模型也可以获得很好的结果。

（二）关系嵌入到向量空间中的翻译

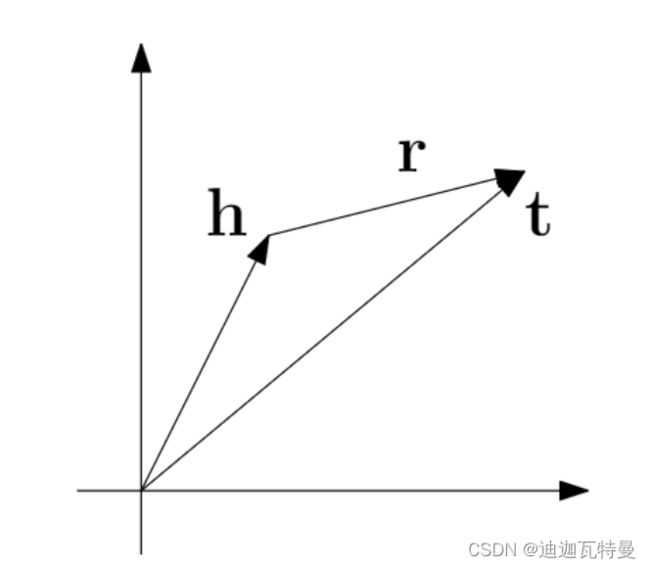
针对以上提出的问题，本文介绍了TransE，一种基于“能量”的模型，用于学习实体和关系的低维嵌入向量。

在TransE中，关系表示为嵌入空间中的平移：对于一组三元组 （h, l, t） ，则头实体 h 的嵌入向量应与尾实体 t 的嵌入向量相加接近于依赖的关系 l 的嵌入向量。本文的模型方法依赖较少的参数，因为它对于每个实体和每个关系仅学习一个低维嵌入向量。 

四、TransE模型

本文提出的TransE模型主要实现学习知识库中实体和关系的低维嵌入向量，然后利用基于”能量”的计算方法，通过对损失函数的梯度进行参数的更新，达到优化的目的。 

（一）学习实体和关系的低维嵌入向量

给定包含多个三元组 （h，l，t） 的训练集 S ，该训练集 S 的每个三元组由两个实体 h ， （实体的集合）和关系   （关系的集合）组成，TransE模型学习实体和关系的向量嵌入，目的是使正确的三元组的嵌入的向量符合   ，否则    则应远离 t 。

（二）基于“能量”的计算方法

对于基于“能量”的框架，每一个三元组的能量等于  ，并且可以将其取为  或  范数。

TransE的损失函数 (Hinge Loss Function) 为:

  

其中    表示    为正时取  、 为负或等于0时取0； γ 是余量超参数，作用相当于是一个正确三元组与错误三元组之前的间隔修正，  γ  越大，则两个三元组之间被修正的间隔就越大，则对于词向量的修正就越严格；并且 

其中     称为打破的三元组（corrupted triplet），是随机替换三元组中的头实体或尾实体得到的，并且头实体和尾实体分别替换，不会同时替换，从而得到打破的三元组。 

可以看出，TransE模型是针对给定三元组进行计算“能量”达到优化目的，其中负例是通过替换头实体或者尾实体自行构造的，优化目标就是使得正负例样本距离最大化，通过最小化正样本的“能量”，最大化负样本的“能量”，达到优化嵌入表示的目的。        

五、算法流程

（一）算法流程图 

TransE的算法流程图下图所示：

（二）算法伪代码

输入：输入的训练集为已经确定三元组集 、实体集、关系集、边缘余量超参数  γ ，嵌入向量的纬度    。

1. 使用uniform 初始化关系    的嵌入向量

2. 对关系    的嵌入向量进行标准化操作

3. 初始化实体   的嵌入向量

4. 开始循环

5. 每一次循环迭代后要对    的嵌入向量进行标准化操作

6. 在   中随机抽取    个三元组作为一个循环迭代的   

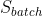
7. 初始化一个空的三元组集   

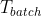
8. 每个  中的三元组进行循环 

9. 对于每个三元组的头实体或尾实体进行打破生成负样本

10. 把正确的三元组和打破的三元组都加入到三元组集  中 

11. 结束循环

12. 通过损失函数的随机梯度下降进行嵌入向量参数的更新

13. 结束循环

六、实验

（一）数据集

• Wordnet：WN18

• Freebase：FB1M、FB15k

1. Freebase数据集格式

 以Freebase数据集为例，Freebase 是一个由元数据组成的大型合作知识库，内容主要来自其社区成员的贡献。它整合了许多网上的资源，包括部分私人wiki站点中的内容。Freebase 致力于打造一个允许全球所有人（和机器）快捷访问的资源库，由美国软件公司Metaweb开发并于2007年3月公开运营。2010年7月16日被Google收购， 2014年12月16日，Google宣布将在六个月后关闭 Freebase ，并将全部数据迁移至Wikidata。Freebase的整体设计很有意思，在知识图谱设计上很具代表性。

Freebase主要来源于开放社区的贡献，包括维基百科Wikipedia、世界名人数据库NNDB、开放音乐数据库MusicBrainz等，目前已经涵盖超过4000中类别、超过7000种属性，截止到2014年年底，包含了6800万个实体，10亿条关系信息，超过24亿条事实三元组信息。

在数据模型的设计上，Freebase不对顶层本体做非常严格的控制，用户可以创建和编辑类和关系的定义。

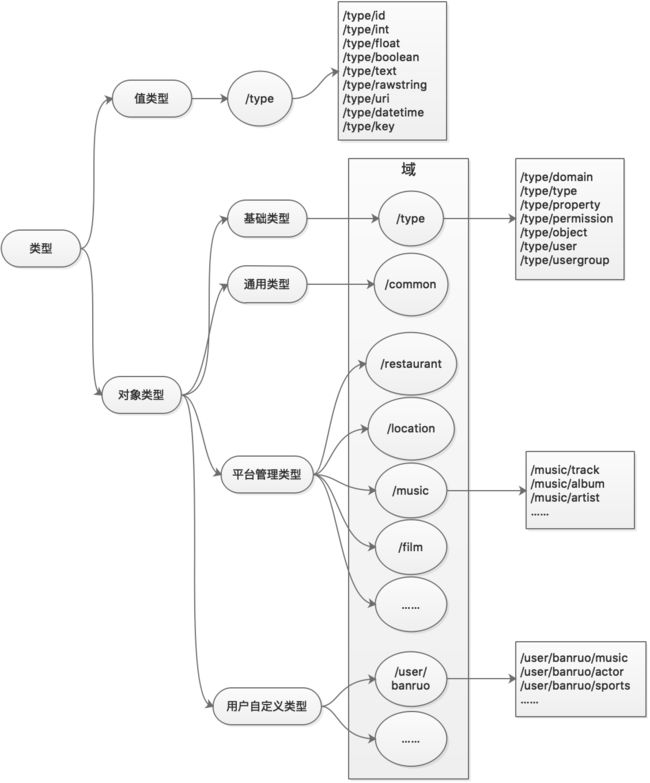
Freebase是个典型的三层结构，FreeBase包含3层结构：Domain-->Type-->Instance(Topic)：People-->Person-->somebody。

例如：

Topic：主题，表示实例或实体，相当于是类的实例化，对应图中的结点，例如物理实体、抽象概念以及思想流派等，比如：姚明。

Type：类型或概念，表示每个Topic所属的类型，可以属于多个Type，对实体进行归类；Domain：域，对类型进行分组，相当于小类对应的大类，便于schema进行管理，比如：人、运动员等。

Domain：域，对类型的分组，便于schema管理，比如：人物。 

Property：属性，表示每个类型或概念所具有的属性类型，每个Type类型都带有一组与该类型相关的不同属性，属性值的类型可以是整型、文本等基本类型，也可以是CVT复合类型，用于表示每个条目由多个字段组成的数据，比如：出生日期、所在球队等。

MID：主题的唯一机器标识符，使用MID对实体进行编号，由 /m 和一个基数为 32 的唯一标识符组成，当主题被合并或拆分时，MID 可以发挥关键作用，允许外部应用跟踪逻辑主题；

属性约束：对属性的取值范围进行约束，比如：类型约束（整型、文本、浮点型、datetime、CVT等）、条件约束（是否单值、是否去重、主属性、逆属性等）。

KEY：可以通过key来唯一确定一个实体，一个实体可以有多个key，每个key都属于一个namespace，比如： "/en/yao_ming"的namespace为"/en"、"/wikipedia/zh-cn_title/姚明" 的namespace为"/wikipedia/zh-cn_title"。对于平台基础模型的实体（Domain、Type、Property），Freebase会从Key中选一个值，作为该实体的ID。 

首先，在Freebase中，每一条信息叫做Topic，也就是一个条目，这就好比字典里的每一个可以查到的词。

然后，每一个Topic包含一个或多个Type（类型），比如"check"这个词，既可以当动词，又可以当名词，于是它就同时属于"动词"和"名词"这两个Type。

接着，每一个Type又包含一个或多个Property（属性），比如字典里的每一个单词的每一种词性，都同时包括读音和释义两部分，因此"读音"和"释义"就是两个property。

最后，每一个属性都有一个值，这个值又是另一个Topic，因此两个Topic就被连接了起来。比如，check当动词时，释义是examine（检查），它本身就是一个Topic，因此这两个词之间就被建立了某种联系。

黄色的方框表示Topic，绿色的方框表示Type。原点"Arnold Schwarzenegger"同时属于四个Type：Person（人物）、Body Builder（健美运动员）、Actor（演员）和Politician（政治家）。Type:Person有一个属性Country of Birth（出生国），它的值是Austria（奥地利）。Type:Politician有一个属性Party（党派），它的值是Republic（共和党）。Type:Actor有一个属性Films（演出的电影），它的值是Terminator（终结者）。 

因此，这里一共有四个Topic：Arnold Schwarzenegger、Austria、Republic、Terminator。它们就这样被连了起来。

通过类型及其配置的属性，可结构化一个Topic，如果Topic属于多个Type，则其结构为这些Type属性的集合。如果属性是基本类型则存储在该topic本身；若是CVT则作为另一个topic存储，通过边进行关联。如下图：橙色部分为模型，蓝色部分为Topic。

Freebase本身就是进行模型schema管理和数据管理的，于是为了足够的灵活性，Freebase平台本身所需的基础模型（Type、Domain、Property、Object）也通过freebase进行自举配置，放在"/type"这个域下，在freebase中只要是"/type"这个域下的都是用于定义平台自身模型的数据，见下图表示的是平台所有类型的分类。

Freebase本身发展了一套数据查询语言MQL，比如我想查出Arnold Schwarzenegger一共演出过多少部电影，查询语句必须这样写：

{
　q0:{
　　query:[{
　　　"name":"Arnold Schwarzenegger",
　　　"type":"/film/actor",
　　　"film":[{
　　　　"film":[{
　　　　　"name":null
　　　　}]
　　　}]
　　}]
　}
}

2. TranE训练数据集格式

（1）entity2id.txt

/m/06rf7	0
/m/0c94fn	1
/m/016ywr	2
/m/01yjl	3
/m/02hrh1q	4
/m/03ftmg	5
/m/04p_hy	6
/m/06151l	7
/m/07vqnc	8
/m/0jn38	9

（2）relation2id.txt 

/people/appointed_role/appointment./people/appointment/appointed_by	0
/location/statistical_region/rent50_2./measurement_unit/dated_money_value/currency	1
/tv/tv_series_episode/guest_stars./tv/tv_guest_role/actor	2
/music/performance_role/track_performances./music/track_contribution/contributor	3
/medicine/disease/prevention_factors	4
/organization/organization_member/member_of./organization/organization_membership/organization	5
/american_football/football_player/receiving./american_football/player_receiving_statistics/season	6
/user/narphorium/people/wealthy_person/net_worth./measurement_unit/dated_money_value/currency	7
/sports/sports_team/roster./soccer/football_roster_position/player	8
/business/company_type/companies_of_this_type	9

（3）train.txt 

/m/027rn	/location/country/form_of_government	/m/06cx9
/m/017dcd	/tv/tv_program/regular_cast./tv/regular_tv_appearance/actor	/m/06v8s0
/m/07s9rl0	/media_common/netflix_genre/titles	/m/0170z3
/m/01sl1q	/award/award_winner/awards_won./award/award_honor/award_winner	/m/044mz_
/m/0cnk2q	/soccer/football_team/current_roster./sports/sports_team_roster/position	/m/02nzb8
/m/02_j1w	/sports/sports_position/players./soccer/football_roster_position/team	/m/01cwm1
/m/059ts	/government/political_district/representatives./government/government_position_held/legislative_sessions	/m/03h_f4
/m/011yn5	/film/film/starring./film/performance/actor	/m/01pjr7
/m/04nrcg	/soccer/football_team/current_roster./soccer/football_roster_position/position	/m/02sdk9v
/m/07nznf	/film/actor/film./film/performance/film	/m/014lc_

 （二）算法实现细节

1. 输入输出

在我刚接触KGE的时候，完全不懂这些数据的格式到底是什么东西，在这里进行简单的介绍：

以FB15K为例：五个文件依次代表实体集合，关系集合，测试集，训练集，验证集。

这里面就只需要把FB15K的实体就当作实体就行了，虽然它是以特殊编码的形式，类似下面这种，第一个是实体名称，后面的是这个实体对应的编号。

其实这里不用关注实体的表现形式是什么样子的，不论是这个文件的这种编码的样子，或者我们平时见到的直接可以看到是什么实体的样子，都是一样的，只要能代表那个实体就行，最后都是转化成对应数字的形式。

模型的输出是实体和关系的向量表示。  

2. L2范式归一化

entity需要在每次更新向量前进行L2范数归一化（除以自己的l2范数），这是通过人为增加embedding的norm来防止Loss在训练过程中极小化。代码中没有完全按照这个规则设置，代码中首先都对实体和关系都进行了初始化和L2范数归一化，然后每训练一个epoch，都对实体和关系进行一次L1范数归一化

范数简单可以理解为用来表征向量空间中的距离，而距离的定义很抽象，只要满足非负、自反、三角不等式就可以称之为距离。采用范式作为正则项，可以防止模型训练过拟合，相关解释可以参考我之前的博文：分类——正则化Python实现_迪迦瓦特曼的博客-CSDN博客_正则化python实现

以及另一篇博文：如何防止我的模型过拟合？这篇文章给出了6大必备方法 

LP范数不是一个范数，而是一组范数，其定义如下：

的范围是[1,∞)。在(0,1)范围内定义的并不是范数，因为违反了三角不等式。

根据的变化，范数也有着不同的变化，借用一个经典的有关P范数的变化图如下：

上图表示了  从0到正无穷变化时，单位球（unit ball）的变化情况。在P范数下定义的单位球都是凸集，但是当  时，在该定义下的unit ball并不是凸集（这个我们之前提到，当时并不是范数）。 

向量的L2范数定义为：

要使得x归一化到单位L2范数，即建立从x到x’的映射，使得x’的L2范数为1。
则：

L2范数归一化后的结果如下图所示，其中绿色点是原始数据点，红色点是L2归一化之后的点，L2归一化之后的数据点全部落在了以原点为中心，半径为1 的圆周上，并且原始数据点和L2归一化之后的点以及原点共线。如果将每个特征维度进行归一化，由于每个维度2范数归一化之后的值肯定会小于1，所以不管原来的特征向量值有多大，2范数归一化的特征向量都在一个半径为1的超球之内，并且可以保持原始特征向量之间的位置关系。

 代码实现如下：

    def data_initialise(self):
        entityVectorList = {}
        relationVectorList = {}
        for entity in self.entities:
            entity_vector = np.random.uniform(-6.0 / np.sqrt(self.dimension), 6.0 / np.sqrt(self.dimension),
                                              self.dimension)
            entityVectorList[entity] = entity_vector

        for relation in self.relations:
            relation_vector = np.random.uniform(-6.0 / np.sqrt(self.dimension), 6.0 / np.sqrt(self.dimension),
                                                self.dimension)
            relation_vector = self.normalization(relation_vector)
            relationVectorList[relation] = relation_vector

        self.entities = entityVectorList
        self.relations = relationVectorList

    def normalization(self, vector):
        return vector / np.linalg.norm(vector)

3. 使用deepcopy函数更新向量

copy()与deepcopy()之间的主要区别是python对数据的存储方式。相关解释可参考：Python中copy()、deepcopy()与赋值的区别(浅复制、深复制)_天山卷卷卷的博客-CSDN博客

首先直接上结论：

—–深复制，即将被复制对象完全再复制一遍作为独立的新个体单独存在。所以改变原有被复制对象不会对已经复制出来的新对象产生影响。 

—–而等于赋值，并不会产生一个独立的对象单独存在，他只是将原有的数据块打上一个新标签，所以当其中一个标签被改变的时候，数据块就会发生变化，另一个标签也会随之改变。

—–而浅复制要分两种情况进行讨论：

1）当浅复制的值是不可变对象（数值，字符串，元组）时和“等于赋值”的情况一样，对象的id值与浅复制原来的值相同。

2）当浅复制的值是可变对象（列表和元组）时会产生一个“不是那么独立的对象”存在。有两种情况：

第一种情况：复制的 对象中无 复杂 子对象，原来值的改变并不会影响浅复制的值，同时浅复制的值改变也并不会影响原来的值。原来值的id值与浅复制原来的值不同。

第二种情况：复制的对象中有 复杂 子对象 （例如列表中的一个子元素是一个列表），如果不改变其中复杂子对象，浅复制的值改变并不会影响原来的值。 但是改变原来的值 中的复杂子对象的值  会影响浅复制的值。

对于简单的 object，例如不可变对象（数值，字符串，元组），用 shallow copy 和 deep copy 没区别

复杂的 object， 如 list 中套着 list 的情况，shallow copy 中的 子list，并未从原 object 真的「独立」出来。也就是说，如果你改变原 object 的子 list 中的一个元素，你的 copy 就会跟着一起变。

又有解释说：

deepcopy的原因我觉得可能是这样，按照代码的结构，正样本和负样本应该是同时更新的，做了deepcopy可以保证两者的更新不会互相打扰，但是两者更新顺序其实可以不用同步。

4. 模型参数更新

原文第3章提到了Loss更新的参数，是所有entities和relations的Embedding数据，每一次SGD更新的参数就是一个Batch中所有embedding的值。

选择L1范数或者L2范数来进行三元组距离的计算是TransE的一个超参数

若选择L2范数，求导方法如下：参考了刘知远组实现中的实现，是先对L2范数求导，逐元素判断正负，为正赋值为1，负则为-1

若选择L1范数，L1 范数在x = 0处不可导，L1范数这东西不能求导，因为它不可微，所以需要使用次微分概念，次梯度与次微分_omadesala的博客-CSDN博客_次微分

求导方法参考了刘知远组实现中的实现，是先对L2范数求导，逐元素判断正负，为正赋值为1，负则为-1 

5. 训练并更新向量的细节

update_embeddings函数中，要对correct triplet和corrupted triplet都进行更新。虽然论文中写做(h,l,t)和(h',l,t')，但两个三元组只有一个entity不同（不同时替换头尾实体），所以在每步更新时重叠实体需要更新两次（和更新relation一样）。例如正确的三元组是（1，2，3），错误的是（1，2，4），那么1和2都需要更新两次，针对正确的三元组更新一次，针对错误的三元组更新一次

6. 测试环节，将测试集分为Raw及Filter两种情况

Filter是指过滤corrupted triplets中在training， validation，test三个数据集中出现的正确的三元组。这是因为只是图谱中存在1对N的情况，当在测试一个三元组的时，用其他实体去替换头实体或者尾实体，这个新生成的反例corrupted triple确可能是一个正确triple，因此当遇见这种情况时，将这个triple从测试中过滤掉，从而得到Filter测试结果。

7. loss函数的理解

如图所示，loss是越训练越小的，d正三元组-d负三元组，会得到一个负数，margin是一个正数，加到一起整体式子就是一个正数。

那么随着loss的减小，d正三元组变小，d负三元组变大，d正三元组-d负三元组这个负数会越来越小，当这个负数的绝对值超过margin的时候，整个式子会变成负数，但是这个式子只取正数，当得到负数的时候就将整个式子置为0，所以正负三元组最大的距离就是margin

margin代表就是他们之间的最大的距离，有了margin就不会让负样本的d是无限大 

（四）实验设置

1. 评估指标

• meanrank：预测排名中的正确预测所在的排名的平均值（正确结果排名之和/总查询次数，越小越好）

• hits@10：预测排名中正确预测排在前10位所占的比例（命中前10的次数/总查询次数，越大越好）

2. 测试方式

• Raw：原始数据直接进行测试

• Filter：将在训练集中出现的打破的三元组进行过滤后进行测试（其动机是我们在测试时通过替换得到的三元组并不一定就是负例，可能恰巧换对了，那么它排名高也是正确的，把当前三元组挤下去也正常。 所以测试时在替换后要检查一下新三元组是否出现在训练集中，是的话就删掉，这就是filter训练方法）

注：Filter测试方式得到的实验结果更为可靠、理想，但是会导致训练速度明显变慢

3. 参数设置

• Wordnet： ，，， 

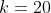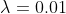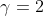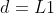
• FB15k： ，，，

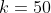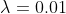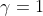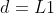
• FB1M： ，，，

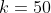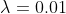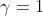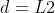
• epoch：1000

4. 构建负样本

创造负样本的时候，这里使计算了平均尾节点数 hpt 和平均头结点数tph

tph 表示每一个头结对应的平均尾节点数

hpt 表示每一个尾节点对应的平均头结点数

当tph > hpt 时 更倾向于替换头实体h，反之则跟倾向于替换尾实体t

举例说明 ：

在一个知识图谱中，一共有10个实体 和n个关系，如果其中一个关系使2个头实体对应5个尾实体，那么这些头实体的平均 tph为2.5，而这些尾实体的平均 hpt只有0.4，

则此时我们更倾向于替换头实体，因为替换头实体才会有更高概率获得正假三元组，如果替换头实体，获得正假三元组的概率为 8/9 而替换尾实体获得正假三元组的概率只有 5/9 

代码实现：

if pr > p:
  # change the head entity
  corrupted_sample[0] = random.sample(self.entities, 1)[0]
  while corrupted_sample[0] == sample[0]:
    corrupted_sample[0] = random.sample(self.entities, 1)[0]
else:
  # change the tail entity
  corrupted_sample[2] = random.sample(self.entities, 1)[0]
  while corrupted_sample[2] == sample[2]:
    corrupted_sample[2] = random.sample(self.entities, 1)[0]

（五）链接预测

链接预测实验结果：

 结果显示了所有数据集的所有方法比较。在原始数据集（raw）和去除错误的三元组之后的数据集（filter）上，TransE均具有较低的 meanrank 和较高的 hits@10 ，在链接预测方面对各种方法有一个清晰的性能评估。

作者认为TransE获得的成就在于其能被高效训练，而其他模型因为复杂所以很难训练，同时嵌入向量很重要。

（六）详细结果

根据关系的几种类别以及预测几种方法的参数对FB15k的结果进行分类（hits@10）：

预测头实体和尾实体时作者将关系分为四类：1-TO-1、1- TO-M ANY，M ANY-TO -1，M ANY-TO-M ANY。如果一个头实体最多可以出现一个尾实体，则给定的关系为1- TO -1；如果一个头实体可以出现很多尾实体，则给定的关系为1- TO -M ANY；如果许多头实体可以出现同一尾实体，则为M ANY-TO -1；如果可以出现多个头实体且带有多个尾实体，则为 M ANY-TO -M ANY 。

可以看出，1-TO-1类型评估较好，而 M -TO - 1 等类型效果不够理想。后续TransH算法改进了这个问题（投影到超平面再进行向量计算）。

部分预测结果展示：

（七）学习预测新关系

作者使用FB15k来测试TransE方法对新事实的泛化能力。

为此，作者随机选择了40个关系并将数据分成两组：一组（FB15k-40rel）包含具有这40个关系的所有三元组，另一组（FB15k-rest）包含剩余的三元组。

• 左图：当训练集越大，TransE的平均排名下降的最快

• 右图：当训练集越大，TransE的 hits@10上升的最快

• 结果：TransE算法对数据集关系预测的效果最好

七、结论

本文提出了一种学习知识库嵌入的新方法，其着力于模型的最小参数化以得到知识图谱的实体和关系的向量表示。作者将其应用于了很大一部分的Freebase知识库，与在两个不同知识库上的竞争方法相比，它非常有效。TransE模型的参数较少，计算的复杂度显著降低，并且在大规模稀疏知识库上也同样具有较好的性能与可扩展性。 

参考文档

1. 讨论班分享-以TransE为基础进行扩展的两个角度 

2. python实现TransE模型 

3. 【经典回顾】NIPS 2013 | TransE 

4. 论文阅读（一）TransE 

5. 从OGB评测看大规模知识图谱表示：从TripleRE、InterHT再到Trans模型赏析 

6. 彻底搞懂机器学习中的正则化 

7. 知识图谱嵌入的Translate模型汇总（TransE，TransH，TransR，TransD） - 菜鸟学院 

8. 知识图谱嵌入：TransE代码及解析（初学者也能看懂） - 知乎 

9. 分类——正则化Python实现_迪迦瓦特曼的博客-CSDN博客_正则化python实现

10. 最大最小值归一化和L2范数归一化总结___Destiny__的博客-CSDN博客_l2归一化 

11. 技术总结：DBpedia、Freebase百科图谱项目构建技术解析 - 知乎

12. Freebase再研究 - 阮一峰的网络日志

13. Freebase 的基本概念 - 知乎 

14. 知识图谱调研-Freebase-阿里云开发者社区