SLAM之回环检测与优化

学习目标：

回环检测的目的及主要作用
回环检测的实现方法及主要优缺点
回环优化的实现方法及主要优缺点

例如：

• 回环检测的目的及主要作用
• 回环检测的实现方法及主要优缺点
• 回环优化的实现方法及主要优缺点

---

回环检测的意义

前端提供特征点的提取和轨迹、地图的初值，而后端负责对所有这些数据进行优化。然而，如果像视觉里程计那样仅考虑相邻时间上的关键帧，那么，之前产生的误差将不可避免地累积到下一个时刻，使得整个SLAM出现累积误差，长期估计的结果将不可靠，或者说，我们无法构建全局一致的轨迹和地图。

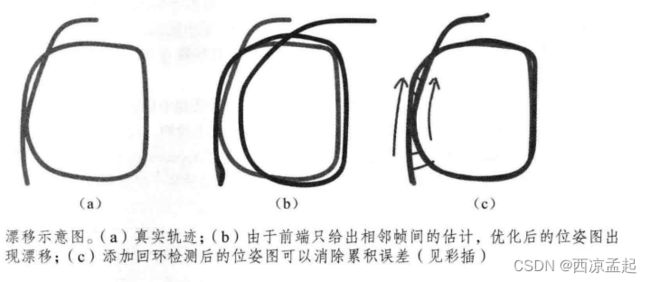
回环检测模块能够给出除了相邻帧的一些时隔更加久远的约束。如果我们能够成功地检测到相机经过同一个地方这件事，就可以为后端的位姿图提供更多的有效数据，使之得到更好的估计，特别是得到一个全局一致的估计。
一方面，回环检测关系到我们估计的轨迹和地图在长时间下的正确性。凌一方面，由于回环检测提供了当前数据与历史数据的关联，我们还可以利用回环检测进行重定位。

回环检测的思路

• 基于里程计(Odometry based)的几何关系
  当我们发现当前相机运动到了之前的某个位置附近时，检测它们有没有回环关系。累积误差较大时无法工作。
• 基于外观(Appearance based)的几何关系
  与前端、后端的估计都无关，仅根据两幅图像的相似性确定回环检测关系。成为视觉SLAM的主流做法。

BRIEF描述子

binary rohust independent elementary features
https://blog.csdn.net/weixin_34910922/article/details/120244876

BRIEF是对已检测到的特征点进行描述，他是一种二进制编码的描述子。BRIEF的特征点位置可利用FAST、Harris检出，或者SIFT、SURF等算法检测特征点的位置，之后使用BRIEF建立特征描述符。

• step1：为减少噪声干扰，先对图像进行高斯滤波(方差为2，高斯窗口为9*9)
• step2：以特征点为中心，取S*S的邻域窗口。在窗口内随机选取一对(两个)点，比较二者像素的大小，进行如下二进制赋值。
  
  其中，p(x)，p(y)分别是随机点x=(u1,v1)，y=(u2,v3)的像素值。
• step3：在窗口中随机选取N对随机点，重复步骤2的二进制赋值，形成一个二进制编码，这个编码就是对特征点的描述，即特征描述子。（一般N=256）
  一对随机点的选择方法，原作者测试了以下5种方法，其中方法(2)比较好。
  
  经过上面的特征提取算法，对于一幅图中的每一个特征点，都得到了一个256bit的二进制编码。

词袋模型DBoW

一种回环检测的思路是：像视觉里程计那样使用特征点来做回环检测，我们对两幅图像的特征点进行匹配，只要匹配数量大于一定值，就认为出现了回环。这种做法存在着一些问题。
词袋，也就是Bag-of-Word(BoW)，目的是用“图像上有哪几种特征”来描述一副图像。

• 确定“人”、“车”、“狗”等概念——对应于BoW中的word，许多单词放在一起，组成了dictionary。
• 确定一副图像中出现了那些在字典中定义的概念——我们用单词出现的情况（或直方图）描述整幅图像。这就把一幅图像转换成一个向量的描述。
• 比较上一步中的描述的相似程度。
  字典是固定的，所以只用一个向量就可以描述整幅图像。
  字典由很多单词组成，而每一个单词代表了一个概念。一个单词与一个单独的特征点不同，它不是从单幅图像上提取出来的，而是某一类特征的组合。所以，字典生成问题，类似于一个聚类(Clustering)问题。
  用k叉树来表示字典。
• 在根节点，用K-means把所有样本聚成k类（实际中为保证聚类均匀性会使用K-means++）。这样就得到了第一层。
• 对第一层的每个节点，把属于该节点的样本再聚成k类，得到下一层。
• 依此类推，最后得到叶子层。叶子层即为所谓的Words。
  
  实际上，最终我们仍在叶子层构建了单词，而树结构中的中间节点仅供快速查找时使用。这样一个k分支、深度为d的树，可以容纳k^d个单词。另外，在查找某个给定特征对应的单词时，只需将它与每个中间节点的聚类中心比较(一共d次),即可找到最后的单词，保证了对数级别的查找效率。
  https://www.cnblogs.com/guoben/p/13339291.html
  DBoW2需要OpenCV和Boost：：dynamic_bitset类才能使用Brief版本。
  DBoW2与DLoopDetector一起在多个真实数据集上进行了测试，执行时间为3毫秒，将图像的Brief特征转换为词袋矢量，执行时间为5毫秒，以在数据库中查找图像匹配项。超过19000张图像。

PnP求解相对位姿

PnP(Perspective-n-Point)是求解3D到2D点对运动的方法。
它描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿。
如果两张图像中的一张特征点的3D位置已知，那么最少只需要3个点对(以及至少一个额外点验证结果)就可以估计相机运动。
特征点的3D位置可以由三角化或者RGB-D相机的深度图确定。
因此，在双目或RGB-D的视觉里程计中，我们可以直接使用PnP估计相机运动。而在单目视觉里程计中，必须先进行初始化，才能使用PnP。3D-2D方法不需要使用对极约束，又可以在很少的匹配点中获得较好的运动估计，是一种最重要的姿态估计方法。
PnP问题有很多种求解方法，例如，用3对点估计位姿的P3P、直接线性变换(DLT)、EPnP(Efficient PnP)、UPnP，等等。此外，还能用非线性优化的方式，构建最小二乘问题并迭代求解，也就是万金油式的光束法平差(Bundle Adjustment，BA)。
首先是DLT。考虑这样一个问题：已知一组3D点的位置，以及它们在某个相机中的投影位置，求该相机的位姿。

请注意上图中的T和SE(3)中的变换矩阵T是不同的。
推导过程如下：
考虑某个空间点P，它的齐次坐标为P=（X,Y,Z,1)^T。

t一共有12维，因此最少通过6对匹配点即可实现矩阵T的线性求解，这种方法称为DLT。当匹配点大于6对时，也可以使用SVD等方法对超定方程求最小二乘解。
在DLT求解中，我们直接将T矩阵看成了12个未知数，忽略了它们之间的联系。
最小化重投影误差求解PnP。我们还可以把PnP问题构建成一个关于重投影误差的非线性最小二乘问题。线性方法，往往是先求相机位姿，再求空间点位置，而非线性优化则是把它们都看成优化变量，放在一起优化。这是一种非常通用的求解方式，我们可以用它对PnP或ICP给出的结果进行优化。这一类把相机和三维点放在一起进行最小化的问题，统称为Bundle Adjustment。
我们完全可以在PnP中构建一个Bundle Adjustment问题对相机位姿进行优化。如果相机是连续运动的，也可以直接用BA求解相机位姿。
重投影误差：将3D点的投影位置与观测位置作差。

邻域匹配(searchByBRIEF)

接下来对有相似或重叠的部分的两幅图像进行配准。
特征匹配是利用的汉明距离进行判决：

• step1：两个特征编码对应bit位上相同元素的个数小于128的，一定不是配对的；
• step2：一幅图上特征点与另一幅图上特征编码对应bit位上相同元素的个数最多的特征点匹配成一对。
  优缺点：
• 优点：计算速度快
• 缺点：1、对噪声敏感(因为二进制编码是通过比较具体像素值来判定的)；2、不具备旋转不变性；3、不具备尺度不变性。

PnPRANSAC

opencv中的一个函数可以用来计算旋转和平移矩阵。

快速重定位

FAST_RELOCALIZATION是opencv库中的一个函数。

滑窗优化

https://zhuanlan.zhihu.com/p/92100386
https://blog.csdn.net/lovely_yoshino/article/details/123623151
https://blog.csdn.net/qq_41694024/article/details/124955119
https://guyuehome.com/37309
为什么需要滑窗：
在SLAM过程中，随着关键帧和路标点的增多，后端BA的计算效率会不断下降。为了避免这种情况，便使用滑窗(Sliding window)将待优化的关键帧限制在一定的数量来控制BA的规模。
在滑动窗口中，当窗口结构发生改变，状态变量应该如何变化。区别于全局BA，滑窗的窗口结构变化可以分为以下两部分讨论：

• 在窗口中新增一个关键帧，以及它观测到的路标点；
• 把窗口中的一个旧的关键帧删除，也可能删除它观测到的路标点。

新增关键帧的操作和全局BA相同。
删除旧的关键帧：首先要明确的是，在窗口中删除关键帧的技术并不是字面上的直接删除，而是前面提到的边缘化，因为直接丢掉变量，就导致损失了信息，关键帧可能能更多地约束相邻的关键帧，直接丢掉的方式就破坏了这些约束。但是边缘化也带来了一些问题：首先，边缘化会将被边缘化掉的变量所带有的信息转化为先验增加到H矩阵中(Fill-in)，这样会破坏BA的稀疏结构；而且，在滑动窗口中使用标准的边缘化操作会导致在新窗口中，与被边缘化的变量相关的变量会在不同的线性化点计算雅可比(因为每次BA的线性化点不同)，破坏了系统的一致性。

• Fill-in问题
  无论是全局BA还是滑窗优化，在进行舒尔消元后，H矩阵不可避免地发生了改变，以边缘化掉某些变量。因此舒尔消元操作在下一次线性化前并没有引入先验信息。但在窗口优化中，被边缘化掉变量后在后续不会再进行更新，因此会对相关块Fill-in，产生先验信息，所以需要额外的操作处理先验块。
• 一致性问题
  总的来说，在滑窗边缘化过程中，需要不断迭代计算H矩阵和残差b，而迭代过程中，在窗口中状态变量会被不断更新。但是对于相同状态的两个不同估计被用来计算估计器的雅可比矩阵导致了估计的协方差矩阵掺入了人为的信息，降低了估计的精度，最终导致了一致性问题。

作为主流框架的前端中常用的方法，滑窗优化是很常见的迭代策略。因为随着SLAM系统的运行，状态变量规模不断增大，如果使用滑动窗口，只对窗口内的相关变量进行优化便可以大大减小计算量。
而作为滑窗优化，我们除了创建滑动窗口的存储空间外，我们还要通过边缘化的方法保留滑窗外的状态，我们可以不去优化滑窗外的参数，但也不能直接丢掉，这样会破坏原有的约束关系，损失约束信息。采用边缘化的技巧，将约束信息转化为待优化变量的先验分布，实际上是从一个联合分布中获得变量子集概率分布的问题。
操作步骤：

• vins_estimator/src/factor/marginalization_factor.cpp：边缘化的具体实现；
• vins_estimator/src/estimator.cpp（部分）；
• 函数optimization负责利用边缘化残差构建优化模型
• 函数slidewindoe负责维护滑动窗口

BA&滑动窗口

带有相机位姿和空间点的图优化称为BA，它能有效地求解大规模的定位与建图问题。
这在SfM问题中十分有用，但是在SLAM过程中，我们往往需要控制BA的规模，保持计算的实时性。倘若计算能力无限，那不妨每时每刻都计算整个BA——但是那不符合现实需要。现实条件是，我们必须限制后端的计算时间，比如BA规模不能超过1玩个路标点，迭代次数不超过20次、用时不超过0.5秒，等等。像SfM那样用一周时间重建一个城市地图的算法，在SLAM里不见得有效。
控制计算规模的做法有很多，必如从连续的视频中抽出一部分作为关键帧，仅构造关键帧与路标点之间的BA，于是非关键帧只用于定位，对建图则没有贡献。
即便如此，随着时间的流逝，关键帧的数量会越来越多，地图规模也将不断增长。像BA这样的批量优化方法，计算效率会不断下降。为了避免这种情况，我们需要用一定手段控制后端BA的规模。这些手段可以是理论上的，也可以是工程上的。
例如，最简单的控制BA规模的思路，是仅保留离当前时刻最近的N个关键帧，去掉时间上更早的关键帧。于是，我们的BA将被固定在一个时间窗口内，离开这个窗口的则被丢弃。这种方法称为滑动窗口法。
取这N个关键帧的具体方法可以有一些改变，例如，不见得必须取时间上最近的，而可以按照某种原则，取时间上靠近，空间上又可以展开的关键帧，从而保证相机即使在停止不动时，BA的结构也不至于缩成一团(很明显，这容易导致一些糟糕的退化情况)。如果我们在帧与帧的结构上再考虑得深一些，也可以像ORB-SLAM2那样，定义一种称为“共视图”(covisibility graph)的结构。所谓共视图，就是指那些“与现在的相机存在共同观测的关键帧”构成的图。
于是，在BA优化时，我们按照某此原则在共视图内取一些关键帧和路标进行优化。例如，仅优化与当前帧有20个以上共视路标的关键帧，其余部分固定不变。当共视图关系能够正确构造的时候，基于共视图的优化也会在更长时间内保持最优。
滑动窗口也好，共视图也好，大体而言，都是我们对实时计算的某种工程上的折中。

位姿图

我们发现特征点在优化问题中占据了绝大部分。实际上，经过若干次观测之后，收敛的特征点位置变化很小，发散的外点则已被剔除。对收敛点再进行优化，似乎是有些费力不讨好的。因此，我们更倾向于在优化几次之后就把特征点固定住，只把它们看作位姿估计的约束，而不再实际地优化它们的位置估计。
沿着这个思路继续思考，我们会想到：是否能够完全不管路标而只管轨迹呢？我们完全可以构建一个只有轨迹的图优化，而位姿节点之间的边，可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。不同的是，一旦初始估计完成，我们就不再优化那些路标点的位置，而只关心所有的相机位姿之间的联系。通过这种方式，我们省去了大量的特征点优化的计算，只保留了关键帧的轨迹，从而构建了所谓的位姿图(Pose Graph)。
我们知道，在BA中特征点数量远大于位姿节点。一个关键帧往往关联了数百个关键点，而实时BA的最大计算规模，即使利用稀疏性，在当前的主流CPU上一般也就是几万个点左右。这就限制了SLAM的应用场景。所以，当机器人在更大范围的时间和空间中运动时，必须考虑一些解决方式。要么像滑动窗口法那样，丢弃一些历史数据；要么像位姿图的做法那样，舍弃对路标点的优化，只保留Pose之间的边。此外，如果我们有额外测量Pose的传感器，那么位姿图也是一种常见的融合Pose测量的方法。
位姿图优化中，节点表示相机位姿，而边，则是两个位姿节点之间相对运动的估计，该估计可以来自于特征点法或直接法，也可以来自GPS或IMU积分。
理论上，即使在优化之后，由于每条边给定的观测数据并不一致，误差也不见得近似于零。
了解雅可比求导后，剩下的部分就和普通的图优化一样了。简而言之，所有的位姿顶点和位姿——位姿边构成了一个图优化，本质上是一个最小二乘问题，优化变量为各个顶点的位姿，边来自于位姿观测约束。

滑窗优化

作为主流框架的前端中常用的方法，滑窗优化是很常见迭代策略。因为随着SLAM系统的运行，状态变量不断增大，如果使用滑动窗口，只对窗口内的相关变量进行优化便可以大大减小计算量。
而作为滑窗优化，我们除了创建滑动窗口的存储空间外，我们还要通过边缘化的方法保留滑窗外的状态，我们可以不去优化滑窗外的参数，但也不能直接丢掉，这样会破坏原有的约束关系，损失约束信息。采用边缘化的技巧，将约束信息转化为待优化变量的先验分布，实际上一个从联合分布中获得变量子集概率分布的问题。

图优化

我们看到，前端视觉里程计能给出一个短时间内的轨迹和地图，但由于不可避免的误差累积，这个地图在长时间内是不准确的。所以，在视觉里程计的基础上，我们还希望构建一个尺度、规模更大的优化问题，以考虑长时间内的最优轨迹和地图。不过，考虑到精度与性能的平衡，实际中存在着许多不同的做法。
21世纪视觉SLAM的一个重要进展是认识到了矩阵H的稀疏结构，并发现该结构可以自然、显式地用图优化来表示。
H矩阵的稀疏性是由雅可比矩阵***J(x)***引起的。H矩阵中的非对角部分的非零矩阵块可以理解为其对应的两个变量之间存在联系，或者可以称之为约束。于是，我们发现图优化结构与增量方程的稀疏性存在着明显的联系。

鲁棒核函数

在前面的BA问题中，我们将最小化误差项的二范数平方和作为目标函数。这种直观的做法，存在一个严重的问题：如果出于误匹配等原因，某个误差项给的数据是错误的，我们会把一条原本不应该加到图中的边给加进去，然而优化算法并不能辨别出这是个错误的数据，它会把所有的数据都当作误差来处理。在算法看来，这相当于我们突然观测到了一次很不可能产生的数据。这时，在图优化中会有一条误差很大的边，它的梯度也很大，意味着调整与它相关的变量会使目标函数下降更多。所以，算法将试图优先调整这条边所连接的节点的估计值，使它们顺应这条边的无理要求。由于这条边的误差真的很大，往往会抹平其他正确边的影响，使优化算法专注于调整一个错误的值。
出现这种问题的原因是，当误差很大时，二范数增长得太快。于是就有了核函数的存在。核函数保证每条边的误差都不会大得没边而掩盖其他的边。具体的方式是，把原先误差的二范数度量替换成一个增长没有那么快的函数，同时保证自己的光滑性质(不然无法求导)。因为它们使得整个优化结果更为稳健，所以又叫它们鲁棒核函数(Robust Kernel)。

滤波和优化的区别

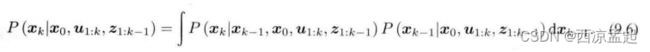
如果考虑更久之前的状态，也可以继续对此式进行展开，但现在我们只关心k时刻和k-1时刻的情况。至此，我们给出了贝叶斯估计，因为上式还没有具体的概率分布形式，所以没法实际操作它。对这一步的后续处理，方法上产生了一些分歧。大体上讲，存在若干种选择：一种方法是假设马尔可夫性，简单的一阶马氏性认为，k时刻状态只与k-1时刻状态有关，而与再之前的无关。如果做出这样的假设，我们就会得到以扩展卡尔曼滤波(EKF)为代表的滤波器方法。在滤波方法中，我们会从某时刻的状态估计，推导到下一个时刻。另一种是依然考虑k时刻状态与之前所有状态的关系，此时将得到非线性优化为主体的优化框架。目前，视觉SLAM的主流为非线性优化方法。
卡尔曼滤波器构成了线性系统的最优无偏估计。
SLAM中的运动方程和观测方程通常是非线性函数，尤其是视觉SLAM中的相机模型，需要使用相机内参模型及李代数表示的位姿，更不可能是一个线性系统。一个高斯分布，经过非线性变换后，往往不再是高斯分布，所以在非线性系统中，我们必须取一定的近似，将一个非高斯分布近似成高斯分布。
卡尔曼滤波器给出了在线性化之后状态变量分布的变化过程。在线性系统和高斯噪声下，卡尔曼滤波器给出了无偏最优估计。而在SLAM这种非线性的情况下，它给出了单词线性近似下的最大后验估计。
由于EKF存在这些明显的缺点，我们通常认为，在同等计算量的情况下，非线性优化能取得更好的效果。这里“更好”是指精度和鲁棒性同时达到更好的意思。

BA

所谓的Bundle Adjustment(BA)，是指从视觉图像中提炼出最优的3D模型和相机参数(内参数和外参数)。考虑从任意特征点发射出来的几束光线(bundles of light rays)，它们会在几个相机的成像平面上变成像素或是检测到的特征点。如果我们调整(adjustment)各相机姿态和各特征点的空间位置，使得这些光线最终收束到相机的光心，就称为BA。

对代价函数最小二乘进行求解，相当于对位姿和路标同时做了调整，也就是所谓的BA。

重力对齐

四元数&俯仰角翻滚角偏航角

第i帧和第j帧的残差

代价函数中的误差项eij描述ki看到pj这件事。

VIO

视觉惯性里程计
visual-inertial odometry

一致性的含义

A recursive estimator is termed consistent when the state estimation errors are zero mean, and their covariance equals the one reported by the estimator.