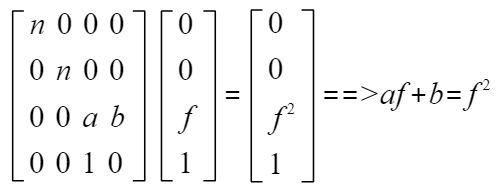3、计算机图形学——模型视图变换、投影变换与视口变换
一、模型视图变换
模型视图变换主要是为了让摄像机回归到世界坐标的原点并且和拍摄物体一起进行变换,便于计算
模型视图变换的根据就是物体和相机的相对位置不变,那么,投影得到的图片也是不变的
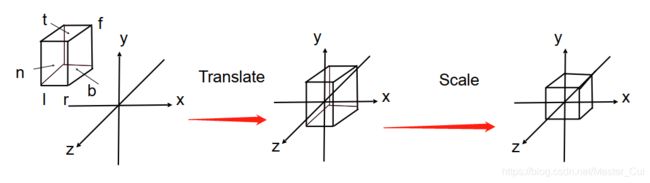
首先规定相机拍摄方向朝向-Z,相机的位置位于e,相机的正上方可以用向量t来表示,那么将相机移动到世界坐标的原点的过程如下图
首先需要将相机平移值世界坐标原点,平移矩阵就可以写成
然后分别需要将g旋转到-Z,将t旋转到Y,将g叉积t的方向旋转到X,然而,这个旋转对应的旋转矩阵并不容易写出,但是如果将Z旋转到-g,将Y旋转到t,将X旋转到g叉积t的方向
那么,这个逆向的旋转矩阵就可以写成
之所以可以这样写,是因为旋转矩阵是正交矩阵,其列向量或列向量可以构成一组正交基向量,而t, -g以及g与t的叉积可以构成一组正交基,所以直接将g与t的叉积方向、t方向与-g方向的三个向量填入旋转矩阵,并且这三个向量可以表示旋转后的向量。于是就有了逆向旋转矩阵
因为旋转矩阵是正交矩阵,所以逆矩阵也是矩阵的转置,所以,此时只需将逆矩阵再次进行转置,就可以得到原来的旋转矩阵
所以,将将g旋转到-Z,将t旋转到Y,将g叉积t的方向旋转到X的旋转矩阵就是逆矩阵的转置
所以,模型视图变换矩阵最终的结果就是
二、投影变换
2.1、正交投影
正交投影假设先把相机移到无穷远处,此时,无论物体离相机多远,投影出来后,物体的大小都是一样的(深度信息被忽略),没有所谓的近大远小的特点,这就是正交投影
2.2、正交投影矩阵
如上图,假设空间中存在一个长方体,最终三个方向均要正交投影到一个标准立方体中,那么首先需要将长方体的中心平移到原点(此时长方体的中心与原点重合,上图画的不太标准),然后该长方体进行一个缩放变换,缩放到标准立方体中,所谓的标准立方体就是在三维坐标中,立方体在XYZ正方向的区域的坐标是(1,1,1),而在XYZ负方向的坐标是(-1,-1,-1),缩放到标准立方体中是为了方便进行后续的视口变换的计算方便。
立方体的坐标表示如下图
所以,平移矩阵可以表示为
平移举例表示中心点要移动的距离,因为是向原点移动,所以需要加负号
平移变换之后,需要进行缩放变换,缩放因子可以表示为
所以,缩放矩阵就可以表示为
所以,最终的正交投影矩阵就是平移矩阵与缩放矩阵的乘积
2.3、透视投影
如下图所示,透视投影并包含深度信息,并因为深度信息而产生近大远小的特点,符合人眼的视觉模型
正交投影中光线的是平行光,而透视投影中的光则是点光源,如下图
2.4、透视投影矩阵
因为透视投影是要通过近大远小表达深度的,而透视投影就是将上图中的棱锥无限切分,然后,全部缩放成近平面的大小。最后,将缩放后的长方体再平移缩放到标准立方体中
所以投影矩阵推导的思路就是:将棱锥模型的四个棱向内挤压内,形成一个长方体,之后将长方体进行一次平移和缩放,使得最终结果处于标准立方体中,也就是说对长方体进行正交投影,最终得到的投影就是透视投影。
将棱锥远平面上的任意一点投影到屏幕后的模型可以表示为
根据相似三角形可得
同理可得
到此,也就是说棱锥内的所有的点的xy坐标都经过了缩放因子为n/z的挤压
所以,变换的形式可以写为
齐次坐标的同乘一个数或者同除以一个不为零的数时,齐次坐标不发生变化,所以,将等号右侧同时乘以z,那么形式就写成
此时,矩阵M可以写成
如何算出pqab这四个值?
首先,棱锥近平面压缩后,近平面上的所有点依然不变,且近平面上的点的z坐标都是n,所以可以得出如下方程
此时,再次利用齐次坐标的不变性,将右边的向量同乘以n,可得
可知,等式右边的结果与xy无关,所以,p=0,q=0
所以,上式最终变为
此外,远平面处的中心点(0,0,f,1)经过挤压后,也没有变化。所以,可以的导入下的方程
联立上述两个方程
最终可得
所以,该转换矩阵可以写为
所以,最终的透视投影矩阵就是该转换矩阵和正交投影矩阵的乘积
三、视口变换
经过了MVP变换,可以将任意三维空间中的物体投影到标准立方体上,但是之后还需要投影到二维平面上进行显示(Z方向暂时不考虑)
所以,就需要将标准立方体中的中的点,转换到屏幕上,所以还是需要先平移,再缩放,形式同正交矩阵
平移分量的符号是正的,是因为中心点远离原点;width/2是缩放因子(从[-1, 1]*[-1, 1]->[0, width]*[0, height])
四、其他概念
4.1、相机的视场(FOV,field of view)
相机的视场分为水平方向和垂直方向,上图表示的是水平方向的视场,视场决定相机的视野的大小
FOV的大小与焦距有关
FOV的大小也与成像平面有关
因为屏幕的尺寸是一定的,所以,如果FOV越大,那么,包含进来的物体就越多,那么,成像后,物体在屏幕中就显得比较小比较拥挤,反之,如果FOV越小,包含的物体就越少,那么,成像后,物体在屏幕中就显得比较大
4.2、屏幕的宽高比(aspect ratio)
屏幕的宽高比决定了图像能否正常显示,如果宽高比过大,那么,出现在屏幕上的画面就会变得矮胖,如果宽高比过小,出现在屏幕上的画面就会变得高瘦,所以,合适的宽高比将会使得图像更好的现实在屏幕上
参考:
GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili
欢迎大家评论交流,作者水平有限,如有错误,欢迎指出