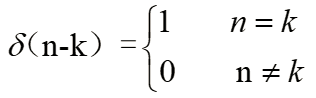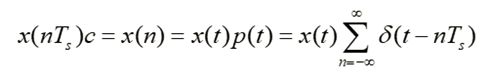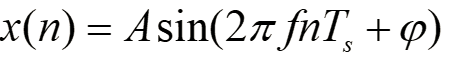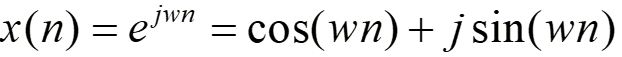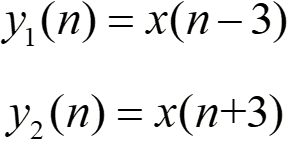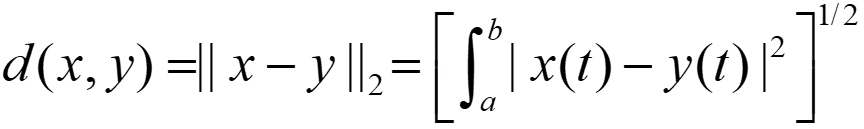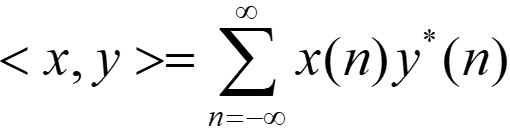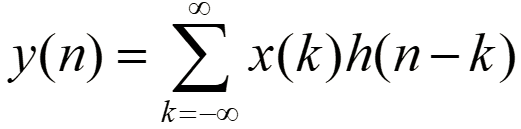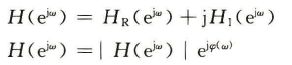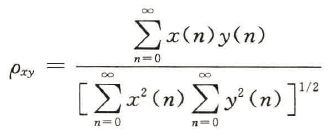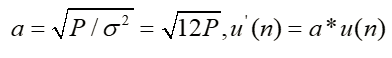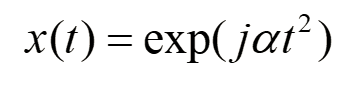数字信号处理1——离散时间系统与常见信号（matlab）

目录

一、信号与系统概念

二、典型信号及运算

三、信号空间

四、LSI线性时不变系统

五、线性卷积

六、LSI系统频率响应

七、相关函数及意义

八、matlab产生信号

---

前言：记录数字信号处理所学理论知识（《数字信号处理理论算法与实现》），以便以后使用时方便查找，也对有需要的童鞋有所帮助

一、信号与系统概念

信号：携带某种信息（一般对我们有用的信息）的物理变量，比如温度压力流量等，可以是电压信号也可也是电流信号；我们描述这样一个信号，使数学函数表示如 x(t)=Asin(2*pi*f*t),函数和信号是通用的，可以说正弦先信号也可以是正弦函数。

模拟信号：若t是定义在时间轴上的连续变量，称为x(t)为连续时间信号，也叫模拟信号

离散信号： t在时间轴上是离散的取值，叫做离散信号

数字信号： 目前DSP芯片以有限位数表示幅度，幅度必须量化即取离散值；那么时间和幅度都是离散值的信号称为数字信号；离散信号和数字信号是通用的。

ADC:模数转换器：两个重要参数：字长和转换速度。字长越长转换精度越高，5V TTL电平使用8bit字长，每一位最大分辨率5V/2^8 转换速度决定了ADC的最大抽样速度；

系统：可以抽象为一种变换或者映射，根据输入序列x(n)变换为输出序列y（n）.表达为 y=T[x(n)];

二、典型信号及运算

2..1单位抽样信号

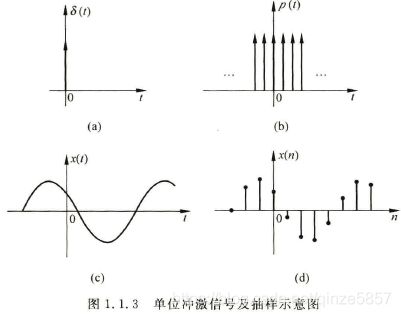
该信号在离散系统种有重要作用，地位犹如冲激响应对于连续系统。在时域上从负到正无穷积分为1。

将δ（n）延迟k个抽样周期，若k从负到正无穷，那么可形成一个无限长的脉冲串序列。

若将连续信号x(t)与脉冲串序列相乘，可以得到离散信号x(nT)，这是连续信号抽样的数学模型

2.2正弦序列及复正弦序列

形如：

f表示频率，单位HZ；W=2*Πf,表示连续角频率，单位rad//s;

式中f_s表示抽样频率

判断离散的正弦信号周期性：如果连续信号x(t)=sin(2pi*f*t)经过抽样得到离散序列x(n)=sin(wn),其周期N应该是一个整数，若sin(wn)=sin(w(n+N))，则认为是周期的。若存在整数r，N,使得 w = 2*pi*r/N成立，则认为是周期的，否则是非周期的。

复正弦序列：

上式称为欧拉公式，它不但是离散信号做傅里叶变换的基函数，也可做为离散系统的特征函数。

2.3指数序列

式中a为常数且|a|<1, 当a是复数，a = re^(jw), 若r<1,其实部和虚部分别是衰减的实余弦和实正弦。

2.4单位阶跃序列

若序列y(n) = x(n)*u(n),那么y(n)的自变量取值就限定在x的右半轴上。

2.5信号操作

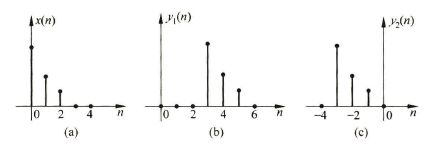
信号时间尺度上加减：信号的延迟，可以记为 左加右减

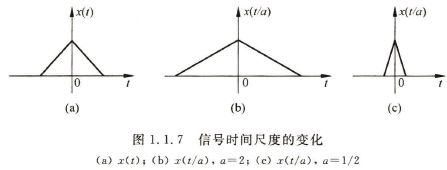
信号时间尺度上乘除：收乘放除，也就是在x轴上收缩a倍 x(a*t),放宽a倍x（t/a）;

信号相加和相乘：表示相同时刻n时的值对应相加或者相乘；标量乘以一个信号表示所有n时刻乘以该常数。

三、信号空间

信号空间元素的度量方法，从不同的角度测量信号的某个特征量，也便于把更多的数学工具引入信号处理中

赋范线性空间：

1范数：信号的绝对值和；2范数：平方和再开根号，表示信号的能量；无穷范数：最大值，表示信号的最大幅度。

度量空间：

任意两个信号x(t), y(t)之间的距离定义为：

内积空间：

若x,y是线性空间X的元素，则定义x，y的内积为：

完备的内积空间称为希尔伯特空间。

四、LSI线性时不变系统

有限冲激响应系统，FIR系统：单位抽样响应为有限长

无限冲激响应系统，IIR系统：抽样响应为无限长

线性系统： 满足叠加原理

时不变系统：若输入x(n)延迟k个抽样周期，输出y(n)也延迟k个抽样周期，即输出与输入时间无关，只要输入信号一样，输出信号的形态保持不变。

五、线性卷积

对于线性时不变（LTI）的离散时间系统，任意信号x(n)通过系统h(n)得到的输出y(n)即为x(n)和h(n)的线性卷积

若x(n)序列是N点，h(n)序列是M点，卷积后序列是N+M-1。计算线性卷积需要四步：反转、平移、相乘、相加。

% 计算两个序列的线性卷积；
%-----------------------------------------------------------------
clear;
N=5;
M=6;
L=N+M-1;
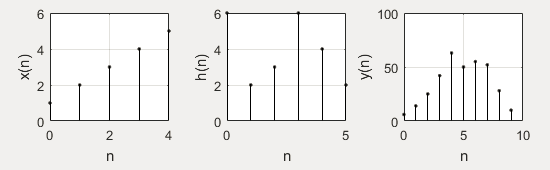
x=[1,2,3,4,5];
h=[6,2,3,6,4,2];
y=conv(x,h);
nx=0:N-1;
nh=0:M-1;
ny=0:L-1;

subplot(231);
stem(nx,x,'.k');xlabel('n');ylabel('x(n)');grid on;
subplot(232);
stem(nh,h,'.k');xlabel('n');ylabel('h(n)');grid on;
subplot(233);
stem(ny,y,'.k');xlabel('n');ylabel('y(n)');grid on;

六、LSI系统频率响应

x(n)为单位抽样信号，输出为单位抽样响应h(n)。 若x(n) = e^(jwn),w为圆频率rad,那么输出y(n)包含了同频率的复正弦信号，但是受H(e^(jw))调制，称为系统的频率响应也叫系统特征值。

|H(e^(jw))|是幅部，称为幅频响应，fai(w)是相位，称为相频响应。

七、相关函数及意义

相关函数：研究两个信号的相似性，或者一个信号经过一段时间延迟后自身的相似性，以实现信号的检测、识别和提取。x(n),y(n)两个能量有限的确定信号，相关系数为：

分母是各自能量乘积开方，是常数，相关系数由分子决定。相关系数等于1表示完全相关，0表示完全无关。

相关函数的意义：进行噪音中信号的检测 ，信号中隐含周期的检测，信号相关性检测等。

白噪声的自相关函数如何理解只有在0处有值？

白噪声的功率谱S(w)=No/2,用图像表示是一个带宽为无限大的一条直线因为功率谱密度跟自相关函数互为一对傅里叶变换 所以R(t)=(No/2)*δ(t)，δ(t)函数只有在t=0时值才为1,为一个冲击,所以只有在t=0时值才不为0。

为什么互为傅里叶对？

% 求两个序列的互相关函数，或一个序列的自相关函数；
%-----------------------------------------------------------------
clear;

N=500;
p1=1;
p2=0.1;
f=1/8;
Mlag=50;
u=randn(1,N);
n=[0:N-1];
s=sin(2*pi*f*n);

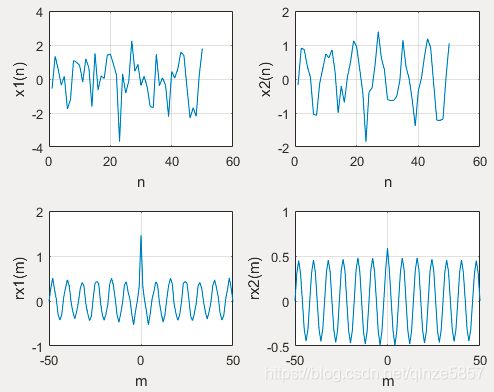
% 混有高斯白噪的正弦信号的自相关
u1=u*sqrt(p1);
x1=u1(1:N)+s;
rx1=xcorr(x1,Mlag,'biased');
subplot(221);
plot(x1(1:Mlag));
xlabel('n');
ylabel('x1(n)');grid on;
subplot(223);
plot((-Mlag:Mlag),rx1);grid on;
xlabel('m');ylabel('rx1(m)');

% 高斯白噪功率由原来的p1减少为p2，再观察混合信号的自相关
u2=u*sqrt(p2);
x2=u2(1:N)+s;
rx2=xcorr(x2,Mlag,'biased');
subplot(222);
plot(x2(1:Mlag));
xlabel('n');ylabel('x2(n)');grid on;
subplot(224);
plot((-Mlag:Mlag),rx2);
grid on;xlabel('m');ylabel('rx2(m)');

八、matlab产生信号

matlab工具箱包含两大类，功能性工具箱和科学性工具箱。功能性工具箱用来扩充MATLAB的符号计算功能、图形可视化功能、建模仿真功能、文字处理功能以及与硬件相关实时交互功能。科学性工具箱按照学科领域分类，如控制工具箱、信号处理工具箱signal processing toolbox、通信工具箱、神经网络工具箱。MATLAB中和信号处理直接有关的工具箱还包括：滤波器设计工具箱filter design toolbox，TI公司DSP开发工具箱develop‘s kit for TIDSP等等。

 

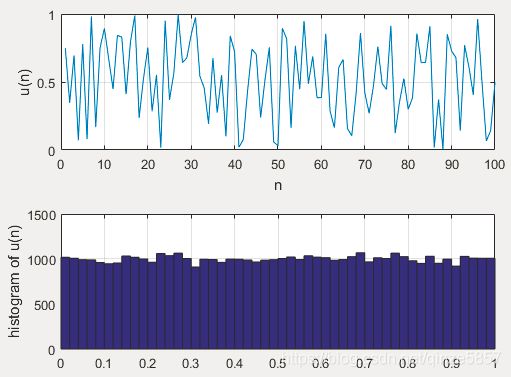
1、rand产生均值为0.5、幅度在0~1之间均匀分布的伪随机数，在DSP中用作均匀分布的白噪声u(n)，功率为1/12

clear;
N=50000;           
u=rand(1,N);       
u_mean=mean(u)     
power_u=var(u)     
subplot(211)       
plot(u(1:100));grid on;
ylabel('u(n)')     
xlabel('n')     
subplot(212)       
hist(u,50);grid on;         
ylabel('histogram of u(n)') 

2.产生一均匀分布、均值为零，功率为0.01的白噪声u（n）。均值为零只需减去平均值，功率为0.01

% 产生均匀分布的白噪信号，使均值为0，功率为p
%-----------------------------------------------------------------
clear;
p=0.01;
N=50000;
u=rand(1,N);
u=u-mean(u);
a=sqrt(12*p); 
u1=u*a;
power_u1=dot(u1,u1)/N  %验证 p=0.01
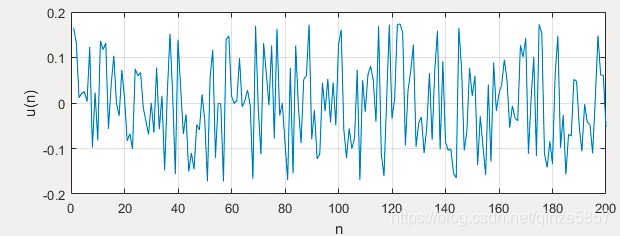
subplot(211)
plot(u1(1:200));grid on;
ylabel('u(n)')     
xlabel('n')   

3. randn产生均值为零，方差为1，服从高斯分布的白噪声u(n)。改变功率的方法与上式相同，将12变为1。如何产生均值为零，功率为0.1，服从高斯分布的白噪声信号u(n)

clear;
p=0.1;
N=500000;
u=randn(1,N);
a=sqrt(p)
u=u*a; 
power_u=var(u)
subplot(211)
plot(u(1:200));grid on;
ylabel('u(n)');
xlabel('n')     
subplot(212)
hist(u,50);grid on; 
ylabel('histogram of u(n)');   

4.产生sinc函数信号，定义sinc(t) =sin(t)/t。离散信号表示为sinc(w)=sin(Nw)/sin(w).w是离散信号的圆频率。该信号比较简单略

5.chirp信号，该信号的基本形式为：

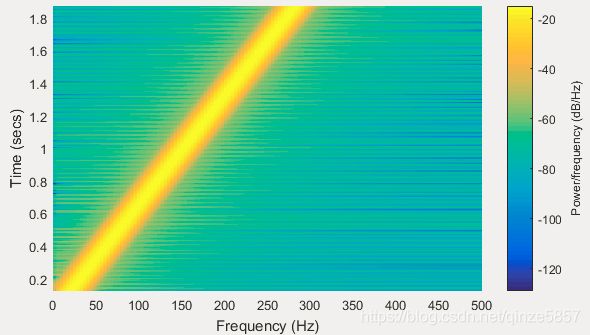
该信号的频率内容是时变的，调用格式x=chirp(T,f0,T1,f1);T表示横轴时间范围向量，F0是起始频率，F1是T1时刻所具有的频率

      t=0:0.001:2;                    % 2 secs @ 1kHz sample rate
      y=chirp(t,0,1,150);             % Start @ DC, cross 150Hz at t=1sec
      plot(t,y)
      spectrogram(y,256,250,256,1E3); % Display the spectrogram

 

参考：

线性卷积的理解： https://blog.csdn.net/baidu_37973494/article/details/83041225