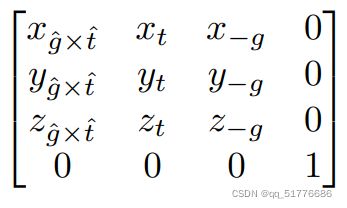计算机图形学笔记二：MVP变换

1.模型变换（Model Transformtion）

是指变换被照物体的位置，角度。即上一节的内容。
目的：是将游戏场景中的物体调整至他们应该在的位置。
简单通俗来讲，就是将场景中的模型摆好，这个过程就叫模型变换。模型变换不同顺序有不同的结果，其实就是因为矩阵相乘不满足交换律，但满足结合律，所以对应同一个复合变换，可以先得出其中的基础变换的矩阵乘积，再与输入向量相乘。一般地，先进行线性变换，再进行非线性变换。

2.视图变换（View Transformation）

也可称为摄像机变换（Camera Tranformation），对于一个三维空间场景（二维亦如此），最终呈现在显示设备上的都是一个二维的平面视图，所以在放置好（模型变换）场景中的模型后，需要找一个合适的角度，让摄像机或者说人眼，看向场景中的被放置好的模型，这个找角度的过程，就叫视图变换。
目的：是得到所有可视物体与摄像机的相对位置。为投影变换做准备。
摄像机定义：视图变换需要对摄像机生成的视图有一个唯一的定义，摄像机定义包含三个要素：
① 位置（Position）：用向量 $e$ 表示：显然，一个物体在空间中，肯定是需要一个坐标的；
② 朝向（Look-at）：用向量 $\hat{g}$ 表示：有了位置后，摄像机不同的拍摄角度会生成不同的视图，所以还要定义一个朝向；
③ 向上的方向（Up direction）：用向量 $\hat{t}$ 表示：即摄像机永远的头的正上方。固定好位置与朝向之后，摄像机还是可以360°旋转的，不同的旋转角也会生成不同的视图，所以还需要定义一个向上的方向来描述摄像机的旋转。

变换方法：
大致思路：将物体和摄像机一起移动，将摄像机的坐标轴移动到x，y，z轴，而物体坐标也作相应的移动。（假设摄像机坐标轴为u,v,w 分别对应原世界空间中的x,y,z）
Step1：将相机位置移动至原点（减去相机位置坐标 $e$ ）
Step2：通过旋转矩阵将二者坐标系重合(用上一节基础变换的方法——旋转矩阵的逆=转置)

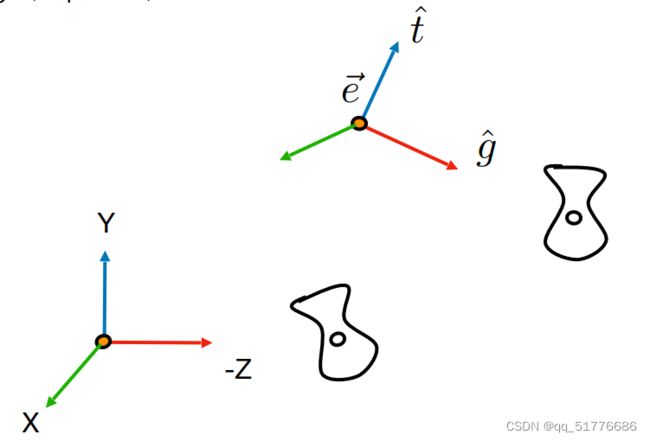
常规步骤：
1.将摄像机位置坐标 $e$ 移动到原点
2.将 $\hat{g}$旋转到-Z
3.将 $\hat{t}$旋转到Y
4.将 $(g\times t)$旋转到X
改进后：
1.将摄像机位置坐标 $e$ 移动到原点
2.由任意位置转换到标准位置改成由标准位置转化为任意位置
3.对求出的矩阵求逆矩阵
4.$M_{view}=R_{view}{T}_{view}$ (顺序不可调换)
第一步：平移矩阵

第二步：旋转矩阵

第三步：求矩阵的逆
旋转矩阵是正交矩阵，所以求矩阵的逆就相当于求该矩阵的转置。

第四步：代入公式计算 $M_{view}=R_{view}{T}_{view}$ (顺序不可调换)

3.投影变换（Project Transformation）

简单来说就是：3D转2D

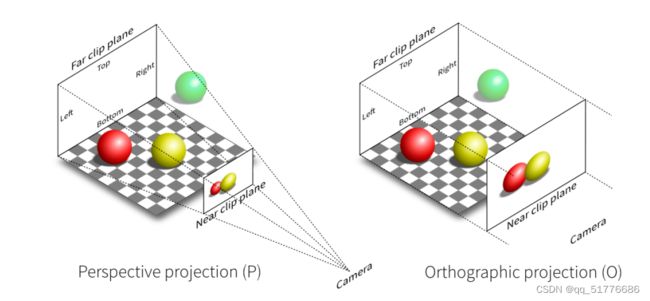
3.1正交投影（Orthographic projection）

概念表示： 正交投影的投影中心到投影面之间的距离是无限远的，当投影中心距离投影面无限远的时候，两个具有前后位置关系的模型看起来大小也是一致的。
数学表示： 正交投影就是摄像机在原点，看向-z方向，顶部在y方向，在看向物体时将所有物体的z值归0，然后将物体平移并缩放到$[-1,1{]}^2$之间。
正交投影的做法就是把物体移到原点处的$[-1,1{]}^3$的标准立方体中。
在变换前，先定义所有模型所在空间的描述：f,n—远/近裁剪平面（Z轴坐标范围）、t,b—上下平面（Y轴坐标范围）、l,r—左右平面（X轴坐标范围）。

变换步骤：
1.将模型中心点平移到原点
2.进行缩放，将模型缩放到$[-1,1{]}^3$的标准立方体中
3.缩放矩阵$\times$平移矩阵
第一步：平移


注：平移矩阵中的这三个平移量得出的原因是因为要将中心平移到原点，所以要取每个轴的中心坐标，平移量为负的原因是将任意一个点平移到原点都是负的平移量。
第二步：缩放

注：缩放矩阵中的这三个缩放量得出的原因是用的$[-1,1]$的标准长度除以物体的每个轴所对应的长度，得到的缩放量。
第三步：相乘

3.2透视投影（Perspective projection）

概念表示： 透视投影的投影中心到投影面之间的距离是有限的，产生了“近大远小”的效果，更符合人眼的成像。欧式几何中规定平行线永不相交，而在透视投影中，平行线会在视觉的“远”处相交。

变换步骤：
1.先将透视投影的几何体“挤”成正交投影的长方体
2.运用解决正交投影变换的方法来解决
第一步：挤

从截面观察各点的变化情况：（结合三角形相似性质）

由此可得出：

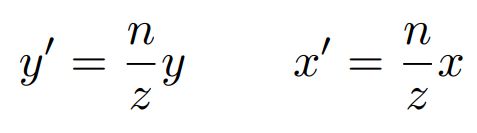
最终远平面“挤压”结果在齐次坐标中：

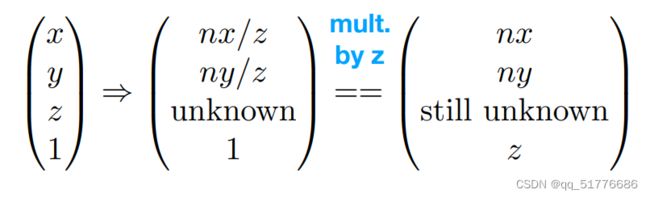
注：乘以z值之后得到的结果仍相同的原因：因为在齐次坐标中，各个维度乘以相同的值得到点和原来一样。
综上所述，可得透视投影“挤压”成正交矩阵的结果为：

由于已经知道了三行的值，所以可以逆推出透视变正交矩阵的三行的值：

推第三行的值：
运用透视投影的性质：

• 近平面上的点坐标不变
• 远平面上的点Z轴坐标不变

注：注意近平面和远平面之间的点Z轴坐标还是会变的
在近平面上：
因为近平面投影后还是自身，即坐标不变，所以如果在近平面上一点 (x, y, n, 1)，与上图的矩阵相乘后，必然会得到 (nx, ny, n², n)，故由 n² 可看出上图中矩阵的第三行 Z 轴的变换与 X,Y 轴无关：

算第三行的大概值：

由上图可得：

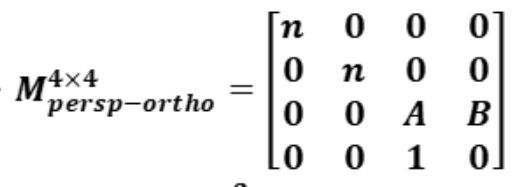
在远平面上：
由这两个性质可得，在远平面上的一点 (x, y, f, 1) ，与上图得到的含A、B的矩阵相乘后，必得 (nx, ny, f², f)，可以得出关于变量 A,B 的关系式，由此可解得四棱台“挤压”到长方体的矩阵：
将远平面上的一点 (x, y, f, 1) 代入：

由上图可得：

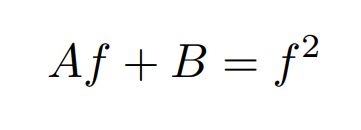
由：
$An+B=n^2$
$Af+B=f^2$
解得：
$A=n+f$
$B=-nf$
代入得：

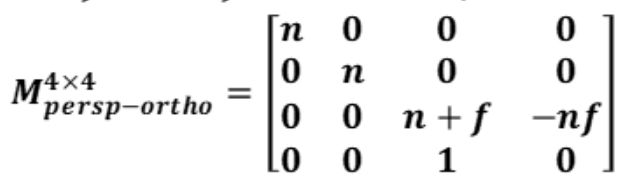
第二步：进行正交投影变换（先平移再缩放）
$M_{persp}=M_{ortho}{M}_{persp\to ortho}$

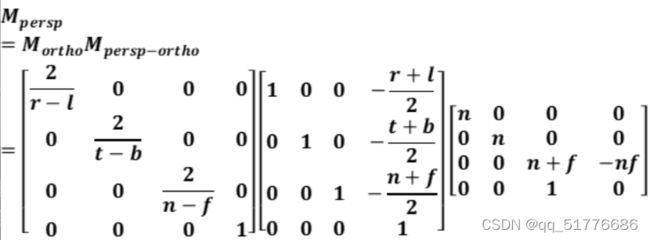
4.视口变换（ViewPort Transformation）

概念表示： 在我们做完投影变换后所有物体都映射在标准坐标系中，但是屏幕会有各种各样的分辨率，所以视口变换是为了将正常设备坐标映射到屏幕坐标。
假设屏幕的宽为width，高度为height，那么视口变换就是把$[-1,1{]}^2$的xy平面变到$[0,width]\times [0,height]$。
注：不考虑Z轴的原因，因为z轴在之后的其他地方有用。