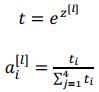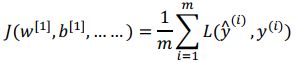深度学习-吴恩达-笔记-7-超参数调试、Batch正则化和程序框架

目录

调试处理

为超参数选择合适的范围

超参数调试实践： Pandas VS Caviar

归一化网络的激活函数

将 Batch Norm 拟合进神经网络

Batch Norm 为什么奏效？

测试时的 Batch Norm

Softmax 回归（ Softmax regression）

训练一个 Softmax 分类器

深度学习框架

TensorFlow

---

【此为本人学习吴恩达的深度学习课程的笔记记录，有错误请指出！】

 

调试处理

---

神经网络涉及到很多的超参数。

 

参数调试的优先级或重要程度如下（从高到低）：

 

学习速率

动量梯度下降法 = 0.9

隐藏层单元数

mini-batch 批次大小

网络层数

学习率衰减

1， 2和

 

注意：参数调试的优先级并不是固定的，只是建议的优先级。

 

随机取值方式：

 

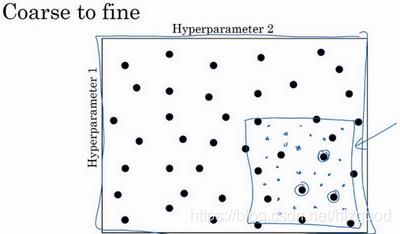
这里假设有两个超参数（左右图都是25的点）。

 

避免采用左图的网格取值方式：这是有规律的取值，参数较少时还好，但不适用参数较多的情况。

 

建议采用右图的随机取值方式：这是随机取样的方式，适合参数较多的情况，如神经网络一般参数都比较多。

 

采用随机取值方式的原因：很多时候，很难提前知道哪个超参数相对重要。假设超参数1比超参数2重要很多（超参数2的取值对算法几乎无效果），如果调试时按照网格取值的方式，那么超参数1最多调试了5个值，虽然一共调试了25次，但最终只有参数1的5个值才对算法产生效果。如果采用随机取值方式，那么超参数1最多调试了25个值，最后从这25个值中选取效果最好的值即可，这种方式增加了超参数的取值数量，也就加大了选到理想的超参数的概率。

 

由粗糙到精细方式：

 

如果采用随机取值方式后，找到了效果最好的点，也许这个点的周围的其它点的效果也很好，那么接下来就放大这个小区域（如小蓝色框内），然后在其中更密集地随机取值，就这样通过不断地由粗略范围到精细范围的调试，最终找到效果最好的值。

 

 

为超参数选择合适的范围

---

在超参数调试中，采用随机取值能有效地找到理想的超参数。有的超参数可以在有效的范围内采取均匀随机取值就能得到较好的效果（如：隐藏层层数、某层的单元数等），但是有的超参数并不适用均匀随机取值（如：学习率 、 等），而是选择合适的标尺来取值。

 

如图：

 

假设超参数 的取值范围在  0.0001 到 1 之间。如果采用均匀随机取值，那 90% 的数值将会落在 0.1 到 1 之间，10% 的数值落在 0.0001 到 0.1 之间。这导致的问题是，90% 的调试集中在 0.1 到 1 之间，只有 10% 的调试集中在 0.0001 到 0.1 之间，所以均匀随机取值不合适了。

 

这里用对数标尺调试超参数的方式会更合理。

 

对数标尺如下：

 

其中 ∈ [-4, 0]， 那么    。

 

所谓对数标尺，也就是对参数的取值范围取对数（这里以10为底数），如：

 

因此 在 [-4, 0] 区间取值分别是 -4、-3、-2、-1、0。超参数 分别取值 0.0001， 0.001， 0.01， 0.1， 1。这样 就有 4 个取值范围，如：0.0001 ~ 0.001、0.001 ~ 0.01、0.01 ~ 0.1、0.1 ~ 1。最后对每个范围均匀随机取值，每个范围的取值数量都变得均匀，而不是都集中在某一个范围里。

 

同样，对 也是采用对数标尺来随机取值。

 

假设 的取值范围在 0.9 到 0.999 区间，那么 1 - 的取值在 0.1 到 0.001 区间，所以我们对 1 - 取对数，也就是 ∈ [-3, -1]，然后对 均匀随机取值：

 

得到：

的取值范围是：0.9 ~ 0.99， 0.99 ~ 0.999。

 

疑问：为什么要用对数标尺取值，而不是线性轴取值？

 

原因是当 、 越接近 1 时，取值对算法的灵敏度变化较大，也就是参数取值每增加一个进位，对结果的影响程度也会增加一个量级。因此，对数标尺取值得到的是每个量级的边界值，根据边界值划分取值范围，然后不断缩小取值范围，找到效果最好的取值。

 

如 从 0.0001 到 0.001，学习速度就会快一个量级。

 

如 在 0.9 到 0.9005 之间取值，两者都是近10天的平均值，所以对结果影响较小。 但 如果在 0.999 到 0.9995 之间取值，前者是近1000天的平均值，后者是近2000天的平均值，所以对结果影响就很大了。因此，取值越靠近 1，对结果的影响就越大。

 

为了直观理解对数标尺取值对结果的影响，以横轴为超参数取值，纵轴为结果的影响程度，如图：

 

从上图看出，每个等级的取值范围大小是一样的，但是它们对应在横轴上取值范围大小是不一样的，我们希望对于不同等级的影响，它们对应在横轴上取值的数量应该是均匀随机的，不应该偏斜到某个等级，而是每个等级的取值数量尽可能的一样。

 

注意： 如果没有在超参数调试中得到正确的标尺取值，影响也不大，只要在均匀的标尺上取值的数量较多，在之后的迭代中，还是会聚焦到有效的超参数取值范围上。

 

 

超参数调试实践： Pandas VS Caviar

---

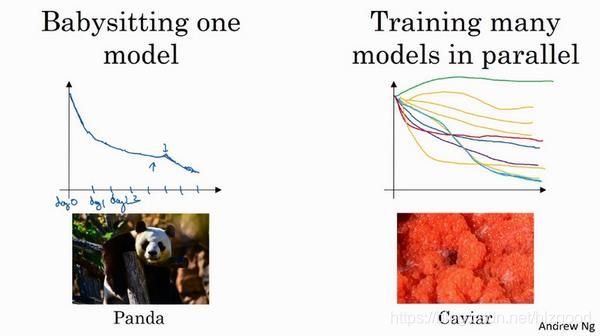
超参数调试实践过程中，通常有两种方式，如图：

 

一种是拥有庞大的训练数据，但是没有足够的计算资源，一次只能调试一个或几个模型。然后接下来的一段时间里，不断地调整超参数，并且观察模型的损失函数的趋势，以便得到一个较好的模型。该方法类似熊猫一样，当熊猫有了孩子，它们的孩子非常少，一次通常只有一个，然后要花费很多精力抚养熊猫宝宝以确保其能成活。

 

另一种是拥有足够的计算资源，在一段较短的时间内，同时试验多种模型，设置了不同的超参数，然后选择损失函数最小的模型。该方法类似鱼子酱， 有些鱼类会产生很多卵，但不对其中任何一个多加照料，只是希望其中一个，或其中一小群，能够表现出色。

 

 

归一化网络的激活函数

---

Batch 归一化使得神经网络对超参数的选择更加稳定， 工作效果也很好。

 

这里有争论的是，到低是在激活函数之前归一化（如对  归一化），还是在激活函数之后归一化（如对  归一化）。

 

通常做法是在激活函数之前归一化。

 

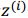归一化过程是，取每一层的  ，先求出均值和方差，然后每个  减去均值再除以标准偏差：

 

为均值、 ^2 为方差，加上是为了数值稳定性。

 

得到的结果  是以平均值为 0，方差为 1 的标准化数据，但是很多时候希望  有不用的分布意义（也就是  的值不是全部集中在一个较小的范围内，这样的激活函数呈线性效果，而是希望它们有较大的方差，就可以更好的利用激活函数的非线性效果），在最终得到的  值如下：

其中， 和  是需要训练出来的参数， 通过对 和 合理赋值，可以构造出以其它平均值和方差的标准化数据。

 

如果   、 =  成立，那么   。

 

因此，神经网络中，不仅要对输入层归一化，对隐藏层也需要归一化。

 

 

将 Batch Norm 拟合进神经网络

---

我们知道了单个隐藏层的 Batch 归一化，深度网络中的 Batch 归一化也是类似的：

 

整个网络中的参数有： 、 、 、 。

 

注意这里的 是Batch归一化的参数，不是高级优化算法（Momentum、Adam、RMSprop）的参数。

 

接下来可以使用梯度下降法或其它高级优化算法来更新每一层的参数。

 

Batch 归一化就是计算均值和方差，然后减去均值，再除以偏差。通常这个计算步骤不用自己手动实现，一些深度学习框架已经实现了 Batch 归一化，如TensorFlow框架中，可以使用函数  tf.nn.batch_normalization 来实现 Batch 归一化。

 

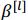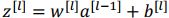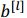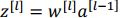实践中，通常使用  mini-batch 下降法来更新整个网络的参数，参数有：  、  、  、  ，z 的计算方式是 ，这里有一个细节，就是可以去掉参数   ，因为在 Batch 归一化的过程中，先要计算   的均值，再减去平均值，  会被消除掉。因此，z 的计算方式可以变成  ，然后再计算 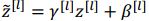 ，最后得到的  中，已经消除了参数  ，转而由 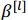 代替来控制偏置条件的影响。

 

最后使用反向传播来更新参数（注意此时已经没有了参数  ）：

 

 

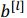Batch Norm 为什么奏效？

---

Batch 归一化有哪些作用？

 

作用一：每一层的输入都经过归一化，相当于对输入进行了特征缩放，这加快了学习速度。

 

作用二：Batch 归一化后，越往后层的权重，越能经受得住输入的变化，也就是提高了模型泛化能力。

 

在前向传播过程中，网络中每一层的输入值都在变化，也就是输入值会存在分布变化较大的问题，经过Batch归一化后，确保 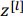   值即使在变化，它的均值和方差都保持不变，也就是 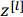  值服从一定的分布，这使输入值经过归一化后变得更稳定。经过一层一层的 Batch 归一化，越往后层的输入值就越稳定，即使输入层的特征值变化较大，也不影响后层网络的适应能力，这也就提高了模型泛化能力。

 

作用三：Batch 归一化有轻微的正则化效果。

 

对于每个 mini-batch，每一层都是基于当前的 mini-batch 来计算均值和方差，而不是在整个数据集上计算均值和方差，所以，由一小部分数据估计出的均值和方差存在一点小噪音，从 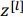   到   的缩放过程也就有一些噪音，这使得后层的单元不过分依赖前层的单元。因为添加的噪音很微小，所以不是巨大的正则化效果，可以把 Batch 归一化和 dropout 一起使用得到强大的正则化效果。

 

注意：不要把 Batch 归一化当成是正则化的方法。

 

 

测试时的 Batch Norm

---

Batch 归一化公式如下：

 

m：表示每一个 mini-batch 中的样本数量。

 

其中均值和方差是通过当前的 mini-batch 中的样本计算得到的，但是在测试时，我们需要通过其它方式来得到均值和方差，因为如果只有一个测试样本的话，一个样本的均值和方差是没有意义的。

 

这里我们使用指数加权平均来估算均值和方差， 这个平均数涵盖了所有 mini-batch。

 

假设有 mini-batch 训练集，如： [1]， [2]， [3]……以及对应的 值，那么：

 

  ：表示 层训练第一个 mini-batch（[1]）得到的均值，

 

  ：表示 层训练第二个 mini-batch（[2]）得到的均值，

 

  ：表示 层训练第三个 mini-batch（[3]）得到的均值等等。

 

然后使用指数加权平均来得到每一层  的最新平均值，使用类似的方式也得到每一层   的最新平均值。

 

最后在测试时，用测试样本得到的  值、指数加权平均得到的  和   、训练中得到的 和 参数，计算出对应的 ̃ 值。

 

 

Softmax 回归（ Softmax regression）

---

对于多分类问题，逻辑回归的做法是对每一类都训练出一个模型，用来判断是否属于该类。神经网络的做法是输出一个n维向量，对应n个分类，该向量只有一个位置为1，其它位置为0，向量中的1表示预测的对应类。

 

通常情况，神经网络的输出的n维向量的元素不是0和1，而是每一个元素是一个概率值，这些元素加起来应该等于1。

 

这里就要用到 Softmax 层，也就是使用 Softmax 激活函数对最后一层（输出层）的  进行计算。

 

假设这里预测的是4个分类：

Softmax 激活函数：

Sigmoid 和 ReLu 的输入是一个实数，输出一个实数，而 Softmax 的输入是一个向量，输出也是一个向量。

 

为了直观理解 Softmax，我们简化网络结构，假设只有输入层和输出层， 两个输入1， 2，输出3个分类。使用训练集训练 Softmax 分类器，得到的是线性的决策边界，如下面是3种情况的训练结果：

 

另一个更多分类的训练结果：

 

对于复杂的神经网络，可以学习更复杂的非线性决策边界，用来区分多种不同的分类。

 

 

训练一个 Softmax 分类器

---

Softmax  使用临时变量 将输出值归一化，是总和为1，如图：

 

Softmax 激活函数 将 Logistic 激活函数推广到 类，而不仅仅是两类，如果 = 2，那么 Softmax 实际上变回了 logistic 回归。

 

如何定义损失函数？

 

假设真实标签、输出预测值是：

在 Softmax 分类中，单个样本的损失函数为：

 

可以看出，真实分类是第二类，但是输出预测值中第二类概率是0.2，这在预测分类中不是最大的概率。梯度下降法为了使损失函数变小， 就需要使 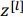 尽可能大，也就是输出的第二类的概率尽可能大。

 

损失函数所做的就是找到训练集中的真实类别，然后试图使该类别相应的概率尽可能地高，这是最大似然估计的一种形式。

 

整个训练集的损失 定义如下：

 

在反向传播过程中，关键的步骤是误差的传播：

 

注意这里得到的误差是一维向量。

 

在使用编程框架中（如：tensorflow、pytorch等），需要自己实现前向传播，编程框架会自动实现反向传播和梯度计算。

 

 

深度学习框架

---

深度学习框架很多，选择适合的即可：

 

 

TensorFlow

---

这里介绍的深度学习框架是 TensorFlow。

 

例子1：优化损失函数 

 

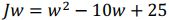
import numpy as np
import tensorflow as tf

#定义变量（参数）
w = tf.Variable(0, dtype = tf.float32)

#定义损失函数
#cost = tf.add(tf.add(w**2, tf.multiply(-10.,w)), 25)
cost = w**2 - 10*w + 25    #也可以直接使用运算符

#定义训练优化器：梯度下降(学习率为0.01，目标是最小化损失)
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

#定义全局变量初始化器
init = tf.global_variables_initializer()

session = tf.Sessions()  #开启一个 TensorFlow session
session.run(init)        #初始化全局变量
print(session.run(w))    #评估变量，输出为0，因为还没开始训练

session.run(train)        #训练一次梯度下降法
print(session.run(w))     #评估变量，输出为0.1

for i in range(1000):     #训练梯度下降 1000 次迭代
    session.run(train)
print(session.run(w))     #评估变量，输出为4.99999，已经接近最优值5

例子2：优化训练集

import numpy as np
import tensorflow as tf

#定义一个[3,1]数组（训练集）
coefficient = np.array([[1.],[-10.],[25.]])    

#定义变量（参数）
w = tf.Variable(0, dtype = tf.float32)

#placeholder函数告诉TensorFlow，稍后会为提供数值
x = tf.placeholder(tf.float32, [3,1])    

#定义损失函数
cost = x[0][0]*w**2 +x[1][0]*w + x[2][0]

#定义训练优化器：梯度下降(学习率为0.01，目标是最小化损失)
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

#定义全局变量初始化器
init = tf.global_variables_initializer()

session = tf.Sessions()  #开启一个 TensorFlow session
session.run(init)        #初始化全局变量
print(session.run(w))    #评估变量，输出为0，因为还没开始训练

session.run(train, feed_dict = {x:coefficients})    #训练一次梯度下降法，指定接入x的数据
print(session.run(w))     #评估变量，输出为0.1

for i in range(1000):     #训练梯度下降 1000 次迭代
    session.run(train, feed_dict = {x:coefficients})
print(session.run(w))     #评估变量，输出为4.99999，已经接近最优值5

TensorFlow 中的 placeholder 是一个之后会赋值的变量，这种方式便于把训练数据加入损失方程。如果使用 mini-batch 梯度下降，在每次迭代时，需要插入不同的 mini-batch，用 feed_dict 来喂入训练集的不同子集。

如果不想用梯度下降法，而是想用 Adam 优化器，只需要修改 tf.train.GradientDescentOptimizer 一行代码即可。

 

TensorFlow 程序的核心是计算损失函数，然后自动计算出导数，以及如何最小化损失，因此代码中定义损失函数所做的就是让 TensorFlow 建立计算图，根据计算损失来实现前向传播和方向传播。