[机器学习导论]——第四课——特征选择
文章目录
- 第四课——特征选择
-
-
- 特征选择动机
- 特征选择方法概述
- 过滤式选择(Filter method)
-
- 单变量过滤
- 多变量过滤
- 包裹式选择(Wrapper method)
- :apple: 嵌入式选择(Embedded method):apple:
-
- 正则化
- 线性回归模型说明
-
- L2正则化——岭回归
- L1正则化——Lasso回归
- 总结
- 参考资料
-
第四课——特征选择
特征选择动机
维数灾难:当维数增大时,空间数据会变得更稀疏,这将导致bias和variance的增加,最后影响模型的预测效果。
对当前学习任务有用的特征称为“相关特征”:所以从众多特征中选择有用的一些特征来进行学习
过拟合:当样本数目小于特征维数时,容易造成过拟合。通过特征选择,可使模型泛化性能好、计算高效、鲁棒可解释
特征选择方法概述
1️⃣ 任务无关方法(过滤式方法):先过滤再训练模型
2️⃣ 任务相关方法(包裹式方法):从众多特征中选取子集,然后使用模型评估特征子集
3️⃣ 自动化方法(嵌入式方法):选择与学习融为一体,模型中暗含了子集选择
过滤式选择(Filter method)
计算代价通常很低,计算速度较快
是特征选择的general框架,与学习器无关(learner-agnostic)
是一个预处理步骤
单变量过滤
单变量(Univariate)过滤方法:Signal-to-noise ratio (S2N)
一个**“好”**的特征:需要有明显的划分度——均值之间有明显的gap
![[机器学习导论]——第四课——特征选择_第6张图片](http://img.e-com-net.com/image/info8/e6c1e7edc24a46abab9f37c59e858738.jpg)
S 2 N = ∣ μ + − μ − ∣ σ + + σ − S2N=\frac{|\mu^+-\mu^-|}{\sigma^++\sigma^-} S2N=σ++σ−∣μ+−μ−∣
单变量过滤方法一些情况下可能失效:需要综合多个特征
多变量过滤
多变量( Multivariate )过滤方法:Relief
给定训练集 { ( x 1 , y 1 ) , . . . , ( x n , y n ) } \{(x_1,y_1),...,(x_n,y_n)\} {(x1,y1),...,(xn,yn)}
1️⃣ 对每个样本xi,在同类样本中赵最近邻 x i , h i t x_{i,hit} xi,hit;在异类样本中寻找最近邻 x i , m i s s x_{i,miss} xi,miss
2️⃣ 计算对应于属性j的统计量
δ j = ∑ i − d i f f ( x i j , x i , h i t j ) 2 + d i f f ( x i j , x i , m i s s j ) 2 \delta^j = \sum_i-diff(x_i^j,x^j_{i,hit})^2+diff(x_i^j,x^j_{i,miss})^2 δj=i∑−diff(xij,xi,hitj)2+diff(xij,xi,missj)2
3️⃣ 若 δ j \delta^j δj大于阈值 τ \tau τ,选择属性j;或者指定一个k值,选择统计量最大的前k 个特征距离是结合多维的特征
包裹式选择(Wrapper method)
Wrapper methods:使用学习器的性能作为评价准则
特征选择结果因学习器不同而不同,选择的特征子集是为学习器“量身定做”
从学习器性能来看,包裹式特征选择方法比过滤式方法好;但是特征选择过程中需多次训练学习器,因此计算开销大。
两个关键问题:
️ Search 搜索特征子集的方法;
️ Assessment 评估特征子集优劣的方法
寻找最优特征子集是一个NP难问题
1️⃣ 使用启发式方法寻找近似候选最优子集
前向选择(Forward Selection):从空集开始,每次增加一个最优特征
算法复杂度: p + ( p − 1 ) + . . . + 1 = p ( p + 1 ) 2 p+(p-1)+...+1=\frac{p(p+1)}{2} p+(p−1)+...+1=2p(p+1) , 为属性的个数
后向消除(Backward Elimination):从全集开始,每次去掉一个最差特征
算法复杂度: p + ( p − 1 ) + . . . + 1 = p ( p + 1 ) 2 p+(p-1)+...+1=\frac{p(p+1)}{2} p+(p−1)+...+1=2p(p+1) , 为属性的个数
2️⃣ 使用验证集或交叉验证方法选择最优子集。
- 将数据划分成训练、验证和测试三部分
- 对每一个特征子集,使用训练集训练模型
- 挑选在验证集上表现最好的特征子集
- 在测试集上进行测试
嵌入式选择(Embedded method)
正则化
在训练过程中隐式进行特征选择,模型只训练一次
只对权重正则化,不对偏置正则化
最常见的嵌入式方法:L1-正则化, L2-正则化,以及L1和L2 混合正则化
1️⃣ L1-正则化
2️⃣ L2-正则化
3️⃣ L1-L2混合正则化
线性回归模型说明
给定训练数据集 { ( x 1 , y 1 ) , . . , ( x n , y n ) } \{(x_1,y_1),..,(x_n,y_n)\} {(x1,y1),..,(xn,yn)},并假设 ∑ i = 1 n x i = 0 \sum^n_{i=1}x_i=0 ∑i=1nxi=0(做了中心化处理),考虑最简单的线性回归模型
中心化: x ‾ = 1 n ∑ i = 1 n x i x i ′ = x i − x ‾ \overline{x}=\frac{1}{n}\sum^n_{i=1}x_i\qquad x_i'=x_i-\overline{x} x=n1∑i=1nxixi′=xi−x
其中 β 为 权 重 向 量 , β 0 为 偏 置 向 量 \pmb\beta 为权重向量,\beta_0为偏置向量 βββ为权重向量,β0为偏置向量
当使用正规方程求解时,得到
证明如下:
设 C = ∑ i = 1 n ( y i − β T x i ) 2 − 2 β 0 ∑ i = 1 n ( y i − β T x i ) + n β 0 2 则 ∂ C ∂ β 0 = − 2 ∑ i = 1 n y i + 2 β ∑ i = 1 n x i + 2 n β 0 = 0 由 于 x i 已 经 中 心 化 处 理 过 , 所 以 β 0 = 1 n ∑ i = 1 n y i 由 于 X = [ x 1 T . . . x n T ] ∂ C ∂ β = ∂ ∣ ∣ y − X β ∣ ∣ 2 ∂ β 用 之 前 求 解 正 规 方 程 的 方 法 即 可 得 到 解 \begin{aligned} &设C=\sum_{i=1}^n(y_i-\beta^Tx_i)^2-2\beta_0\sum_{i=1}^n(y_i-\beta^Tx_i)+n\beta_0^2&&\\ &则\frac{\partial C}{\partial \beta_0}=-2\sum^n_{i=1}y_i+2\pmb{\beta}\sum_{i=1}^nx_i+2n\beta_0=0\\ &由于x_i已经中心化处理过,所以\beta_0=\frac{1}{n}\sum_{i=1}^ny_i\\ &由于\pmb{X}=\begin{bmatrix} \pmb x_1^T\\...\\ \pmb x_n^T \end{bmatrix}\\ &\frac{\partial C}{\partial \pmb{\beta}}=\frac{\partial ||y-\pmb X\pmb \beta||^2}{\partial \pmb{\beta}}\\ &用之前求解正规方程的方法即可得到解 \end{aligned} 设C=i=1∑n(yi−βTxi)2−2β0i=1∑n(yi−βTxi)+nβ02则∂β0∂C=−2i=1∑nyi+2βββi=1∑nxi+2nβ0=0由于xi已经中心化处理过,所以β0=n1i=1∑nyi由于XXX=⎣⎡xxx1T...xxxnT⎦⎤∂βββ∂C=∂βββ∂∣∣y−XXXβββ∣∣2用之前求解正规方程的方法即可得到解
当 n ≪ p n\ll p n≪p时,很容易导致解病态、陷入过拟合
为了缓解过拟合,为误差函数增加惩罚项
L2正则化——岭回归
当q=2时,即使用L2范数正则化(称为ridge regression,岭回归)
C = ∣ ∣ X β − y ∣ ∣ 2 + λ ∣ ∣ β ∣ ∣ 2 C=||X\pmb \beta -y||^2+\lambda||\pmb \beta||^2 C=∣∣Xβββ−y∣∣2+λ∣∣βββ∣∣2
解为
β = ( X T X + λ I ) − 1 X T y \pmb{\beta}=(\pmb X^T\pmb X+\lambda \pmb I)^{-1}\pmb X^Ty βββ=(XXXTXXX+λIII)−1XXXTy
C = ∣ ∣ X β − y ∣ ∣ 2 + λ ∣ ∣ β ∣ ∣ 2 = ( X β − y ) T ( X β − y ) + λ β T β = ( β T X T − y T ) ( X β − y ) + λ β T β = β T X T X β − y T X β − β T X T y + y T y + λ β T β 利 用 矩 阵 求 导 公 式 ∂ x T B x ∂ x = ( B + B T ) x ∂ x T a ∂ x = ∂ a T x ∂ x = a 可 得 到 ∂ C ∂ β = 2 X T X β − 2 X T y + 2 λ β = 0 可 得 到 β = ( X T X + λ I ) − 1 X T y \begin{aligned} &C=|| X\beta -y||^2+\lambda||\pmb \beta||^2\\ &\quad=(X\beta -y)^T(X\beta -y)+\lambda\beta^T\beta\\ &\quad=(\beta^TX^T-y^T)(X\beta -y)+\lambda\beta^T\beta\\ &\quad=\beta^TX^T X\beta-y^TX\beta -\beta^T X^Ty+y^Ty+\lambda\beta^T\beta\\ &利用矩阵求导公式\\ &\frac{\partial x^TBx}{\partial x}=(B+B^T)x\\ &\frac{\partial x^Ta}{\partial x}=\frac{\partial a^Tx}{\partial x}=a\\ &可得到\frac{\partial C}{\partial\beta}=2X^TX\beta-2X^Ty+2\lambda\beta=0\\ &可得到\beta=(X^TX+\lambda I)^{-1}X^Ty \end{aligned} C=∣∣Xβ−y∣∣2+λ∣∣βββ∣∣2=(Xβ−y)T(Xβ−y)+λβTβ=(βTXT−yT)(Xβ−y)+λβTβ=βTXTXβ−yTXβ−βTXTy+yTy+λβTβ利用矩阵求导公式∂x∂xTBx=(B+BT)x∂x∂xTa=∂x∂aTx=a可得到∂β∂C=2XTXβ−2XTy+2λβ=0可得到β=(XTX+λI)−1XTy
岭回归等价于
上式更加明显的表示出了的约束条件。可以证明 和 之间 存在一一对应关系
直观对比线性回归和岭回归,可以看到参数进行了缩减
这样能使噪声Δx对实际的β影响较小
β ( x + Δ x ) = β x + β Δ x \beta(x+\Delta x)=\beta x+\beta\Delta x β(x+Δx)=βx+βΔx
q 取不同值时,正则化项的等值线
L1正则化——Lasso回归
L1- 正则化(Least Absolute Shrinkage and Selection Operator, Lasso回归)
与其等价的拉格朗日表达形式
L1约束使得解关于 非线性,而且不能像岭回归那样可以得到封闭解。\
Lasso回归:
以一个特例进行说明
比如,如果原本线性回归的 β j = λ 4 \beta_j=\frac{\lambda}{4} βj=4λ,则利用L1正则化使 β j = 0 \beta_j=0 βj=0
比如,如果原本线性回归的 β j = λ \beta_j=\lambda βj=λ,则利用L1正则化使 β j = λ 2 \beta_j=\frac{\lambda}{2} βj=2λ
比如,如果原本线性回归的 β j = − λ \beta_j=-\lambda βj=−λ,则利用L1正则化使 β j = − λ 2 \beta_j=-\frac{\lambda}{2} βj=−2λ
向中间的0靠拢
这样能使权重矩阵中在 ( − λ 2 , λ 2 ) (-\frac{\lambda}{2},\frac{\lambda}{2}) (−2λ,2λ)的 β \beta β置为0,从而达到特征选择的作用
以上说明,L1正则化模型是一种嵌入式特征选择方法,将学习器和特征选择融为一体
总结
正则化是实现嵌入式特征选择的常用方法
对于一般的学习任务,不希望权重过大
如果权重过大,导致微小的特征变化引起较大的预测变化
倾向于零权重,从而消除与任务无关的特征
参考资料
[1]庞善民.西安交通大学机器学习导论2022春PPT
[2]周志华.机器学习.北京:清华大学出版社,2016
[3]怎样理解 Curse of Dimensionality(维数灾难)?
![[机器学习导论]——第四课——特征选择_第1张图片](http://img.e-com-net.com/image/info8/695cc55c42354e2ea81348afbd02e3a2.jpg)
![[机器学习导论]——第四课——特征选择_第2张图片](http://img.e-com-net.com/image/info8/4eb0a724c27f430b8e0ba8df4dda274b.jpg)
![[机器学习导论]——第四课——特征选择_第3张图片](http://img.e-com-net.com/image/info8/063e0454486043d3b5c1e4bfabd751f5.jpg)
![[机器学习导论]——第四课——特征选择_第4张图片](http://img.e-com-net.com/image/info8/48d522d2fa3d465696ab2ee54fbdee1d.jpg)
![[机器学习导论]——第四课——特征选择_第5张图片](http://img.e-com-net.com/image/info8/6d28eefef8f94748b1f08a84896e0758.jpg)
![[机器学习导论]——第四课——特征选择_第7张图片](http://img.e-com-net.com/image/info8/c7326f5bc2344a538cee63e9dcb2dfa5.jpg)
![[机器学习导论]——第四课——特征选择_第8张图片](http://img.e-com-net.com/image/info8/40c2ac5e1c574f699afd29a12c2e8e6a.jpg)
![[机器学习导论]——第四课——特征选择_第9张图片](http://img.e-com-net.com/image/info8/5f1281e4ae124fd1ae0b6ca4ddec73c4.jpg)
![[机器学习导论]——第四课——特征选择_第10张图片](http://img.e-com-net.com/image/info8/a9875dabf0cc44818744517d49a790bf.jpg)
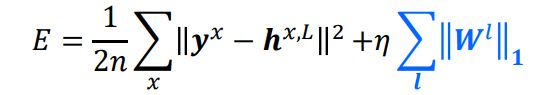
![[机器学习导论]——第四课——特征选择_第11张图片](http://img.e-com-net.com/image/info8/1bd81d9085984f93bd78aa35f4167779.jpg)
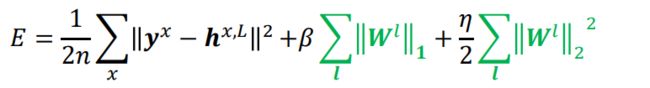
![[机器学习导论]——第四课——特征选择_第12张图片](http://img.e-com-net.com/image/info8/e8d4f7876a634f8d8e0ac0421f7b41d3.jpg)
![[机器学习导论]——第四课——特征选择_第13张图片](http://img.e-com-net.com/image/info8/693069cc4a504e3c9452d3afb59d67cf.jpg)
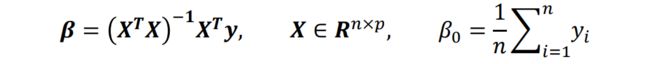
![[机器学习导论]——第四课——特征选择_第14张图片](http://img.e-com-net.com/image/info8/7a5548cc4be24112bb30d6b4bc084be2.jpg)
![[机器学习导论]——第四课——特征选择_第15张图片](http://img.e-com-net.com/image/info8/becf2ba81667446988179de168f4c1db.jpg)
![[机器学习导论]——第四课——特征选择_第16张图片](http://img.e-com-net.com/image/info8/11d0b72e1cdf4678b762f8357d875ca7.jpg)
![[机器学习导论]——第四课——特征选择_第17张图片](http://img.e-com-net.com/image/info8/32d7a922f154468185c1abb9adbe54ef.jpg)
![[机器学习导论]——第四课——特征选择_第18张图片](http://img.e-com-net.com/image/info8/ca17d436fbd94ee58018d5d99e640c39.jpg)
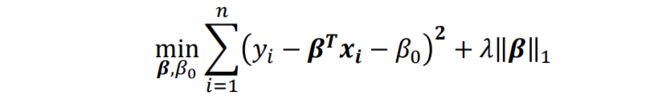
![[机器学习导论]——第四课——特征选择_第19张图片](http://img.e-com-net.com/image/info8/0a28ff2b60064dcb9fe94606532fd2e3.jpg)
![[机器学习导论]——第四课——特征选择_第20张图片](http://img.e-com-net.com/image/info8/656eba890e2b48deb6a4ffe89b8f7270.jpg)