QAM信号的调制解调原理
文章目录
- 1. QAM调节解调系统组成
- 2. 差分编码与星座映射
- 3. QAM调制解调的MATLAB仿真
1. QAM调节解调系统组成
正交振幅调制是利用已调信号在相同带宽内的频谱正交来实现两路并行的数据信息传输,其信道频带利用率与单边带调制一样,主要用于高速数据传输系统中。QAM系统组成框图如下所示。
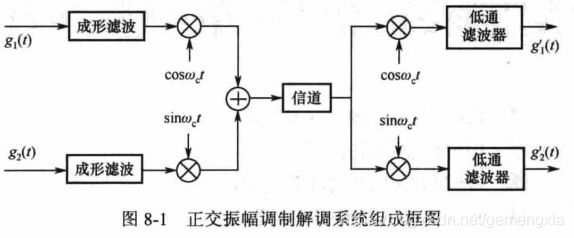
图中 g 1 ( t ) g_{1}(t) g1(t)和 g 2 ( t ) g_{2}(t) g2(t)是两个独立的带宽受限的基带波形, c o s ω c t cos\omega_{c}t cosωct和 s i n ω c t sin\omega_{c}t sinωct是两个相互正交的载波。由上图可知,发送端形成的正交振幅调制信号为
s ( t ) = g 1 ( t ) c o s ω c t + g 2 ( t ) s i n ω c t s(t)=g_{1}(t)cos\omega_{c}t+g_{2}(t)sin\omega_{c}t s(t)=g1(t)cosωct+g2(t)sinωct
若信道具有理想传输特性,则加到解调器输入端的信号也是 s ( t ) s(t) s(t)。假设接收端所产生的的相干载波与发送端完全相同,那么,相互正交的两路解调器的输出分别为
m 1 ( t ) = [ g 1 ( t ) c o s ω c t + g 2 ( t ) s i n ω c t ] c o s ω c t = 1 2 g 1 ( t ) + 1 2 [ g 1 ( t ) c o s 2 ω c t + g 2 ( t ) s i n 2 ω c t ] m_{1}(t)=[g_{1}(t)cos\omega_{c}t+g_{2}(t)sin\omega_{c}t]cos\omega_{c}t=\frac{1}{2}g_{1}(t)+\frac{1}{2}[g_{1}(t)cos2\omega_{c}t+g_{2}(t)sin2\omega_{c}t] m1(t)=[g1(t)cosωct+g2(t)sinωct]cosωct=21g1(t)+21[g1(t)cos2ωct+g2(t)sin2ωct]
m 2 ( t ) = [ g 1 ( t ) c o s ω c t + g 2 ( t ) s i n ω c t ] s i n ω c t = 1 2 g 2 ( t ) + 1 2 [ g 1 ( t ) s i n 2 ω c t − g 2 ( t ) c o s 2 ω c t ] m_{2}(t)=[g_{1}(t)cos\omega_{c}t+g_{2}(t)sin\omega_{c}t]sin\omega_{c}t=\frac{1}{2}g_{2}(t)+\frac{1}{2}[g_{1}(t)sin2\omega_{c}t-g_{2}(t)cos2\omega_{c}t] m2(t)=[g1(t)cosωct+g2(t)sinωct]sinωct=21g2(t)+21[g1(t)sin2ωct−g2(t)cos2ωct]
经低通滤波后,上、下两支路输出的基带波形分别为
g 1 ′ ( t ) = 1 2 g 1 ( t ) , g 2 ′ ( t ) = 1 2 g 2 ( t ) {g_{1}}'(t)=\frac{1}{2}g_{1}(t),{g_{2}}'(t)=\frac{1}{2}g_{2}(t) g1′(t)=21g1(t),g2′(t)=21g2(t)
这样,就无失真地完成了基带波形的传输。
需要说明的是,在正交振幅调制系统中,当接收端恢复出的载波与接收信号中的载波存在相位误差 Δ φ \Delta \varphi Δφ时,不但单个解调支路的期望信号分量的功率减少 c o s 2 Δ φ cos^{2}\Delta \varphi cos2Δφ,而且在同相和正交分量之间还存在交互干扰。由于同相及正交两支路信号的平均功率电平相似,一个较小的相位误差就会引起性能较大下降,因此,QAM信号对恢复出的相干载波信号的相位稳态误差要求比其他调制方式更高。
对于QAM调制方式来讲,若输入的基带信号为多电平时,即可构成多电平正交振幅调制,如16QAM、64QAM等。我们比较一下QAM信号的时域表达式与QPSK调制信号,可以看出,QAM信号的基带波形取两种电平( ± 1 \pm 1 ±1)时,正好与QPSK调制信号完全相同。在实际的工程应用中,为了获得较高的频带利用率,QAM通常采用 M ( M > 4 ) M(M> 4) M(M>4)进制调制方式,如基带信号为4种电平的16QAM、6种电平的64QAM、8种电平的256QAM,甚至更高阶的QAM调制系统。
2. 差分编码与星座映射
通信系统中通常把信号矢量端点的分布图称为星座图。同基带数字传输的眼图相比较,星座图可以看成数字信号的一个二维眼图阵列,同时符号在图中所处的位置具有合理的限制或判决边界。代表各接收符号的点在图中越接近,信号质量就越高。由于屏幕上的图形对应着幅度和相位,阵列的形状可用来分析和确定系统或信道的许多缺陷和畸变,并帮助查找其原因。使用星座图可以轻松发现诸如幅度噪声、相位噪声、相位误差、调制误差比等调制问题。
由于已调信号的振幅和相位均有不同的取值,因而其信号星座图的结构形状可以有许多种,如圆形、三角形、矩形、六角形等。下图为16QAM的方形星座图、圆形星座图和16PSK信号的星座图。
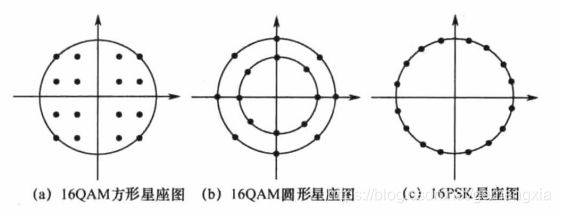
由图可见,在进制数(M)相同的条件下,星座图的结构不同时,各信号点之间的最小距离也不同,因而相应的调制方式也会具有不同的误码性能,且最小距离越大,其误码性能越好。容易证明,对于上图中的三种星座图来讲,当各信号之间的最小距离相同时,方形16QAM星座图比星形结构的平均功率小1.5dB,比16PSK小2.55dB。
可以将上述公式中的 g 1 ( t ) 、 g 2 ( t ) g_{1}(t)、g_{2}(t) g1(t)、g2(t)看做星座图中的横坐标和纵坐标。对于16QAM来说,每个基带波形需要用2bit二进制数据来表示,横坐标及纵坐标共组成4bit二进制数据。也就是说,星座图中的每个信号点可由4bit二进制数据表示。对于16QAM来说,每个符号携带了4bit信息,每个符号可能有16中状态,每种状态由载波的幅度和相位信息共同确定。
所谓发射端的信息编码,也就是需要将输入的符号信号(4bit二进制信息)映射成上图(a)中的横坐标及纵坐标,而后采用图8-1所示的结构进行调制。接收端的信息解码,则需要在完成载波相干解调后,根据正交两路的基带波形判决出的值,根据发射端的编码规则,还原成原始的调制信息。这里其实涉及两个问题:一是由于QAM通常采用相干解调,在接收端恢复相干载波时,不可避免地存在四相相位模糊问题;二是根据信息检测理论,对多电平信号进行检测并恢复成二进制码时,格雷码比自然码具有更好的误码性能,因此编码时需要采用格雷码编码技术。
QAM信号的差分编码可以分为全部差分编码和部分差分编码。所谓全部差分编码,是指将表示每个符号的所有二进制序列均需要进行差分编码,其实现难度及所需资源较大,特别是对于高阶QAM的调制系统,其所需资源就更大了;而部分差分编码只对每个符号的前两个比特进行差分编码,不仅可以减少资源消耗,而且由于减少了差分编码的比特数,因而减少了因差分编码带来的误码扩散。需要说明的是,在部分编码中,前两个比特用来规定信号所处的象限,并对其进行差分编码;余下的比特用来规定每个象限中信号矢量的位置,从而克服相干解调带来的四相模糊问题。
差分编码的模4格雷加法器公式为
I k = [ ( A k ⊕ B k ‾ ) ⋅ ( A k ⊕ I k − 1 ) ] ⊕ [ ( A k ⊕ B k ) ⋅ ( A k ⊕ Q k − 1 ) ] I_{k}=[(\overline{A_{k}\oplus B_{k}})\cdot (A_{k}\oplus I_{k-1})]\oplus [(A_{k}\oplus B_{k})\cdot (A_{k}\oplus Q_{k-1})] Ik=[(Ak⊕Bk)⋅(Ak⊕Ik−1)]⊕[(Ak⊕Bk)⋅(Ak⊕Qk−1)]
Q k = [ ( A k ⊕ B k ‾ ) ⋅ ( A k ⊕ Q k − 1 ) ] ⊕ [ ( A k ⊕ B k ) ⋅ ( A k ⊕ I k − 1 ) ] Q_{k}=[(\overline{A_{k}\oplus B_{k}})\cdot (A_{k}\oplus Q_{k-1})]\oplus [(A_{k}\oplus B_{k})\cdot (A_{k}\oplus I_{k-1})] Qk=[(Ak⊕Bk)⋅(Ak⊕Qk−1)]⊕[(Ak⊕Bk)⋅(Ak⊕Ik−1)]
差分编码的模4格雷加法器公式为
A k = [ ( I k ⊕ Q k ‾ ) ⋅ ( I k ⊕ Q k − 1 ) ] ⊕ [ ( I k ⊕ Q k ) ⋅ ( I k ⊕ I k − 1 ) ] A_{k}=[(\overline{I_{k}\oplus Q_{k}})\cdot (I_{k}\oplus Q_{k-1})]\oplus [(I_{k}\oplus Q_{k})\cdot (I_{k}\oplus I_{k-1})] Ak=[(Ik⊕Qk)⋅(Ik⊕Qk−1)]⊕[(Ik⊕Qk)⋅(Ik⊕Ik−1)]
B k = [ ( I k ⊕ Q k ‾ ) ⋅ ( Q k ⊕ I k − 1 ) ] ⊕ [ ( I k ⊕ Q k ) ⋅ ( Q k ⊕ Q k − 1 ) ] B_{k}=[(\overline{I_{k}\oplus Q_{k}})\cdot (Q_{k}\oplus I_{k-1})]\oplus [(I_{k}\oplus Q_{k})\cdot (Q_{k}\oplus Q_{k-1})] Bk=[(Ik⊕Qk)⋅(Qk⊕Ik−1)]⊕[(Ik⊕Qk)⋅(Qk⊕Qk−1)]
式中, A k 、 B k A_{k}、B_{k} Ak、Bk为差分编码前的数据, I k 、 Q k I_{k}、Q_{k} Ik、Qk为差分编码后的数据, ⊕ \oplus ⊕为模2加(逻辑异或)。
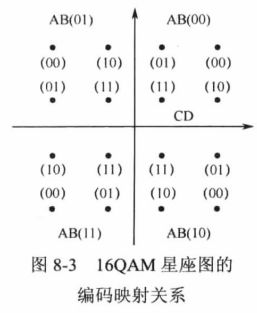
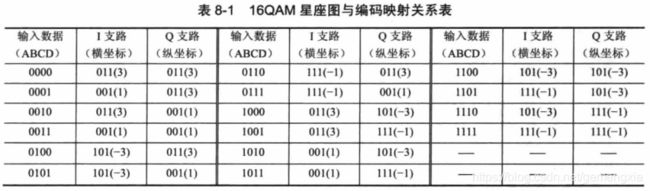
上图为具有旋转关系的16QAM星座图。横坐标及纵坐标的取均值只有4种,且分别为 ± 1 、 ± 3 \pm 1、\pm3 ±1、±3,每种坐标值需要3bit二进制来表示,其中,1对应的二进制为001,-1对应的二进制数为111,3对应的二进制数为011,-3对应的二进制数为101,。根据以上的讨论,可以得出经差分编码后输入的符号(4bit二进制数据)与QAM调制系统中的I、Q支路 g 1 ( t ) 、 g 2 ( t ) g_{1}(t)、g_{2}(t) g1(t)、g2(t)映射关系,如下表所示。
3. QAM调制解调的MATLAB仿真
条件:仿真4bit原始数据与星座图的编码映射过程;完成16QAM信号的调制解调;基带信号符号速率 R b = 1 M b p s R_{b}=1Mbps Rb=1Mbps;成形滤波器的滚将因子 α = 0.8 \alpha=0.8 α=0.8;载波信号频率 f c = 2 M H z f_{c}=2MHz fc=2MHz;采样频率 f c = 8 R b f_{c}=8R_{b} fc=8Rb;
产生16进制随机数据,而后将其转换成4bit二进制数据,并对高位的2bit进行差分编码;将编码后的2bit数据与其余2bit重新组合成4bit数据后,完成星座图映射,再将映射后的I/Q支路信号经成形滤波器,再与正余弦载波信号完成乘加运算,即产生16QAM调制信号。
解调时,只需将调制信号分别于同相正交的相干载波相乘,并匹配滤波输出,即可获得同相正交支路的基带波形。
源码:
clc;
ps=1*10^6; %码速率为1MHz
a=0.8; %成形滤波器系数
Fs=8*10^6; %采样速率
fc=2*10^6; %载波频率
N=50000; %仿真数据的长度
t=0:1/Fs:(N*Fs/ps-1)/Fs;%产生长度为N,频率为fs的时间序列
s=randint(N,1,16); %产生随机16进制数据作为原始数据
Bs=dec2bin(s,4); %将十进制数据转换成4比特的二进制数据
%对Bs的高2比特进行差分编码
%取高2比特分别存放在A,B变量中
A=s>7;
B=(s-A*8)>3;
%差分编码后的数据存放在C,D中
C=zeros(N,1);D=zeros(N,1);
for i=2:N
C(i)=mod(((~mod(A(i)+B(i),2))&mod(A(i)+C(i-1),2)) + (mod(A(i)+B(i),2)&mod(A(i)+D(i-1),2)),2);
D(i)=mod(((~mod(A(i)+B(i),2))&mod(B(i)+D(i-1),2)) + (mod(A(i)+B(i),2)&mod(B(i)+C(i-1),2)),2);
end
%差分编码后的高2比特数据与原数据低2比特合成映射前的数据DBs
DBs=C*8+D*4+s-A*8-B*4;
%完成调制前的正交同相支路数据映射
I=zeros(1,N);Q=zeros(1,N);
for i=1:N
switch DBs(i)
case 0, I(i)=3; Q(i)=3;
case 1, I(i)=1; Q(i)=3;
case 2, I(i)=3; Q(i)=1;
case 3, I(i)=1; Q(i)=1;
case 4, I(i)=-3;Q(i)=3;
case 5, I(i)=-3;Q(i)=1;
case 6, I(i)=-1;Q(i)=3;
case 7, I(i)=-1;Q(i)=1;
case 8, I(i)=3; Q(i)=-3;
case 9, I(i)=3; Q(i)=-1;
case 10,I(i)=1; Q(i)=-3;
case 11,I(i)=1; Q(i)=-1;
case 12,I(i)=-3;Q(i)=-3;
case 13,I(i)=-1;Q(i)=-3;
case 14,I(i)=-3;Q(i)=-1;
otherwise,I(i)=-1;Q(i)=-1;
end
end
%对编码数据以Fs频率采样
Ads_i=upsample(I,Fs/ps);
Ads_q=upsample(Q,Fs/ps);
%加噪声
% SNR=30;
% Ads_i=awgn(Ads_i,SNR);
% Ads_q=awgn(Ads_q,SNR);
%设计平方根升余弦滤波器
n_T=[-2 2];
rate=Fs/ps;
T=1;
Shape_b = rcosfir(a,n_T,rate,T,'sqrt');
%对采样后的数据进行升余弦滤波;
rcos_Ads_i=filter(Shape_b,1,Ads_i);
rcos_Ads_q=filter(Shape_b,1,Ads_q);
%产生同相正交两路载频信号
f0_i=cos(2*pi*fc*t);
f0_q=sin(2*pi*fc*t);
%产生16QAM已调信号
qam16=rcos_Ads_i.*f0_i+rcos_Ads_q.*f0_q;
%实现相干解调
demod_mult_i=qam16.*f0_i;
demod_mult_q=qam16.*f0_q;
%对乘法运算后的同相正交支路滤波
demod=filter(Shape_b,1,demod_mult_i+sqrt(-1)*demod_mult_q);
%绘制相干解调后的星座图
scatterplot(demod,Fs/ps,6*rate,'bx');
%仿真频率差500Hz时解调后星座图
f0_di=cos(2*pi*(fc+500)*t);
f0_dq=sin(2*pi*(fc+500)*t);
%实现解调
demod_mult_i=qam16.*f0_di;
demod_mult_q=qam16.*f0_dq;
%对乘法运算后的同相正交支路滤波
demod=filter(Shape_b,1,demod_mult_i+sqrt(-1)*demod_mult_q);
%绘制解调后的星座图
scatterplot(demod,Fs/ps,6*rate,'bx');
%仿真相位差 pi/6时解调后星座图
f0_di=cos(2*pi*fc*t+pi/6);
f0_dq=sin(2*pi*fc*t+pi/6);
%实现解调
demod_mult_i=qam16.*f0_di;
demod_mult_q=qam16.*f0_dq;
%对乘法运算后的同相正交支路滤波
demod=filter(Shape_b,1,demod_mult_i+sqrt(-1)*demod_mult_q);
%绘制解调后的星座图
scatterplot(demod,Fs/ps,6*rate,'bx');
%绘制16QAM信号频谱、信号时域波形
m_qam16=20*log10(abs(fft(qam16,1024)));m_qam16=m_qam16-max(m_qam16);
%设置幅频响应的横坐标单位为MHz
x_f=[0:(Fs/length(m_qam16)):Fs/2];x_f=x_f/10^6;
%只显示正频率部分的幅频响应
mqam16=m_qam16(1:length(x_f));
%设置时域波表的横坐标单位为us
Len=100;%设置时域波形显示的点数
x_t=1:Len;%产生长度为Len的时间序列
x_t=x_t/Fs*10^6;
%显示所需的频谱及时域波形
subplot(211); plot(x_f,mqam16);
legend('16QAM信号频谱');
xlabel('频率(MHz)');ylabel('幅度(dB)');grid on;
subplot(212);plot(x_t,qam16(101:Len+100));
legend('16QAM时域信号波形');
xlabel('时间(us)');ylabel('幅度(V)');grid on;
仿真结果
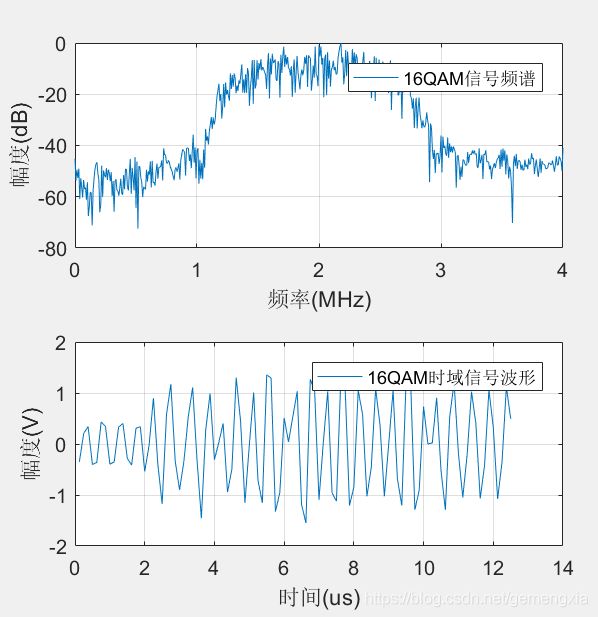
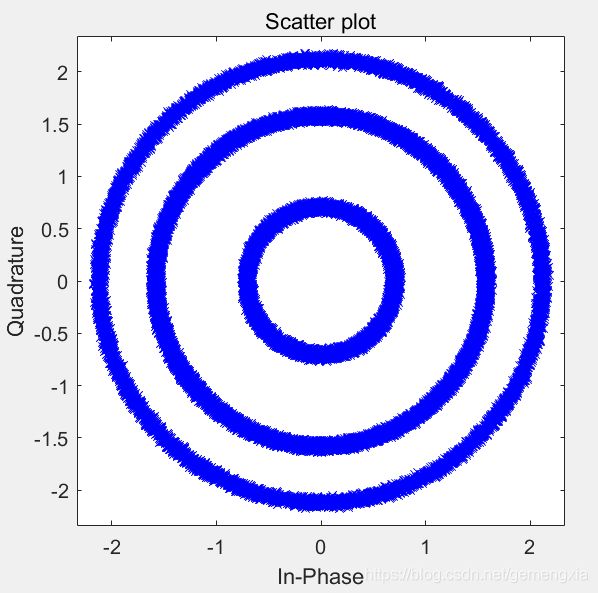
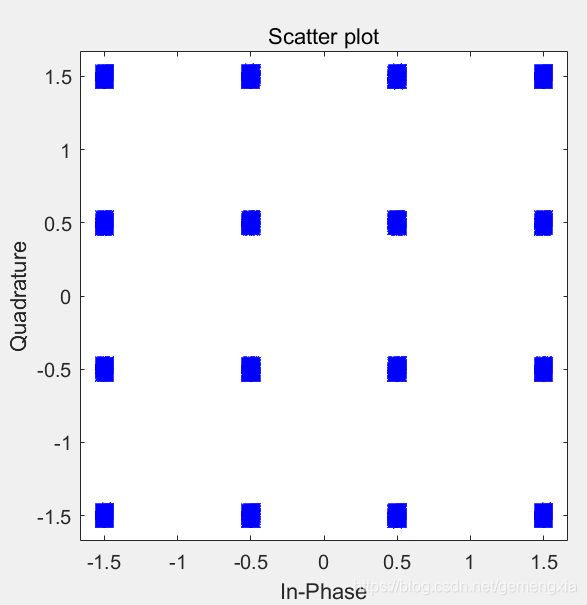
从图中可以看出,相干解调后星座图的形状成方形,且每个符号点信号集中程度好;解调后的星座图呈现三个同心圆的形状,主要是各信号的幅度其实只有3种状态,频率的变化实质上也会体现在相位的变化上,当频差固定时,相差会遍历360°,因为呈现出三个同心圆的形状。