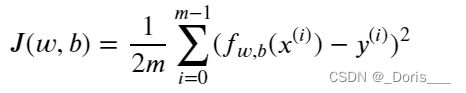监督学习week 1: 单变量线性回归optional_lab收获记录
目录
1.cost function
2.gradient&gradient descent
①compute_gradient
②Gradient Descent
③使用:
④画图&预测
1.cost function
#Function to calculate the cost
def compute_cost(x, y, w, b):
m = x.shape[0]
cost = 0
for i in range(m):
f_wb = w * x[i] + b
cost = cost + (f_wb - y[i])**2
total_cost = 1 / (2 * m) * cost
return total_cost2.gradient&gradient descent
①compute_gradient
def compute_gradient(x, y, w, b):
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x[i] + b
dj_dw_i = (f_wb - y[i]) * x[i]
dj_db_i = f_wb - y[i]
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db②Gradient Descent
def gradient_descent(x, y, w_in, b_in, alpha, num_iters,
cost_function, gradient_function):
w = copy.deepcopy(w_in) # avoid modifying global w_in
# An array to store cost J and w's at each iteration primarily for graphing later
J_history = []
p_history = []
b = b_in
w = w_in
for i in range(num_iters):
# Calculate the gradient and update the parameters using gradient_function
dj_dw, dj_db = gradient_function(x, y, w , b)
# Update Parameters using equation (3) above
b = b - alpha * dj_db
w = w - alpha * dj_dw
# Save cost J at each iteration
if i<100000: # prevent resource exhaustion
J_history.append( cost_function(x, y, w , b))
p_history.append([w,b])
# Print cost every at intervals 10 times or as many iterations if < 10
if i% math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",
f"w: {w: 0.3e}, b:{b: 0.5e}")
return w, b, J_history, p_history #return w and J,w history for graphing注意:函数的参数调用其他函数(本质上,也是一个对象->可以当做参数使用)
③使用:
# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist =
gradient_descent(x_train ,y_train, w_init, b_init,
tmp_alpha, iterations, compute_cost, compute_gradient)
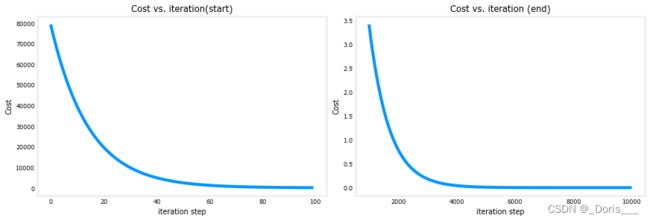
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")④画图&预测
# plot cost versus iteration
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)"); ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost') ; ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step') ; ax2.set_xlabel('iteration step')
plt.show()